diff options
| author | Yuren Hao <yurenh2@timan108.cs.illinois.edu> | 2025-09-04 22:16:22 -0500 |
|---|---|---|
| committer | Yuren Hao <yurenh2@timan108.cs.illinois.edu> | 2025-09-04 22:16:22 -0500 |
| commit | fc6d57ffb8d5ddb5820fcc00b5491a585c259ebc (patch) | |
| tree | e9841f93a353e2107225cfc721d1ce57c0e594dc /Qwen2.5-Eval/evaluation/latex2sympy | |
Initial commit
Diffstat (limited to 'Qwen2.5-Eval/evaluation/latex2sympy')
66 files changed, 14809 insertions, 0 deletions
diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/.coveragerc b/Qwen2.5-Eval/evaluation/latex2sympy/.coveragerc new file mode 100755 index 0000000..3aeb83f --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/.coveragerc @@ -0,0 +1,31 @@ +# .coveragerc to control coverage.py +[run] +branch = True +include = + latex2sympy.py +omit = + sandbox/* + gen/* + asciimath_printer.py + setup.py + __init__.py + +[report] +# Regexes for lines to exclude from consideration +exclude_lines = + # Have to re-enable the standard pragma + pragma: no cover + + # Don't complain about missing debug-only code: + def __repr__ + if self\.debug + + # Don't complain if tests don't hit defensive assertion code: + raise AssertionError + raise NotImplementedError + + # Don't complain if non-runnable code isn't run: + if 0: + if __name__ == .__main__.: + +ignore_errors = True diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/.gitignore b/Qwen2.5-Eval/evaluation/latex2sympy/.gitignore new file mode 100755 index 0000000..e49e834 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/.gitignore @@ -0,0 +1,132 @@ +# Byte-compiled / optimized / DLL files +__pycache__/ +*.py[cod] +*$py.class +.antlr + +# C extensions +*.so + +# Distribution / packaging +.Python +build/ +develop-eggs/ +dist/ +downloads/ +eggs/ +.eggs/ +lib/ +lib64/ +parts/ +sdist/ +var/ +wheels/ +pip-wheel-metadata/ +share/python-wheels/ +*.egg-info/ +.installed.cfg +*.egg +MANIFEST + +# PyInstaller +# Usually these files are written by a python script from a template +# before PyInstaller builds the exe, so as to inject date/other infos into it. +*.manifest +*.spec + +# Installer logs +pip-log.txt +pip-delete-this-directory.txt + +# Unit test / coverage reports +htmlcov/ +.tox/ +.nox/ +.coverage +.coverage.* +.cache +nosetests.xml +coverage.xml +*.cover +.hypothesis/ +.pytest_cache/ + +# Translations +*.mo +*.pot + +# Django stuff: +*.log +local_settings.py +db.sqlite3 + +# Flask stuff: +instance/ +.webassets-cache + +# Scrapy stuff: +.scrapy + +# Sphinx documentation +docs/_build/ + +# PyBuilder +target/ + +# Jupyter Notebook +.ipynb_checkpoints + +# IPython +profile_default/ +ipython_config.py + +# pyenv +.python-version + +# pipenv +# According to pypa/pipenv#598, it is recommended to include Pipfile.lock in version control. +# However, in case of collaboration, if having platform-specific dependencies or dependencies +# having no cross-platform support, pipenv may install dependencies that don’t work, or not +# install all needed dependencies. +#Pipfile.lock + +# celery beat schedule file +celerybeat-schedule + +# SageMath parsed files +*.sage.py + +# Environments +.env +.venv +env/ +venv/ +ENV/ +env.bak/ +venv.bak/ + +# Spyder project settings +.spyderproject +.spyproject + +# Rope project settings +.ropeproject + +# mkdocs documentation +/site + +# mypy +.mypy_cache/ +.dmypy.json +dmypy.json + +# Pyre type checker +.pyre/ + +# Azure Functions artifacts +bin +obj +appsettings.json +local.settings.json +.python_packages +stemgen-solution-engine.zip
\ No newline at end of file diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/LICENSE.txt b/Qwen2.5-Eval/evaluation/latex2sympy/LICENSE.txt new file mode 100755 index 0000000..6bbfda9 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/LICENSE.txt @@ -0,0 +1,21 @@ +The MIT License (MIT) + +Copyright 2016, latex2sympy + +Permission is hereby granted, free of charge, to any person obtaining a copy +of this software and associated documentation files (the "Software"), to deal +in the Software without restriction, including without limitation the rights +to use, copy, modify, merge, publish, distribute, sublicense, and/or sell +copies of the Software, and to permit persons to whom the Software is +furnished to do so, subject to the following conditions: + +The above copyright notice and this permission notice shall be included in all +copies or substantial portions of the Software. + +THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR +IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, +FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE +AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER +LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, +OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE +SOFTWARE. diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/PS.g4 b/Qwen2.5-Eval/evaluation/latex2sympy/PS.g4 new file mode 100755 index 0000000..51834a2 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/PS.g4 @@ -0,0 +1,638 @@ +grammar PS; + +options { + language=Python2; +} + +WS: [ \t\r\n]+ -> skip; +DOLLAR_SIGN: '\\$' -> skip; + +ADD: '+'; +SUB: '-'; +MUL: '*'; +DIV: '/' | '\\over'; + +L_PAREN: '('; +R_PAREN: ')'; +L_GROUP: '\\lgroup'; +R_GROUP: '\\rgroup'; +L_BRACE: '{'; +R_BRACE: '}'; +L_BRACE_VISUAL: '\\{'; +R_BRACE_VISUAL: '\\}'; +L_BRACE_CMD: '\\lbrace'; +R_BRACE_CMD: '\\rbrace'; +L_BRACKET: '['; +R_BRACKET: ']'; +L_BRACK: '\\lbrack'; +R_BRACK: '\\rbrack'; + +BAR: '|'; +L_VERT: '\\lvert'; +R_VERT: '\\rvert'; +VERT: '\\vert'; + +NORM: '\\|'; + +L_FLOOR: '\\lfloor'; +R_FLOOR: '\\rfloor'; +LL_CORNER: '\\llcorner'; +LR_CORNER: '\\lrcorner'; + +L_CEIL: '\\lceil'; +R_CEIL: '\\rceil'; +UL_CORNER: '\\ulcorner'; +UR_CORNER: '\\urcorner'; + +L_LEFT: '\\left'; +R_RIGHT: '\\right'; +ML_LEFT: '\\mleft'; +MR_RIGHT: '\\mright'; + +//functions +FUNC_LIM: '\\lim'; +LIM_APPROACH_SYM: '\\to' | '\\rightarrow' | '\\Rightarrow' | '\\longrightarrow' | '\\Longrightarrow'; +FUNC_INT: '\\int'; +FUNC_SUM: '\\sum'; +FUNC_PROD: '\\prod'; + +FUNC_LOG: '\\log'; +FUNC_LN: '\\ln'; +FUNC_EXP: '\\exp'; +FUNC_SIN: '\\sin'; +FUNC_COS: '\\cos'; +FUNC_TAN: '\\tan'; +FUNC_CSC: '\\csc'; +FUNC_SEC: '\\sec'; +FUNC_COT: '\\cot'; + +FUNC_ARCSIN: '\\arcsin'; +FUNC_ARCCOS: '\\arccos'; +FUNC_ARCTAN: '\\arctan'; +FUNC_ARCCSC: '\\arccsc'; +FUNC_ARCSEC: '\\arcsec'; +FUNC_ARCCOT: '\\arccot'; + +FUNC_SINH: '\\sinh'; +FUNC_COSH: '\\cosh'; +FUNC_TANH: '\\tanh'; +FUNC_ARSINH: '\\arsinh'; +FUNC_ARCOSH: '\\arcosh'; +FUNC_ARTANH: '\\artanh'; +FUNC_ARCSINH: '\\arcsinh'; +FUNC_ARCCOSH: '\\arccosh'; +FUNC_ARCTANH: '\\arctanh'; + +FUNC_ARSINH_NAME: 'arsinh'; +FUNC_ARCSINH_NAME: 'arcsinh'; +FUNC_ARCOSH_NAME: 'arcosh'; +FUNC_ARCCOSH_NAME: 'arccosh'; +FUNC_ARTANH_NAME: 'artanh'; +FUNC_ARCTANH_NAME: 'arctanh'; +FUNC_GCD_NAME: 'gcd'; +FUNC_LCM_NAME: 'lcm'; +FUNC_FLOOR_NAME: 'floor'; +FUNC_CEIL_NAME: 'ceil'; + +FUNC_SQRT: '\\sqrt'; +FUNC_GCD: '\\gcd'; +FUNC_LCM: '\\lcm'; +FUNC_FLOOR: '\\floor'; +FUNC_CEIL: '\\ceil'; +FUNC_MAX: '\\max'; +FUNC_MIN: '\\min'; + +FUNC_DET: '\\det'; + +FUNC_EYE_NAME: 'eye'; +FUNC_ZEROS_NAME: 'zeros'; +FUNC_ONES_NAME: 'ones'; +FUNC_COLS_NAME: 'cols'; +FUNC_ROWS_NAME: 'rows'; +FUNC_DIAG_NAME: 'diag'; +FUNC_NORM_NAME: 'norm'; +FUNC_RANK_NAME: 'rank'; +FUNC_TRACE_NAME: 'trace' | 'tr'; +FUNC_RREF_NAME: 'rref'; +FUNC_HSTACK_NAME: 'hstack'; +FUNC_VSTACK_NAME: 'vstack'; +FUNC_ORTHOGONALIZE_NAME: 'orth' | 'ortho' | 'orthogonal' | 'orthogonalize'; +FUNC_NULLSPACE_NAME: 'nullspace'; +FUNC_DIAGONALIZE_NAME: 'eig' | 'eigen' | 'diagonalize'; +FUNC_EIGENVALS_NAME: 'eigenvals' | 'eigenvalues'; +FUNC_EIGENVECTORS_NAME: 'eigenvects' | 'eigenvectors'; +FUNC_SVD_NAME: 'svd' | 'SVD'; + +//commands +CMD_TIMES: '\\times'; +CMD_CDOT: '\\cdot'; +CMD_DIV: '\\div'; +CMD_FRAC: '\\frac'; +CMD_BINOM: '\\binom' | '\\tbinom' | '\\dbinom'; +CMD_CHOOSE: '\\choose'; +CMD_MOD: '\\mod'; + +CMD_MATHIT: '\\mathit'; + +CMD_OPERATORNAME: '\\operatorname'; + +//matrix test +MATRIX_TYPE_MATRIX: 'matrix'; +MATRIX_TYPE_PMATRIX: 'pmatrix'; +MATRIX_TYPE_BMATRIX: 'bmatrix'; +MATRIX_TYPE_DET: 'vmatrix'; +MATRIX_TYPES: MATRIX_TYPE_MATRIX | MATRIX_TYPE_PMATRIX | MATRIX_TYPE_BMATRIX; +CMD_MATRIX_START: '\\begin' L_BRACE MATRIX_TYPES R_BRACE; +CMD_MATRIX_END: '\\end' L_BRACE MATRIX_TYPES R_BRACE; +CMD_DET_START: '\\begin' L_BRACE MATRIX_TYPE_DET R_BRACE; +CMD_DET_END: '\\end' L_BRACE MATRIX_TYPE_DET R_BRACE; +MATRIX_DEL_COL: '&'; +MATRIX_DEL_ROW: '\\\\'; + +UNDERSCORE: '_'; +CARET: '^'; +COLON: ':'; +SEMICOLON: ';'; +COMMA: ','; +PERIOD: '.'; + +fragment WS_CHAR: [ \t\r\n]; +DIFFERENTIAL: 'd' WS_CHAR*? ([a-zA-Z] | '\\' [a-zA-Z]+); + +EXP_E: 'e' | '\\exponentialE'; +E_NOTATION_E: 'E'; +LETTER_NO_E: [a-df-zA-DF-Z]; // exclude e for exponential function and e notation +fragment LETTER: [a-zA-Z]; +fragment DIGIT: [0-9]; + +MATRIX_XRIGHTARROW: '\\xrightarrow' | '\\xRightarrow'; +TRANSFORM_EXCHANGE: '<->' | '<=>' | '\\leftrightarrow' | '\\Leftrightarrow'; + +NUMBER: + DIGIT+ (COMMA DIGIT DIGIT DIGIT)* + | DIGIT* (COMMA DIGIT DIGIT DIGIT)* PERIOD DIGIT+; + +E_NOTATION: NUMBER E_NOTATION_E (SUB | ADD)? DIGIT+; + +IN: '\\in'; +ASSIGNMENT: '='; +EQUAL: '==' | '\\equiv'; +LT: '<'; +LTE: '\\leq' | '\\le' | '\\leqslant'; +GT: '>'; +GTE: '\\geq' | '\\ge' | '\\geqslant'; +UNEQUAL: '!=' | '!==' | '\\ne' | '\\neq' | '\\not\\equiv'; + +BANG: '!'; + +fragment PERCENT_SIGN: '\\%'; +PERCENT_NUMBER: NUMBER PERCENT_SIGN; + +//Excludes some letters for use as e.g. constants in SYMBOL +fragment GREEK_LETTER: + '\\char"000391' | //Alpha + '\\alpha' | + '\\char"000392' | //Beta + '\\beta' | + '\\Gamma' | + '\\gamma' | + '\\Delta' | + '\\delta' | + '\\char"000190' | //Epsilon + '\\epsilon' | + '\\varepsilon' | + '\\char"000396' | //Zeta + '\\zeta' | + '\\char"000397' | //Eta + '\\eta' | + '\\Theta' | + '\\theta' | + '\\vartheta' | + '\\char"000399' | //Iota + '\\iota' | + '\\char"00039A' | //Kappa + '\\kappa' | + '\\Lambda' | + '\\lambda' | + '\\char"00039C' | //Mu + '\\mu' | + '\\char"00039D' | //Nu + '\\nu' | + '\\Xi' | + '\\xi' | + '\\char"00039F' | //Omicron + '\\omicron' | + '\\Pi' | + '\\varpi' | + '\\char"0003A1' | //Rho + '\\rho' | + '\\varrho' | + '\\Sigma' | + '\\sigma' | + '\\varsigma' | + '\\char"0003A4' | //Tau + '\\tau' | + '\\Upsilon' | + '\\upsilon' | + '\\Phi' | + '\\phi' | + '\\varphi' | + '\\char"0003A7' | //Chi + '\\chi' | + '\\Psi' | + '\\psi' | + '\\Omega' | + '\\omega'; + +GREEK_CMD: GREEK_LETTER [ ]?; + +fragment OTHER_SYMBOL: + '\\Bbbk' | + '\\wp' | + '\\nabla' | + '\\bigstar' | + '\\angle' | + '\\nexists' | + '\\diagdown' | + '\\measuredangle' | + '\\eth' | + '\\emptyset' | + '\\diagup' | + '\\sphericalangle' | + '\\clubsuit' | + '\\varnothing' | + '\\Diamond' | + '\\complement' | + '\\diamondsuit' | + '\\imath' | + '\\Finv' | + '\\triangledown' | + '\\heartsuit' | + '\\jmath' | + '\\Game' | + '\\triangle' | + '\\spadesuit' | + '\\ell' | + '\\hbar' | + '\\vartriangle' | + '\\hslash' | + '\\blacklozenge' | + '\\lozenge' | + '\\blacksquare' | + '\\mho' | + '\\blacktriangle' | + '\\sharp' | + '\\prime' | + '\\Im' | + '\\flat' | + '\\square' | + '\\backprime' | + '\\Re' | + '\\natural' | + '\\surd' | + '\\circledS'; +OTHER_SYMBOL_CMD: OTHER_SYMBOL [ ]?; + +fragment PI: '\\pi'; +fragment INFTY_CMD: '\\infty'; +fragment PARTIAL_CMD: '\\partial'; +fragment INFTY: INFTY_CMD | DOLLAR_SIGN INFTY_CMD | INFTY_CMD PERCENT_SIGN; +fragment EMPTYSET: '\\emptyset'; +SYMBOL: PI | PARTIAL_CMD | INFTY | EMPTYSET; + +fragment VARIABLE_CMD: '\\variable'; +fragment VARIABLE_SYMBOL: (GREEK_CMD | OTHER_SYMBOL_CMD | LETTER | DIGIT)+ (UNDERSCORE ((L_BRACE (GREEK_CMD | OTHER_SYMBOL_CMD | LETTER | DIGIT | COMMA)+ R_BRACE) | (GREEK_CMD | OTHER_SYMBOL_CMD | LETTER | DIGIT)))?; +VARIABLE: VARIABLE_CMD L_BRACE VARIABLE_SYMBOL R_BRACE PERCENT_SIGN?; + +//collection of accents +accent_symbol: + '\\acute' | + '\\bar' | + '\\overline' | + '\\breve' | + '\\check' | + '\\widecheck' | + '\\dot' | + '\\ddot' | + '\\grave' | + '\\hat' | + '\\tilde' | + '\\widetilde' | + '\\vec' | + '\\overrightarrow' | + '\\bm' | + '\\boldsymbol' | + '\\text' | + '\\textit' | + '\\mathbb' | + '\\mathbin' | + '\\mathbf' | + '\\mathcal' | + '\\mathclap' | + '\\mathclose' | + '\\mathellipsis' | + '\\mathfrak' | + '\\mathinner' | + '\\mathit' | + '\\mathnormal' | + '\\mathop' | + '\\mathopen' | + '\\mathord' | + '\\mathpunct' | + '\\mathrel' | + '\\mathring' | + '\\mathrlap' | + '\\mathrm' | + '\\mathscr' | + '\\mathsf' | + '\\mathsterling' | + '\\mathtt'; + +math: relation | relation_list; + +transpose: '^T' | '^{T}' | '^{\\top}' | '\''; + +transform_atom: LETTER_NO_E UNDERSCORE (NUMBER | L_BRACE NUMBER R_BRACE); +transform_scale: (expr | group | ADD | SUB) transform_atom; +transform_swap: transform_atom TRANSFORM_EXCHANGE transform_atom; +transform_assignment: transform_atom transform_scale; +elementary_transform: transform_assignment | transform_scale | transform_swap; +elementary_transforms: elementary_transform (COMMA elementary_transform)*; + +matrix: + CMD_MATRIX_START + matrix_row (MATRIX_DEL_ROW matrix_row)* MATRIX_DEL_ROW? + CMD_MATRIX_END + (MATRIX_XRIGHTARROW (L_BRACKET elementary_transforms R_BRACKET)? L_BRACE elementary_transforms R_BRACE)?; + +det: + CMD_DET_START + matrix_row (MATRIX_DEL_ROW matrix_row)* MATRIX_DEL_ROW? + CMD_DET_END; + +matrix_row: + expr (MATRIX_DEL_COL expr)*; + +relation: + relation (IN | ASSIGNMENT | EQUAL | LT | LTE | GT | GTE | UNEQUAL) relation + | expr; + +relation_list: + relation_list_content + | L_BRACKET relation_list_content R_BRACKET + | L_BRACE relation_list_content R_BRACE + | L_BRACE_VISUAL relation_list_content R_BRACE_VISUAL + | L_LEFT L_BRACKET relation_list_content R_RIGHT R_BRACKET + | L_LEFT L_BRACE_VISUAL relation_list_content R_RIGHT R_BRACE_VISUAL + | ML_LEFT L_BRACKET relation_list_content MR_RIGHT R_BRACKET + | ML_LEFT L_BRACE_VISUAL relation_list_content MR_RIGHT R_BRACE_VISUAL; + +relation_list_content: + relation COMMA relation (COMMA relation)* + | relation SEMICOLON relation (SEMICOLON relation)*; + +equality: + expr (EQUAL | ASSIGNMENT) expr; + +expr: additive; + +additive: + additive (ADD | SUB) additive + | mp; + +// mult part +mp: + mp (MUL | CMD_TIMES | CMD_CDOT | DIV | CMD_DIV | COLON | CMD_MOD) mp + | unary; + +mp_nofunc: + mp_nofunc (MUL | CMD_TIMES | CMD_CDOT | DIV | CMD_DIV | COLON | CMD_MOD) mp_nofunc + | unary_nofunc; + +unary: + (ADD | SUB) unary + | postfix+; + +unary_nofunc: + (ADD | SUB) unary_nofunc + | postfix postfix_nofunc*; + +postfix: exp postfix_op*; +postfix_nofunc: exp_nofunc postfix_op*; +postfix_op: BANG | eval_at | transpose; + +eval_at: + BAR (eval_at_sup | eval_at_sub | eval_at_sup eval_at_sub); + +eval_at_sub: + UNDERSCORE L_BRACE + (expr | equality) + R_BRACE; + +eval_at_sup: + CARET L_BRACE + (expr | equality) + R_BRACE; + +exp: + exp CARET (atom | L_BRACE expr R_BRACE) subexpr? + | comp; + +exp_nofunc: + exp_nofunc CARET (atom | L_BRACE expr R_BRACE) subexpr? + | comp_nofunc; + +comp: + group + | norm_group + | abs_group + | floor_group + | ceil_group + | func + | atom + | frac + | binom + | matrix + | det; + +comp_nofunc: + group + | norm_group + | abs_group + | floor_group + | ceil_group + | atom + | frac + | binom + | matrix + | det; + +group: + L_PAREN expr R_PAREN + | L_GROUP expr R_GROUP + | L_BRACE expr R_BRACE + | L_BRACE_VISUAL expr R_BRACE_VISUAL + | L_BRACE_CMD expr R_BRACE_CMD + | L_BRACKET expr R_BRACKET + | L_BRACK expr R_BRACK + | L_LEFT L_PAREN expr R_RIGHT R_PAREN + | L_LEFT L_GROUP expr R_RIGHT R_GROUP + | L_LEFT L_BRACE expr R_RIGHT R_BRACE + | L_LEFT L_BRACE_VISUAL expr R_RIGHT R_BRACE_VISUAL + | L_LEFT L_BRACE_CMD expr R_RIGHT R_BRACE_CMD + | L_LEFT L_BRACKET expr R_RIGHT R_BRACKET + | L_LEFT L_BRACK expr R_RIGHT R_BRACK + | ML_LEFT L_PAREN expr MR_RIGHT R_PAREN + | ML_LEFT L_GROUP expr MR_RIGHT R_GROUP + | ML_LEFT L_BRACE expr MR_RIGHT R_BRACE + | ML_LEFT L_BRACE_VISUAL expr MR_RIGHT R_BRACE_VISUAL + | ML_LEFT L_BRACE_CMD expr MR_RIGHT R_BRACE_CMD + | ML_LEFT L_BRACKET expr MR_RIGHT R_BRACKET + | ML_LEFT L_BRACK expr MR_RIGHT R_BRACK; + + +norm_group: + NORM expr NORM + | L_LEFT NORM expr R_RIGHT NORM + | ML_LEFT NORM expr MR_RIGHT NORM; + + +abs_group: + BAR expr BAR + | L_VERT expr R_VERT + | VERT expr VERT + | L_LEFT BAR expr R_RIGHT BAR + | L_LEFT L_VERT expr R_RIGHT R_VERT + | L_LEFT VERT expr R_RIGHT VERT + | ML_LEFT BAR expr MR_RIGHT BAR + | ML_LEFT L_VERT expr MR_RIGHT R_VERT + | ML_LEFT VERT expr MR_RIGHT VERT; + + +floor_group: + L_FLOOR expr R_FLOOR + | LL_CORNER expr LR_CORNER + | L_LEFT L_FLOOR expr R_RIGHT R_FLOOR + | L_LEFT LL_CORNER expr R_RIGHT LR_CORNER + | ML_LEFT L_FLOOR expr MR_RIGHT R_FLOOR + | ML_LEFT LL_CORNER expr MR_RIGHT LR_CORNER; + + +ceil_group: + L_CEIL expr R_CEIL + | UL_CORNER expr UR_CORNER + | L_LEFT L_CEIL expr R_RIGHT R_CEIL + | L_LEFT UL_CORNER expr R_RIGHT UR_CORNER + | ML_LEFT L_CEIL expr MR_RIGHT R_CEIL + | ML_LEFT UL_CORNER expr MR_RIGHT UR_CORNER; + + +//indicate an accent +accent: + accent_symbol + L_BRACE base=expr R_BRACE; + +atom_expr_no_supexpr: (LETTER_NO_E | GREEK_CMD | OTHER_SYMBOL_CMD | accent) subexpr?; +atom_expr: (LETTER_NO_E | GREEK_CMD | OTHER_SYMBOL_CMD | accent) (supexpr subexpr | subexpr supexpr | subexpr | supexpr)?; +atom: atom_expr | SYMBOL | NUMBER | PERCENT_NUMBER | E_NOTATION | DIFFERENTIAL | mathit | VARIABLE; + +mathit: CMD_MATHIT L_BRACE mathit_text R_BRACE; +mathit_text: (LETTER_NO_E | E_NOTATION_E | EXP_E)+; + +frac: + CMD_FRAC L_BRACE + upper=expr + R_BRACE L_BRACE + lower=expr + R_BRACE; + +//a binomial expression +binom: + L_BRACE upper=expr CMD_CHOOSE lower=expr R_BRACE + | CMD_BINOM L_BRACE upper=expr R_BRACE L_BRACE lower=expr R_BRACE; + +func_normal_functions_single_arg: + FUNC_LOG | FUNC_LN | FUNC_EXP + | FUNC_SIN | FUNC_COS | FUNC_TAN + | FUNC_CSC | FUNC_SEC | FUNC_COT + | FUNC_ARCSIN | FUNC_ARCCOS | FUNC_ARCTAN + | FUNC_ARCCSC | FUNC_ARCSEC | FUNC_ARCCOT + | FUNC_SINH | FUNC_COSH | FUNC_TANH + | FUNC_ARSINH | FUNC_ARCOSH | FUNC_ARTANH + | FUNC_ARCSINH | FUNC_ARCCOSH | FUNC_ARCTANH + | FUNC_FLOOR | FUNC_CEIL | FUNC_DET; + +func_normal_functions_multi_arg: + FUNC_GCD | FUNC_LCM | FUNC_MAX | FUNC_MIN; + +func_operator_names_single_arg: + FUNC_ARSINH_NAME | FUNC_ARCOSH_NAME | FUNC_ARTANH_NAME + | FUNC_ARCSINH_NAME | FUNC_ARCCOSH_NAME | FUNC_ARCTANH_NAME + | FUNC_FLOOR_NAME | FUNC_CEIL_NAME | FUNC_EYE_NAME | FUNC_RANK_NAME | FUNC_TRACE_NAME + | FUNC_RREF_NAME | FUNC_NULLSPACE_NAME | FUNC_DIAGONALIZE_NAME | FUNC_NORM_NAME + | FUNC_EIGENVALS_NAME | FUNC_EIGENVECTORS_NAME | FUNC_SVD_NAME | FUNC_COLS_NAME | FUNC_ROWS_NAME; + +func_operator_names_multi_arg: + FUNC_GCD_NAME | FUNC_LCM_NAME | FUNC_ZEROS_NAME | FUNC_ORTHOGONALIZE_NAME + | FUNC_ONES_NAME | FUNC_DIAG_NAME | FUNC_HSTACK_NAME | FUNC_VSTACK_NAME; + +func_normal_single_arg: + (func_normal_functions_single_arg) + | + (CMD_OPERATORNAME L_BRACE func_operator_name=func_operator_names_single_arg R_BRACE); + +func_normal_multi_arg: + (func_normal_functions_multi_arg) + | + (CMD_OPERATORNAME L_BRACE func_operator_name=func_operator_names_multi_arg R_BRACE); + +func: + func_normal_single_arg + (subexpr? supexpr? | supexpr? subexpr?) + (L_LEFT? L_PAREN func_single_arg R_RIGHT? R_PAREN | ML_LEFT? L_PAREN func_single_arg MR_RIGHT? R_PAREN | func_single_arg_noparens) + + | func_normal_multi_arg + (subexpr? supexpr? | supexpr? subexpr?) + (L_LEFT? L_PAREN func_multi_arg R_RIGHT? R_PAREN | ML_LEFT? L_PAREN func_multi_arg MR_RIGHT? R_PAREN | func_multi_arg_noparens) + + | atom_expr_no_supexpr supexpr? + L_LEFT? (L_PAREN | L_BRACKET) func_common_args (R_PAREN | R_BRACKET) R_RIGHT? + | atom_expr_no_supexpr supexpr? + L_BRACE L_LEFT? (L_PAREN | L_BRACKET) func_common_args (R_PAREN | R_BRACKET) R_RIGHT? R_BRACE + + | FUNC_INT + (subexpr supexpr | supexpr subexpr | (UNDERSCORE L_BRACE R_BRACE) (CARET L_BRACE R_BRACE) | (CARET L_BRACE R_BRACE) (UNDERSCORE L_BRACE R_BRACE) )? + (additive? DIFFERENTIAL | frac | additive) + + | FUNC_SQRT + (L_BRACKET root=expr R_BRACKET)? + L_BRACE base=expr R_BRACE + + | (FUNC_SUM | FUNC_PROD) + (subeq supexpr | supexpr subeq) + mp + | FUNC_LIM limit_sub mp + | EXP_E supexpr?; //Exponential function e^x + +args: (expr ',' args) | expr; + +func_common_args: atom | (expr ',') | (expr ',' args); + +limit_sub: + UNDERSCORE L_BRACE + (LETTER_NO_E | GREEK_CMD | OTHER_SYMBOL_CMD) + LIM_APPROACH_SYM + expr (CARET L_BRACE (ADD | SUB) R_BRACE)? + R_BRACE; + +func_single_arg: expr; +func_single_arg_noparens: mp_nofunc; + +func_multi_arg: expr | (expr ',' func_multi_arg); +func_multi_arg_noparens: mp_nofunc; + +subexpr: UNDERSCORE (atom | L_BRACE (expr | args) R_BRACE); +supexpr: CARET (atom | L_BRACE expr R_BRACE); + +subeq: UNDERSCORE L_BRACE equality R_BRACE; +supeq: UNDERSCORE L_BRACE equality R_BRACE; diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/README.md b/Qwen2.5-Eval/evaluation/latex2sympy/README.md new file mode 100755 index 0000000..2e8b92c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/README.md @@ -0,0 +1,196 @@ +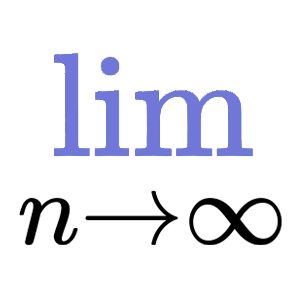 + +# [latex2sympy2](https://github.com/OrangeX4/latex2sympy) + +## About + +`latex2sympy2` parses **LaTeX math expressions** and converts it into the equivalent **SymPy form**. The latex2sympy2 is adapted from [augustt198/latex2sympy](https://github.com/augustt198/latex2sympy) and [purdue-tlt / latex2sympy](https://github.com/purdue-tlt/latex2sympy). + +This project is a part of a VS Code extension called [Latex Sympy Calculator](https://marketplace.visualstudio.com/items?itemName=OrangeX4.latex-sympy-calculator). It is designed for providing people writing in latex or markdown a ability to calculate something when writing math expression. + +[ANTLR](http://www.antlr.org/) is used to generate the parser. + +## Features + +* **Arithmetic:** Add (+), Sub (-), Dot Mul (·), Cross Mul (×), Frac (/), Power (^), Abs (|x|), Sqrt (√), etc... +* **Alphabet:** a - z, A - Z, α - ω, Subscript (x_1), Accent Bar(ā), etc... +* **Common Functions:** gcd, lcm, floor, ceil, max, min, log, ln, exp, sin, cos, tan, csc, sec, cot, arcsin, sinh, arsinh, etc... +* **Funcion Symbol:** f(x), f(x-1,), g(x,y), etc... +* **Calculous:** Limit ($lim_{n\to\infty}$), Derivation ($\frac{d}{dx}(x^2+x)$), Integration ($\int xdx$), etc... +* **Linear Algebra:** Matrix, Determinant, Transpose, Inverse, Elementary Transformation, etc... +* **Other:** Binomial... + +**NOTICE:** It will do some irreversible calculations when converting determinants, transposed matrixes and elementary transformations... + +## Installation + +``` +pip install latex2sympy2 +``` + +**Requirements:** `sympy` and `antlr4-python3-runtime` packages. + +## Usage + +### Basic + +In Python: + +```python +from latex2sympy2 import latex2sympy, latex2latex + +tex = r"\frac{d}{dx}(x^{2}+x)" +# Or you can use '\mathrm{d}' to replace 'd' +latex2sympy(tex) +# => "Derivative(x**2 + x, x)" +latex2latex(tex) +# => "2 x + 1" +``` + +### Examples + +|LaTeX|Converted SymPy|Calculated Latex| +|-----|-----|---------------| +|`x^{3}` $x^{3}$| `x**3`|`x^{3}` $x^{3}$| +|`\frac{d}{dx} tx` $\frac{d}{dx}tx$|`Derivative(x*t, x)`|`t` $t$| +|`\sum_{i = 1}^{n} i` $\sum_{i = 1}^{n} i$|`Sum(i, (i, 1, n))`|`\frac{n \left(n + 1\right)}{2}` $\frac{n \left(n + 1\right)}{2}$| +|`\int_{a}^{b} \frac{dt}{t}`|`Integral(1/t, (t, a, b))`|`-\log{(a)} + \log{(b)}` $-\log{(a)} + \log{(b)}$| +|`(2x^3 - x + z)|_{x=3}` $(2x^3 - x + z)\|_{x=3}$|`z + 51`| `z + 51` $z + 51$ | + +If you want to read the math formula, you can click [GitNotes](https://notes.orangex4.cool/?git=github&github=OrangeX4/latex2sympy). + +### Solve Equation + +``` latex +# Before +x + y = 1 + +# After +[ y = 1 - x, \ x = 1 - y] +``` + +### Eval At + +``` latex +# Before +(x+2)|_{x=y+1} + +# After +y + 3 +``` + +### Matrix + +#### Identity matrix + +``` +tex = r"\bm{I}_3" +latex2sympy(tex) +# => "Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])" +``` + +#### Determinant + +``` python +from latex2sympy2 import latex2sympy + +tex = r"\begin{vmatrix} x & 0 & 0 \\ 0 & x & 0 \\ 0 & 0 & x \end{vmatrix}" +latex2sympy(tex) +# => "x^{3}" +``` + +#### Transpose + +``` python +from latex2sympy2 import latex2sympy + +tex = r"\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}^T" +# Or you can use "\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}'" +latex2sympy(tex) +# => "Matrix([[1, 4, 7], [2, 5, 8], [3, 6, 9]])" +``` + +#### Elementary Transformation + +``` python +from latex2sympy2 import latex2sympy + +matrix = r''' + \begin{pmatrix} + 1 & 2 & 3 \\ + 4 & 5 & 6 \\ + 7 & 8 & 9 \\ + \end{pmatrix} +''' + +# Scale the row with grammar "\xrightarrow{kr_n}" +tex = matrix + r'\xrightarrow{3r_1}' +latex2sympy(tex) +# => "Matrix([[3, 6, 9], [4, 5, 6], [7, 8, 9]])" + +# Swap the cols with grammar "\xrightarrow{c_1<=>c_2}" +# Of course, you can use "\leftrightarrow" to replace "<=>" +tex = matrix + r'\xrightarrow{c_1<=>c_2}' +latex2sympy(tex) +# => "Matrix([[2, 1, 3], [5, 4, 6], [8, 7, 9]])" + +# Scale the second row and add it to the first row +# with grammar "\xrightarrow{r_1+kr_2}" +tex = matrix + r'\xrightarrow{r_1+kr_2}' +latex2sympy(tex) +# => "Matrix([[4*k + 1, 5*k + 2, 6*k + 3], [4, 5, 6], [7, 8, 9]])" + +# You can compose the transform with comma "," +# and grammar "\xrightarrow[4r_3]{2r_1, 3r_2}" +# Remember the priority of "{}" is higher than "[]" +tex = matrix + r'\xrightarrow[4r_3]{2r_1, 3r_2}' +latex2sympy(tex) +# => "Matrix([[2, 4, 6], [12, 15, 18], [28, 32, 36]])" +``` + +### Variances + +``` python +from latex2sympy2 import latex2sympy, variances, var, set_variances + +# Assign x a value of 1 +latex2sympy(r"x = 1") + +# Assign x a matrix symbol with dimension of n x m +latex2sympy(r"x \in \mathbb{R}^{n \times m}") + +# Calculate x + y +latex2sympy(r"x + y") +# => "y + 1" + +# Get all variances +print(variances) +# => "{x: 1}" + +# Get variance of "x" +print(var["x"]) +# => "1" + +# Reset all variances +set_variances({}) +latex2sympy(r"x + y") +# => "x + y" +``` + +### Complex Number Support + +``` python +from latex2sympy2 import set_real + +set_real(False) +``` + + +## Contributing + +If you want to add a new grammar, you can fork the code from [OrangeX4/latex2sympy](https://github.com/OrangeX4/latex2sympy). + +* To modify parser grammar, view the existing structure in `PS.g4`. +* To modify the action associated with each grammar, look into `latex2sympy.py`. + +Contributors are welcome! Feel free to open a pull request or an issue. diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/__init__.py b/Qwen2.5-Eval/evaluation/latex2sympy/__init__.py new file mode 100755 index 0000000..28a11cf --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/__init__.py @@ -0,0 +1 @@ +import latex2sympy
\ No newline at end of file diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/antlr-4.11.1-complete.jar b/Qwen2.5-Eval/evaluation/latex2sympy/antlr-4.11.1-complete.jar Binary files differnew file mode 100755 index 0000000..bb96df9 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/antlr-4.11.1-complete.jar diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/asciimath_printer.py b/Qwen2.5-Eval/evaluation/latex2sympy/asciimath_printer.py new file mode 100755 index 0000000..dd1b676 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/asciimath_printer.py @@ -0,0 +1,50 @@ +from sympy.printing.str import StrPrinter +from sympy.core import S + +class AsciiMathPrinter(StrPrinter): + + def _print_Limit(self, expr): + e, z = expr.args + + return "lim_(%s -> %s) %s" % (self._print(z), self._print(z), self._print(e)) + + def _print_Integral(self, expr): + e, lims = expr.args + if len(lims) > 1: + return "int_(%s)^(%s) %s d%s" % (self._print(lims[1]), self._print(lims[2]), self._print(e), self._print(lims[0])) + else: + return "int %s d%s" % (self._print(e), self._print(lims)) + + def _print_Sum(self, expr): + e, lims = expr.args + return "sum_(%s = %s)^(%s) %s" % (self._print(lims[0]), self._print(lims[1]), self._print(lims[2]), self._print(e)) + + def _print_Product(self, expr): + e, lims = expr.args + return "prod_(%s = %s)^(%s) %s" % (self._print(lims[0]), self._print(lims[1]), self._print(lims[2]), self._print(e)) + + def _print_factorial(self, expr): + return "%s!" % self._print(expr.args[0]) + + def _print_Derivative(self, expr): + e = expr.args[0] + wrt = expr.args[1] + return "d/d%s %s" % (self._print(wrt), self._print(e)) + + def _print_Abs(self, expr): + return "|%s|" % self._print(expr.args[0]) + + def _print_Equality(self, expr): + return "%s = %s" % (self._print(expr.args[0]), self._print(expr.args[1])) + + def _print_Pow(self, expr): + b = self._print(expr.base) + if expr.exp is S.Half: + return "sqrt(%s)" % b + + if -expr.exp is S.Half: + return "1/sqrt(%s)" % b + if expr.exp is -S.One: + return "1/%s" % b + + return "%s^(%s)" % (b, self._print(expr.exp)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/description.txt b/Qwen2.5-Eval/evaluation/latex2sympy/description.txt new file mode 100755 index 0000000..0064c1f --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/description.txt @@ -0,0 +1,152 @@ +latex2sympy2: https://github.com/OrangeX4/latex2sympy + +About + +`latex2sympy2` parses **LaTeX math expressions** and converts it into the equivalent **SymPy form**. The latex2sympy2 is adapted from [augustt198/latex2sympy](https://github.com/augustt198/latex2sympy) and [purdue-tlt / latex2sympy](https://github.com/purdue-tlt/latex2sympy). + +[ANTLR](http://www.antlr.org/) is used to generate the parser. + +Features + +* **Arithmetic:** Add (+), Sub (-), Dot Mul (·), Cross Mul (×), Frac (/), Power (^), Abs (|x|), Sqrt (√), etc... +* **Alphabet:** a - z, A - Z, α - ω, Subscript (x_1), Accent Bar(ā), etc... +* **Common Functions:** gcd, lcm, floor, ceil, max, min, log, ln, exp, sin, cos, tan, csc, sec, cot, arcsin, sinh, arsinh, etc... +* **Calculous:** Limit ($lim_{n\to\infty}$), Derivation ($\frac{d}{dx}(x^2+x)$), Integration ($\int xdx$), etc... +* **Linear Algebra:** Matrix, Determinant, Transpose, Inverse, Elementary Transformation, etc... +* **Other:** Binomial... + +**NOTICE:** It will do some irreversible calculations when converting determinants, transposed matrixes and elementary transformations... + +Installation + +``` +pip install latex2sympy2 +``` + +**Requirements:** `sympy` and `antlr4-python3-runtime` packages. + +Usage + + Basic + +In Python: + +```python +from latex2sympy2 import latex2sympy, latex2latex + +tex = r"\frac{d}{dx}(x^{2}+x)" +# Or you can use '\mathrm{d}' to replace 'd' +latex2sympy(tex) +# => "Derivative(x**2 + x, x)" +latex2latex(tex) +# => "2 x + 1" +``` + + Examples + +|LaTeX|Converted SymPy|Calculated Latex| +|-----|-----|---------------| +|`x^{3}` $x^{3}$| `x**3`|`x^{3}` $x^{3}$| +|`\frac{d}{dx} tx` $\frac{d}{dx}tx$|`Derivative(x*t, x)`|`t` $t$| +|`\sum_{i = 1}^{n} i` $\sum_{i = 1}^{n} i$|`Sum(i, (i, 1, n))`|`\frac{n \left(n + 1\right)}{2}` $\frac{n \left(n + 1\right)}{2}$| +|`\int_{a}^{b} \frac{dt}{t}`|`Integral(1/t, (t, a, b))`|`-\log{(a)} + \log{(b)}` $-\log{(a)} + \log{(b)}$| +|`(2x^3 - x + z)|_{x=3}` $(2x^3 - x + z)\|_{x=3}$|`z + 51`| `z + 51` $z + 51$ | + +If you want to read the math formula, you can click [GitNotes](https://notes.orangex4.cool/?git=github&github=OrangeX4/latex2sympy). + + Matrix + +Determinant + +``` python +from latex2sympy2 import latex2sympy + +tex = r"\begin{vmatrix} x & 0 & 0 \\ 0 & x & 0 \\ 0 & 0 & x \end{vmatrix}" +latex2sympy(tex) +# => "x^{3}" +``` + +Transpose + +``` python +from latex2sympy2 import latex2sympy + +tex = r"\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}^T" +# Or you can use "\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}'" +latex2sympy(tex) +# => "Matrix([[1, 4, 7], [2, 5, 8], [3, 6, 9]])" +``` + +Elementary Transformation + +``` python +from latex2sympy2 import latex2sympy + +matrix = r''' + \begin{pmatrix} + 1 & 2 & 3 \\ + 4 & 5 & 6 \\ + 7 & 8 & 9 \\ + \end{pmatrix} +''' + +# Scale the row with grammar "\xrightarrow{kr_n}" +tex = matrix + r'\xrightarrow{3r_1}' +latex2sympy(tex) +# => "Matrix([[3, 6, 9], [4, 5, 6], [7, 8, 9]])" + +# Swap the cols with grammar "\xrightarrow{c_1<=>c_2}" +# Of course, you can use "\leftrightarrow" to replace "<=>" +tex = matrix + r'\xrightarrow{c_1<=>c_2}' +latex2sympy(tex) +# => "Matrix([[2, 1, 3], [5, 4, 6], [8, 7, 9]])" + +# Scale the second row and add it to the first row +# with grammar "\xrightarrow{r_1+kr_2}" +tex = matrix + r'\xrightarrow{r_1+kr_2}' +latex2sympy(tex) +# => "Matrix([[4*k + 1, 5*k + 2, 6*k + 3], [4, 5, 6], [7, 8, 9]])" + +# You can compose the transform with comma "," +# and grammar "\xrightarrow[4r_3]{2r_1, 3r_2}" +# Remember the priority of "{}" is higher than "[]" +tex = matrix + r'\xrightarrow[4r_3]{2r_1, 3r_2}' +latex2sympy(tex) +# => "Matrix([[2, 4, 6], [12, 15, 18], [28, 32, 36]])" +``` + + Variances + +``` python +from latex2sympy2 import latex2sympy, variances, var, set_variances + +# Assign x a value of 1 +latex2sympy(r"x = 1") + +# Calculate x + y +latex2sympy(r"x + y") +# => "y + 1" + +# Get all variances +print(variances) +# => "{x: 1}" + +# Get variance of "x" +print(var["x"]) +# => "1" + +# Reset all variances +set_variances({}) +latex2sympy(r"x + y") +# => "x + y" +``` + + +Contributing + +If you want to add a new grammar, you can fork the code from [OrangeX4/latex2sympy](https://github.com/OrangeX4/latex2sympy). + +* To modify parser grammar, view the existing structure in `PS.g4`. +* To modify the action associated with each grammar, look into `latex2sympy.py`. + +Contributors are welcome! Feel free to open a pull request or an issue. diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/dev-requirements.in b/Qwen2.5-Eval/evaluation/latex2sympy/dev-requirements.in new file mode 100755 index 0000000..80a4877 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/dev-requirements.in @@ -0,0 +1,8 @@ +-r requirements.txt +# Development +pip-tools +pytest +pytest-cov +pycodestyle +autopep8 +-e . diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/dev-requirements.txt b/Qwen2.5-Eval/evaluation/latex2sympy/dev-requirements.txt new file mode 100755 index 0000000..4e2c43c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/dev-requirements.txt @@ -0,0 +1,60 @@ +# +# This file is autogenerated by pip-compile with Python 3.10 +# by the following command: +# +# pip-compile dev-requirements.in +# + # via -r dev-requirements.in +antlr4-python3-runtime==4.11.1 + # via + # -r requirements.txt + # latex2sympy2 +atomicwrites==1.3.0 + # via pytest +attrs==19.3.0 + # via pytest +autopep8==1.4.4 + # via -r dev-requirements.in +click==7.0 + # via pip-tools +coverage==4.5.4 + # via pytest-cov +more-itertools==7.2.0 + # via pytest +mpmath==1.3.0 + # via + # -r requirements.txt + # sympy +packaging==19.2 + # via pytest +pip-tools==4.2.0 + # via -r dev-requirements.in +pluggy==0.13.0 + # via pytest +py==1.8.0 + # via pytest +pycodestyle==2.5.0 + # via + # -r dev-requirements.in + # autopep8 +pyparsing==2.4.4 + # via packaging +pytest==5.2.2 + # via + # -r dev-requirements.in + # pytest-cov +pytest-cov==2.8.1 + # via -r dev-requirements.in +six==1.13.0 + # via + # packaging + # pip-tools +sympy==1.12 + # via + # -r requirements.txt + # latex2sympy2 +wcwidth==0.1.7 + # via pytest + +# THIS MUST BE MAINTAINED AS-IS +-e .
\ No newline at end of file diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/PS.interp b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PS.interp new file mode 100755 index 0000000..82d050c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PS.interp @@ -0,0 +1,462 @@ +token literal names: +null +'\\acute' +'\\bar' +'\\overline' +'\\breve' +'\\check' +'\\widecheck' +'\\dot' +'\\ddot' +'\\grave' +'\\hat' +'\\tilde' +'\\widetilde' +'\\vec' +'\\overrightarrow' +'\\bm' +'\\boldsymbol' +'\\text' +'\\textit' +'\\mathbb' +'\\mathbin' +'\\mathbf' +'\\mathcal' +'\\mathclap' +'\\mathclose' +'\\mathellipsis' +'\\mathfrak' +'\\mathinner' +'\\mathnormal' +'\\mathop' +'\\mathopen' +'\\mathord' +'\\mathpunct' +'\\mathrel' +'\\mathring' +'\\mathrlap' +'\\mathrm' +'\\mathscr' +'\\mathsf' +'\\mathsterling' +'\\mathtt' +'^T' +'^{T}' +'^{\\top}' +'\'' +null +'\\$' +'+' +'-' +'*' +null +'(' +')' +'\\lgroup' +'\\rgroup' +'{' +'}' +'\\{' +'\\}' +'\\lbrace' +'\\rbrace' +'[' +']' +'\\lbrack' +'\\rbrack' +'|' +'\\lvert' +'\\rvert' +'\\vert' +'\\|' +'\\lfloor' +'\\rfloor' +'\\llcorner' +'\\lrcorner' +'\\lceil' +'\\rceil' +'\\ulcorner' +'\\urcorner' +'\\left' +'\\right' +'\\mleft' +'\\mright' +'\\lim' +null +'\\int' +'\\sum' +'\\prod' +'\\log' +'\\ln' +'\\exp' +'\\sin' +'\\cos' +'\\tan' +'\\csc' +'\\sec' +'\\cot' +'\\arcsin' +'\\arccos' +'\\arctan' +'\\arccsc' +'\\arcsec' +'\\arccot' +'\\sinh' +'\\cosh' +'\\tanh' +'\\arsinh' +'\\arcosh' +'\\artanh' +'\\arcsinh' +'\\arccosh' +'\\arctanh' +'arsinh' +'arcsinh' +'arcosh' +'arccosh' +'artanh' +'arctanh' +'gcd' +'lcm' +'floor' +'ceil' +'\\sqrt' +'\\gcd' +'\\lcm' +'\\floor' +'\\ceil' +'\\max' +'\\min' +'\\det' +'eye' +'zeros' +'ones' +'cols' +'rows' +'diag' +'norm' +'rank' +null +'rref' +'hstack' +'vstack' +null +'nullspace' +null +null +null +null +'\\times' +'\\cdot' +'\\div' +'\\frac' +null +'\\choose' +'\\mod' +'\\mathit' +'\\operatorname' +'matrix' +'pmatrix' +'bmatrix' +'vmatrix' +null +null +null +null +null +'&' +'\\\\' +'_' +'^' +':' +';' +',' +'.' +null +null +'E' +null +null +null +null +null +'\\in' +'=' +null +'<' +null +'>' +null +null +'!' +null +null +null +null +null + +token symbolic names: +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +WS +DOLLAR_SIGN +ADD +SUB +MUL +DIV +L_PAREN +R_PAREN +L_GROUP +R_GROUP +L_BRACE +R_BRACE +L_BRACE_VISUAL +R_BRACE_VISUAL +L_BRACE_CMD +R_BRACE_CMD +L_BRACKET +R_BRACKET +L_BRACK +R_BRACK +BAR +L_VERT +R_VERT +VERT +NORM +L_FLOOR +R_FLOOR +LL_CORNER +LR_CORNER +L_CEIL +R_CEIL +UL_CORNER +UR_CORNER +L_LEFT +R_RIGHT +ML_LEFT +MR_RIGHT +FUNC_LIM +LIM_APPROACH_SYM +FUNC_INT +FUNC_SUM +FUNC_PROD +FUNC_LOG +FUNC_LN +FUNC_EXP +FUNC_SIN +FUNC_COS +FUNC_TAN +FUNC_CSC +FUNC_SEC +FUNC_COT +FUNC_ARCSIN +FUNC_ARCCOS +FUNC_ARCTAN +FUNC_ARCCSC +FUNC_ARCSEC +FUNC_ARCCOT +FUNC_SINH +FUNC_COSH +FUNC_TANH +FUNC_ARSINH +FUNC_ARCOSH +FUNC_ARTANH +FUNC_ARCSINH +FUNC_ARCCOSH +FUNC_ARCTANH +FUNC_ARSINH_NAME +FUNC_ARCSINH_NAME +FUNC_ARCOSH_NAME +FUNC_ARCCOSH_NAME +FUNC_ARTANH_NAME +FUNC_ARCTANH_NAME +FUNC_GCD_NAME +FUNC_LCM_NAME +FUNC_FLOOR_NAME +FUNC_CEIL_NAME +FUNC_SQRT +FUNC_GCD +FUNC_LCM +FUNC_FLOOR +FUNC_CEIL +FUNC_MAX +FUNC_MIN +FUNC_DET +FUNC_EYE_NAME +FUNC_ZEROS_NAME +FUNC_ONES_NAME +FUNC_COLS_NAME +FUNC_ROWS_NAME +FUNC_DIAG_NAME +FUNC_NORM_NAME +FUNC_RANK_NAME +FUNC_TRACE_NAME +FUNC_RREF_NAME +FUNC_HSTACK_NAME +FUNC_VSTACK_NAME +FUNC_ORTHOGONALIZE_NAME +FUNC_NULLSPACE_NAME +FUNC_DIAGONALIZE_NAME +FUNC_EIGENVALS_NAME +FUNC_EIGENVECTORS_NAME +FUNC_SVD_NAME +CMD_TIMES +CMD_CDOT +CMD_DIV +CMD_FRAC +CMD_BINOM +CMD_CHOOSE +CMD_MOD +CMD_MATHIT +CMD_OPERATORNAME +MATRIX_TYPE_MATRIX +MATRIX_TYPE_PMATRIX +MATRIX_TYPE_BMATRIX +MATRIX_TYPE_DET +MATRIX_TYPES +CMD_MATRIX_START +CMD_MATRIX_END +CMD_DET_START +CMD_DET_END +MATRIX_DEL_COL +MATRIX_DEL_ROW +UNDERSCORE +CARET +COLON +SEMICOLON +COMMA +PERIOD +DIFFERENTIAL +EXP_E +E_NOTATION_E +LETTER_NO_E +MATRIX_XRIGHTARROW +TRANSFORM_EXCHANGE +NUMBER +E_NOTATION +IN +ASSIGNMENT +EQUAL +LT +LTE +GT +GTE +UNEQUAL +BANG +PERCENT_NUMBER +GREEK_CMD +OTHER_SYMBOL_CMD +SYMBOL +VARIABLE + +rule names: +accent_symbol +math +transpose +transform_atom +transform_scale +transform_swap +transform_assignment +elementary_transform +elementary_transforms +matrix +det +matrix_row +relation +relation_list +relation_list_content +equality +expr +additive +mp +mp_nofunc +unary +unary_nofunc +postfix +postfix_nofunc +postfix_op +eval_at +eval_at_sub +eval_at_sup +exp +exp_nofunc +comp +comp_nofunc +group +norm_group +abs_group +floor_group +ceil_group +accent +atom_expr_no_supexpr +atom_expr +atom +mathit +mathit_text +frac +binom +func_normal_functions_single_arg +func_normal_functions_multi_arg +func_operator_names_single_arg +func_operator_names_multi_arg +func_normal_single_arg +func_normal_multi_arg +func +args +func_common_args +limit_sub +func_single_arg +func_single_arg_noparens +func_multi_arg +func_multi_arg_noparens +subexpr +supexpr +subeq +supeq + + +atn: +[4, 1, 194, 1046, 2, 0, 7, 0, 2, 1, 7, 1, 2, 2, 7, 2, 2, 3, 7, 3, 2, 4, 7, 4, 2, 5, 7, 5, 2, 6, 7, 6, 2, 7, 7, 7, 2, 8, 7, 8, 2, 9, 7, 9, 2, 10, 7, 10, 2, 11, 7, 11, 2, 12, 7, 12, 2, 13, 7, 13, 2, 14, 7, 14, 2, 15, 7, 15, 2, 16, 7, 16, 2, 17, 7, 17, 2, 18, 7, 18, 2, 19, 7, 19, 2, 20, 7, 20, 2, 21, 7, 21, 2, 22, 7, 22, 2, 23, 7, 23, 2, 24, 7, 24, 2, 25, 7, 25, 2, 26, 7, 26, 2, 27, 7, 27, 2, 28, 7, 28, 2, 29, 7, 29, 2, 30, 7, 30, 2, 31, 7, 31, 2, 32, 7, 32, 2, 33, 7, 33, 2, 34, 7, 34, 2, 35, 7, 35, 2, 36, 7, 36, 2, 37, 7, 37, 2, 38, 7, 38, 2, 39, 7, 39, 2, 40, 7, 40, 2, 41, 7, 41, 2, 42, 7, 42, 2, 43, 7, 43, 2, 44, 7, 44, 2, 45, 7, 45, 2, 46, 7, 46, 2, 47, 7, 47, 2, 48, 7, 48, 2, 49, 7, 49, 2, 50, 7, 50, 2, 51, 7, 51, 2, 52, 7, 52, 2, 53, 7, 53, 2, 54, 7, 54, 2, 55, 7, 55, 2, 56, 7, 56, 2, 57, 7, 57, 2, 58, 7, 58, 2, 59, 7, 59, 2, 60, 7, 60, 2, 61, 7, 61, 2, 62, 7, 62, 1, 0, 1, 0, 1, 1, 1, 1, 3, 1, 131, 8, 1, 1, 2, 1, 2, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 3, 3, 141, 8, 3, 1, 4, 1, 4, 1, 4, 1, 4, 3, 4, 147, 8, 4, 1, 4, 1, 4, 1, 5, 1, 5, 1, 5, 1, 5, 1, 6, 1, 6, 1, 6, 1, 7, 1, 7, 1, 7, 3, 7, 161, 8, 7, 1, 8, 1, 8, 1, 8, 5, 8, 166, 8, 8, 10, 8, 12, 8, 169, 9, 8, 1, 9, 1, 9, 1, 9, 1, 9, 5, 9, 175, 8, 9, 10, 9, 12, 9, 178, 9, 9, 1, 9, 3, 9, 181, 8, 9, 1, 9, 1, 9, 1, 9, 1, 9, 1, 9, 1, 9, 3, 9, 189, 8, 9, 1, 9, 1, 9, 1, 9, 1, 9, 3, 9, 195, 8, 9, 1, 10, 1, 10, 1, 10, 1, 10, 5, 10, 201, 8, 10, 10, 10, 12, 10, 204, 9, 10, 1, 10, 3, 10, 207, 8, 10, 1, 10, 1, 10, 1, 11, 1, 11, 1, 11, 5, 11, 214, 8, 11, 10, 11, 12, 11, 217, 9, 11, 1, 12, 1, 12, 1, 12, 1, 12, 1, 12, 1, 12, 5, 12, 225, 8, 12, 10, 12, 12, 12, 228, 9, 12, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 3, 13, 267, 8, 13, 1, 14, 1, 14, 1, 14, 1, 14, 1, 14, 5, 14, 274, 8, 14, 10, 14, 12, 14, 277, 9, 14, 1, 14, 1, 14, 1, 14, 1, 14, 1, 14, 5, 14, 284, 8, 14, 10, 14, 12, 14, 287, 9, 14, 3, 14, 289, 8, 14, 1, 15, 1, 15, 1, 15, 1, 15, 1, 16, 1, 16, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 5, 17, 303, 8, 17, 10, 17, 12, 17, 306, 9, 17, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 5, 18, 314, 8, 18, 10, 18, 12, 18, 317, 9, 18, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 5, 19, 325, 8, 19, 10, 19, 12, 19, 328, 9, 19, 1, 20, 1, 20, 1, 20, 4, 20, 333, 8, 20, 11, 20, 12, 20, 334, 3, 20, 337, 8, 20, 1, 21, 1, 21, 1, 21, 1, 21, 5, 21, 343, 8, 21, 10, 21, 12, 21, 346, 9, 21, 3, 21, 348, 8, 21, 1, 22, 1, 22, 5, 22, 352, 8, 22, 10, 22, 12, 22, 355, 9, 22, 1, 23, 1, 23, 5, 23, 359, 8, 23, 10, 23, 12, 23, 362, 9, 23, 1, 24, 1, 24, 1, 24, 3, 24, 367, 8, 24, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 3, 25, 375, 8, 25, 1, 26, 1, 26, 1, 26, 1, 26, 3, 26, 381, 8, 26, 1, 26, 1, 26, 1, 27, 1, 27, 1, 27, 1, 27, 3, 27, 389, 8, 27, 1, 27, 1, 27, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 3, 28, 403, 8, 28, 1, 28, 3, 28, 406, 8, 28, 5, 28, 408, 8, 28, 10, 28, 12, 28, 411, 9, 28, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 3, 29, 423, 8, 29, 1, 29, 3, 29, 426, 8, 29, 5, 29, 428, 8, 29, 10, 29, 12, 29, 431, 9, 29, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 3, 30, 444, 8, 30, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 3, 31, 456, 8, 31, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 3, 32, 570, 8, 32, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 3, 33, 588, 8, 33, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 3, 34, 638, 8, 34, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 3, 35, 672, 8, 35, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 3, 36, 706, 8, 36, 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, 38, 1, 38, 1, 38, 1, 38, 3, 38, 717, 8, 38, 1, 38, 3, 38, 720, 8, 38, 1, 39, 1, 39, 1, 39, 1, 39, 3, 39, 726, 8, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 3, 39, 736, 8, 39, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 3, 40, 746, 8, 40, 1, 41, 1, 41, 1, 41, 1, 41, 1, 41, 1, 42, 4, 42, 754, 8, 42, 11, 42, 12, 42, 755, 1, 43, 1, 43, 1, 43, 1, 43, 1, 43, 1, 43, 1, 43, 1, 43, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 3, 44, 780, 8, 44, 1, 45, 1, 45, 1, 46, 1, 46, 1, 47, 1, 47, 1, 48, 1, 48, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 3, 49, 796, 8, 49, 1, 50, 1, 50, 1, 50, 1, 50, 1, 50, 1, 50, 3, 50, 804, 8, 50, 1, 51, 1, 51, 3, 51, 808, 8, 51, 1, 51, 3, 51, 811, 8, 51, 1, 51, 3, 51, 814, 8, 51, 1, 51, 3, 51, 817, 8, 51, 3, 51, 819, 8, 51, 1, 51, 3, 51, 822, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 827, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 832, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 837, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 842, 8, 51, 1, 51, 1, 51, 3, 51, 846, 8, 51, 1, 51, 3, 51, 849, 8, 51, 1, 51, 3, 51, 852, 8, 51, 1, 51, 3, 51, 855, 8, 51, 3, 51, 857, 8, 51, 1, 51, 3, 51, 860, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 865, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 870, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 875, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 880, 8, 51, 1, 51, 1, 51, 3, 51, 884, 8, 51, 1, 51, 3, 51, 887, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 893, 8, 51, 1, 51, 1, 51, 3, 51, 897, 8, 51, 1, 51, 1, 51, 3, 51, 901, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 907, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 932, 8, 51, 1, 51, 3, 51, 935, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 940, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 947, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 960, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 970, 8, 51, 3, 51, 972, 8, 51, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 3, 52, 979, 8, 52, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 3, 53, 989, 8, 53, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 3, 54, 1000, 8, 54, 1, 54, 1, 54, 1, 55, 1, 55, 1, 56, 1, 56, 1, 57, 1, 57, 1, 57, 1, 57, 1, 57, 3, 57, 1013, 8, 57, 1, 58, 1, 58, 1, 59, 1, 59, 1, 59, 1, 59, 1, 59, 3, 59, 1022, 8, 59, 1, 59, 1, 59, 3, 59, 1026, 8, 59, 1, 60, 1, 60, 1, 60, 1, 60, 1, 60, 1, 60, 3, 60, 1034, 8, 60, 1, 61, 1, 61, 1, 61, 1, 61, 1, 61, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 0, 6, 24, 34, 36, 38, 56, 58, 63, 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, 114, 116, 118, 120, 122, 124, 0, 15, 2, 0, 1, 40, 154, 154, 1, 0, 41, 44, 1, 0, 181, 188, 1, 0, 182, 183, 1, 0, 47, 48, 4, 0, 49, 50, 147, 149, 153, 153, 169, 169, 1, 0, 174, 176, 3, 0, 87, 110, 124, 125, 128, 128, 2, 0, 122, 123, 126, 127, 6, 0, 111, 116, 119, 120, 129, 129, 132, 133, 135, 138, 142, 146, 4, 0, 117, 118, 130, 131, 134, 134, 139, 141, 2, 0, 51, 51, 61, 61, 2, 0, 52, 52, 62, 62, 1, 0, 85, 86, 2, 0, 176, 176, 191, 192, 1164, 0, 126, 1, 0, 0, 0, 2, 130, 1, 0, 0, 0, 4, 132, 1, 0, 0, 0, 6, 134, 1, 0, 0, 0, 8, 146, 1, 0, 0, 0, 10, 150, 1, 0, 0, 0, 12, 154, 1, 0, 0, 0, 14, 160, 1, 0, 0, 0, 16, 162, 1, 0, 0, 0, 18, 170, 1, 0, 0, 0, 20, 196, 1, 0, 0, 0, 22, 210, 1, 0, 0, 0, 24, 218, 1, 0, 0, 0, 26, 266, 1, 0, 0, 0, 28, 288, 1, 0, 0, 0, 30, 290, 1, 0, 0, 0, 32, 294, 1, 0, 0, 0, 34, 296, 1, 0, 0, 0, 36, 307, 1, 0, 0, 0, 38, 318, 1, 0, 0, 0, 40, 336, 1, 0, 0, 0, 42, 347, 1, 0, 0, 0, 44, 349, 1, 0, 0, 0, 46, 356, 1, 0, 0, 0, 48, 366, 1, 0, 0, 0, 50, 368, 1, 0, 0, 0, 52, 376, 1, 0, 0, 0, 54, 384, 1, 0, 0, 0, 56, 392, 1, 0, 0, 0, 58, 412, 1, 0, 0, 0, 60, 443, 1, 0, 0, 0, 62, 455, 1, 0, 0, 0, 64, 569, 1, 0, 0, 0, 66, 587, 1, 0, 0, 0, 68, 637, 1, 0, 0, 0, 70, 671, 1, 0, 0, 0, 72, 705, 1, 0, 0, 0, 74, 707, 1, 0, 0, 0, 76, 716, 1, 0, 0, 0, 78, 725, 1, 0, 0, 0, 80, 745, 1, 0, 0, 0, 82, 747, 1, 0, 0, 0, 84, 753, 1, 0, 0, 0, 86, 757, 1, 0, 0, 0, 88, 779, 1, 0, 0, 0, 90, 781, 1, 0, 0, 0, 92, 783, 1, 0, 0, 0, 94, 785, 1, 0, 0, 0, 96, 787, 1, 0, 0, 0, 98, 795, 1, 0, 0, 0, 100, 803, 1, 0, 0, 0, 102, 971, 1, 0, 0, 0, 104, 978, 1, 0, 0, 0, 106, 988, 1, 0, 0, 0, 108, 990, 1, 0, 0, 0, 110, 1003, 1, 0, 0, 0, 112, 1005, 1, 0, 0, 0, 114, 1012, 1, 0, 0, 0, 116, 1014, 1, 0, 0, 0, 118, 1016, 1, 0, 0, 0, 120, 1027, 1, 0, 0, 0, 122, 1035, 1, 0, 0, 0, 124, 1040, 1, 0, 0, 0, 126, 127, 7, 0, 0, 0, 127, 1, 1, 0, 0, 0, 128, 131, 3, 24, 12, 0, 129, 131, 3, 26, 13, 0, 130, 128, 1, 0, 0, 0, 130, 129, 1, 0, 0, 0, 131, 3, 1, 0, 0, 0, 132, 133, 7, 1, 0, 0, 133, 5, 1, 0, 0, 0, 134, 135, 5, 176, 0, 0, 135, 140, 5, 167, 0, 0, 136, 141, 5, 179, 0, 0, 137, 138, 5, 55, 0, 0, 138, 139, 5, 179, 0, 0, 139, 141, 5, 56, 0, 0, 140, 136, 1, 0, 0, 0, 140, 137, 1, 0, 0, 0, 141, 7, 1, 0, 0, 0, 142, 147, 3, 32, 16, 0, 143, 147, 3, 64, 32, 0, 144, 147, 5, 47, 0, 0, 145, 147, 5, 48, 0, 0, 146, 142, 1, 0, 0, 0, 146, 143, 1, 0, 0, 0, 146, 144, 1, 0, 0, 0, 146, 145, 1, 0, 0, 0, 147, 148, 1, 0, 0, 0, 148, 149, 3, 6, 3, 0, 149, 9, 1, 0, 0, 0, 150, 151, 3, 6, 3, 0, 151, 152, 5, 178, 0, 0, 152, 153, 3, 6, 3, 0, 153, 11, 1, 0, 0, 0, 154, 155, 3, 6, 3, 0, 155, 156, 3, 8, 4, 0, 156, 13, 1, 0, 0, 0, 157, 161, 3, 12, 6, 0, 158, 161, 3, 8, 4, 0, 159, 161, 3, 10, 5, 0, 160, 157, 1, 0, 0, 0, 160, 158, 1, 0, 0, 0, 160, 159, 1, 0, 0, 0, 161, 15, 1, 0, 0, 0, 162, 167, 3, 14, 7, 0, 163, 164, 5, 171, 0, 0, 164, 166, 3, 14, 7, 0, 165, 163, 1, 0, 0, 0, 166, 169, 1, 0, 0, 0, 167, 165, 1, 0, 0, 0, 167, 168, 1, 0, 0, 0, 168, 17, 1, 0, 0, 0, 169, 167, 1, 0, 0, 0, 170, 171, 5, 161, 0, 0, 171, 176, 3, 22, 11, 0, 172, 173, 5, 166, 0, 0, 173, 175, 3, 22, 11, 0, 174, 172, 1, 0, 0, 0, 175, 178, 1, 0, 0, 0, 176, 174, 1, 0, 0, 0, 176, 177, 1, 0, 0, 0, 177, 180, 1, 0, 0, 0, 178, 176, 1, 0, 0, 0, 179, 181, 5, 166, 0, 0, 180, 179, 1, 0, 0, 0, 180, 181, 1, 0, 0, 0, 181, 182, 1, 0, 0, 0, 182, 194, 5, 162, 0, 0, 183, 188, 5, 177, 0, 0, 184, 185, 5, 61, 0, 0, 185, 186, 3, 16, 8, 0, 186, 187, 5, 62, 0, 0, 187, 189, 1, 0, 0, 0, 188, 184, 1, 0, 0, 0, 188, 189, 1, 0, 0, 0, 189, 190, 1, 0, 0, 0, 190, 191, 5, 55, 0, 0, 191, 192, 3, 16, 8, 0, 192, 193, 5, 56, 0, 0, 193, 195, 1, 0, 0, 0, 194, 183, 1, 0, 0, 0, 194, 195, 1, 0, 0, 0, 195, 19, 1, 0, 0, 0, 196, 197, 5, 163, 0, 0, 197, 202, 3, 22, 11, 0, 198, 199, 5, 166, 0, 0, 199, 201, 3, 22, 11, 0, 200, 198, 1, 0, 0, 0, 201, 204, 1, 0, 0, 0, 202, 200, 1, 0, 0, 0, 202, 203, 1, 0, 0, 0, 203, 206, 1, 0, 0, 0, 204, 202, 1, 0, 0, 0, 205, 207, 5, 166, 0, 0, 206, 205, 1, 0, 0, 0, 206, 207, 1, 0, 0, 0, 207, 208, 1, 0, 0, 0, 208, 209, 5, 164, 0, 0, 209, 21, 1, 0, 0, 0, 210, 215, 3, 32, 16, 0, 211, 212, 5, 165, 0, 0, 212, 214, 3, 32, 16, 0, 213, 211, 1, 0, 0, 0, 214, 217, 1, 0, 0, 0, 215, 213, 1, 0, 0, 0, 215, 216, 1, 0, 0, 0, 216, 23, 1, 0, 0, 0, 217, 215, 1, 0, 0, 0, 218, 219, 6, 12, -1, 0, 219, 220, 3, 32, 16, 0, 220, 226, 1, 0, 0, 0, 221, 222, 10, 2, 0, 0, 222, 223, 7, 2, 0, 0, 223, 225, 3, 24, 12, 3, 224, 221, 1, 0, 0, 0, 225, 228, 1, 0, 0, 0, 226, 224, 1, 0, 0, 0, 226, 227, 1, 0, 0, 0, 227, 25, 1, 0, 0, 0, 228, 226, 1, 0, 0, 0, 229, 267, 3, 28, 14, 0, 230, 231, 5, 61, 0, 0, 231, 232, 3, 28, 14, 0, 232, 233, 5, 62, 0, 0, 233, 267, 1, 0, 0, 0, 234, 235, 5, 55, 0, 0, 235, 236, 3, 28, 14, 0, 236, 237, 5, 56, 0, 0, 237, 267, 1, 0, 0, 0, 238, 239, 5, 57, 0, 0, 239, 240, 3, 28, 14, 0, 240, 241, 5, 58, 0, 0, 241, 267, 1, 0, 0, 0, 242, 243, 5, 78, 0, 0, 243, 244, 5, 61, 0, 0, 244, 245, 3, 28, 14, 0, 245, 246, 5, 79, 0, 0, 246, 247, 5, 62, 0, 0, 247, 267, 1, 0, 0, 0, 248, 249, 5, 78, 0, 0, 249, 250, 5, 57, 0, 0, 250, 251, 3, 28, 14, 0, 251, 252, 5, 79, 0, 0, 252, 253, 5, 58, 0, 0, 253, 267, 1, 0, 0, 0, 254, 255, 5, 80, 0, 0, 255, 256, 5, 61, 0, 0, 256, 257, 3, 28, 14, 0, 257, 258, 5, 81, 0, 0, 258, 259, 5, 62, 0, 0, 259, 267, 1, 0, 0, 0, 260, 261, 5, 80, 0, 0, 261, 262, 5, 57, 0, 0, 262, 263, 3, 28, 14, 0, 263, 264, 5, 81, 0, 0, 264, 265, 5, 58, 0, 0, 265, 267, 1, 0, 0, 0, 266, 229, 1, 0, 0, 0, 266, 230, 1, 0, 0, 0, 266, 234, 1, 0, 0, 0, 266, 238, 1, 0, 0, 0, 266, 242, 1, 0, 0, 0, 266, 248, 1, 0, 0, 0, 266, 254, 1, 0, 0, 0, 266, 260, 1, 0, 0, 0, 267, 27, 1, 0, 0, 0, 268, 269, 3, 24, 12, 0, 269, 270, 5, 171, 0, 0, 270, 275, 3, 24, 12, 0, 271, 272, 5, 171, 0, 0, 272, 274, 3, 24, 12, 0, 273, 271, 1, 0, 0, 0, 274, 277, 1, 0, 0, 0, 275, 273, 1, 0, 0, 0, 275, 276, 1, 0, 0, 0, 276, 289, 1, 0, 0, 0, 277, 275, 1, 0, 0, 0, 278, 279, 3, 24, 12, 0, 279, 280, 5, 170, 0, 0, 280, 285, 3, 24, 12, 0, 281, 282, 5, 170, 0, 0, 282, 284, 3, 24, 12, 0, 283, 281, 1, 0, 0, 0, 284, 287, 1, 0, 0, 0, 285, 283, 1, 0, 0, 0, 285, 286, 1, 0, 0, 0, 286, 289, 1, 0, 0, 0, 287, 285, 1, 0, 0, 0, 288, 268, 1, 0, 0, 0, 288, 278, 1, 0, 0, 0, 289, 29, 1, 0, 0, 0, 290, 291, 3, 32, 16, 0, 291, 292, 7, 3, 0, 0, 292, 293, 3, 32, 16, 0, 293, 31, 1, 0, 0, 0, 294, 295, 3, 34, 17, 0, 295, 33, 1, 0, 0, 0, 296, 297, 6, 17, -1, 0, 297, 298, 3, 36, 18, 0, 298, 304, 1, 0, 0, 0, 299, 300, 10, 2, 0, 0, 300, 301, 7, 4, 0, 0, 301, 303, 3, 34, 17, 3, 302, 299, 1, 0, 0, 0, 303, 306, 1, 0, 0, 0, 304, 302, 1, 0, 0, 0, 304, 305, 1, 0, 0, 0, 305, 35, 1, 0, 0, 0, 306, 304, 1, 0, 0, 0, 307, 308, 6, 18, -1, 0, 308, 309, 3, 40, 20, 0, 309, 315, 1, 0, 0, 0, 310, 311, 10, 2, 0, 0, 311, 312, 7, 5, 0, 0, 312, 314, 3, 36, 18, 3, 313, 310, 1, 0, 0, 0, 314, 317, 1, 0, 0, 0, 315, 313, 1, 0, 0, 0, 315, 316, 1, 0, 0, 0, 316, 37, 1, 0, 0, 0, 317, 315, 1, 0, 0, 0, 318, 319, 6, 19, -1, 0, 319, 320, 3, 42, 21, 0, 320, 326, 1, 0, 0, 0, 321, 322, 10, 2, 0, 0, 322, 323, 7, 5, 0, 0, 323, 325, 3, 38, 19, 3, 324, 321, 1, 0, 0, 0, 325, 328, 1, 0, 0, 0, 326, 324, 1, 0, 0, 0, 326, 327, 1, 0, 0, 0, 327, 39, 1, 0, 0, 0, 328, 326, 1, 0, 0, 0, 329, 330, 7, 4, 0, 0, 330, 337, 3, 40, 20, 0, 331, 333, 3, 44, 22, 0, 332, 331, 1, 0, 0, 0, 333, 334, 1, 0, 0, 0, 334, 332, 1, 0, 0, 0, 334, 335, 1, 0, 0, 0, 335, 337, 1, 0, 0, 0, 336, 329, 1, 0, 0, 0, 336, 332, 1, 0, 0, 0, 337, 41, 1, 0, 0, 0, 338, 339, 7, 4, 0, 0, 339, 348, 3, 42, 21, 0, 340, 344, 3, 44, 22, 0, 341, 343, 3, 46, 23, 0, 342, 341, 1, 0, 0, 0, 343, 346, 1, 0, 0, 0, 344, 342, 1, 0, 0, 0, 344, 345, 1, 0, 0, 0, 345, 348, 1, 0, 0, 0, 346, 344, 1, 0, 0, 0, 347, 338, 1, 0, 0, 0, 347, 340, 1, 0, 0, 0, 348, 43, 1, 0, 0, 0, 349, 353, 3, 56, 28, 0, 350, 352, 3, 48, 24, 0, 351, 350, 1, 0, 0, 0, 352, 355, 1, 0, 0, 0, 353, 351, 1, 0, 0, 0, 353, 354, 1, 0, 0, 0, 354, 45, 1, 0, 0, 0, 355, 353, 1, 0, 0, 0, 356, 360, 3, 58, 29, 0, 357, 359, 3, 48, 24, 0, 358, 357, 1, 0, 0, 0, 359, 362, 1, 0, 0, 0, 360, 358, 1, 0, 0, 0, 360, 361, 1, 0, 0, 0, 361, 47, 1, 0, 0, 0, 362, 360, 1, 0, 0, 0, 363, 367, 5, 189, 0, 0, 364, 367, 3, 50, 25, 0, 365, 367, 3, 4, 2, 0, 366, 363, 1, 0, 0, 0, 366, 364, 1, 0, 0, 0, 366, 365, 1, 0, 0, 0, 367, 49, 1, 0, 0, 0, 368, 374, 5, 65, 0, 0, 369, 375, 3, 54, 27, 0, 370, 375, 3, 52, 26, 0, 371, 372, 3, 54, 27, 0, 372, 373, 3, 52, 26, 0, 373, 375, 1, 0, 0, 0, 374, 369, 1, 0, 0, 0, 374, 370, 1, 0, 0, 0, 374, 371, 1, 0, 0, 0, 375, 51, 1, 0, 0, 0, 376, 377, 5, 167, 0, 0, 377, 380, 5, 55, 0, 0, 378, 381, 3, 32, 16, 0, 379, 381, 3, 30, 15, 0, 380, 378, 1, 0, 0, 0, 380, 379, 1, 0, 0, 0, 381, 382, 1, 0, 0, 0, 382, 383, 5, 56, 0, 0, 383, 53, 1, 0, 0, 0, 384, 385, 5, 168, 0, 0, 385, 388, 5, 55, 0, 0, 386, 389, 3, 32, 16, 0, 387, 389, 3, 30, 15, 0, 388, 386, 1, 0, 0, 0, 388, 387, 1, 0, 0, 0, 389, 390, 1, 0, 0, 0, 390, 391, 5, 56, 0, 0, 391, 55, 1, 0, 0, 0, 392, 393, 6, 28, -1, 0, 393, 394, 3, 60, 30, 0, 394, 409, 1, 0, 0, 0, 395, 396, 10, 2, 0, 0, 396, 402, 5, 168, 0, 0, 397, 403, 3, 80, 40, 0, 398, 399, 5, 55, 0, 0, 399, 400, 3, 32, 16, 0, 400, 401, 5, 56, 0, 0, 401, 403, 1, 0, 0, 0, 402, 397, 1, 0, 0, 0, 402, 398, 1, 0, 0, 0, 403, 405, 1, 0, 0, 0, 404, 406, 3, 118, 59, 0, 405, 404, 1, 0, 0, 0, 405, 406, 1, 0, 0, 0, 406, 408, 1, 0, 0, 0, 407, 395, 1, 0, 0, 0, 408, 411, 1, 0, 0, 0, 409, 407, 1, 0, 0, 0, 409, 410, 1, 0, 0, 0, 410, 57, 1, 0, 0, 0, 411, 409, 1, 0, 0, 0, 412, 413, 6, 29, -1, 0, 413, 414, 3, 62, 31, 0, 414, 429, 1, 0, 0, 0, 415, 416, 10, 2, 0, 0, 416, 422, 5, 168, 0, 0, 417, 423, 3, 80, 40, 0, 418, 419, 5, 55, 0, 0, 419, 420, 3, 32, 16, 0, 420, 421, 5, 56, 0, 0, 421, 423, 1, 0, 0, 0, 422, 417, 1, 0, 0, 0, 422, 418, 1, 0, 0, 0, 423, 425, 1, 0, 0, 0, 424, 426, 3, 118, 59, 0, 425, 424, 1, 0, 0, 0, 425, 426, 1, 0, 0, 0, 426, 428, 1, 0, 0, 0, 427, 415, 1, 0, 0, 0, 428, 431, 1, 0, 0, 0, 429, 427, 1, 0, 0, 0, 429, 430, 1, 0, 0, 0, 430, 59, 1, 0, 0, 0, 431, 429, 1, 0, 0, 0, 432, 444, 3, 64, 32, 0, 433, 444, 3, 66, 33, 0, 434, 444, 3, 68, 34, 0, 435, 444, 3, 70, 35, 0, 436, 444, 3, 72, 36, 0, 437, 444, 3, 102, 51, 0, 438, 444, 3, 80, 40, 0, 439, 444, 3, 86, 43, 0, 440, 444, 3, 88, 44, 0, 441, 444, 3, 18, 9, 0, 442, 444, 3, 20, 10, 0, 443, 432, 1, 0, 0, 0, 443, 433, 1, 0, 0, 0, 443, 434, 1, 0, 0, 0, 443, 435, 1, 0, 0, 0, 443, 436, 1, 0, 0, 0, 443, 437, 1, 0, 0, 0, 443, 438, 1, 0, 0, 0, 443, 439, 1, 0, 0, 0, 443, 440, 1, 0, 0, 0, 443, 441, 1, 0, 0, 0, 443, 442, 1, 0, 0, 0, 444, 61, 1, 0, 0, 0, 445, 456, 3, 64, 32, 0, 446, 456, 3, 66, 33, 0, 447, 456, 3, 68, 34, 0, 448, 456, 3, 70, 35, 0, 449, 456, 3, 72, 36, 0, 450, 456, 3, 80, 40, 0, 451, 456, 3, 86, 43, 0, 452, 456, 3, 88, 44, 0, 453, 456, 3, 18, 9, 0, 454, 456, 3, 20, 10, 0, 455, 445, 1, 0, 0, 0, 455, 446, 1, 0, 0, 0, 455, 447, 1, 0, 0, 0, 455, 448, 1, 0, 0, 0, 455, 449, 1, 0, 0, 0, 455, 450, 1, 0, 0, 0, 455, 451, 1, 0, 0, 0, 455, 452, 1, 0, 0, 0, 455, 453, 1, 0, 0, 0, 455, 454, 1, 0, 0, 0, 456, 63, 1, 0, 0, 0, 457, 458, 5, 51, 0, 0, 458, 459, 3, 32, 16, 0, 459, 460, 5, 52, 0, 0, 460, 570, 1, 0, 0, 0, 461, 462, 5, 53, 0, 0, 462, 463, 3, 32, 16, 0, 463, 464, 5, 54, 0, 0, 464, 570, 1, 0, 0, 0, 465, 466, 5, 55, 0, 0, 466, 467, 3, 32, 16, 0, 467, 468, 5, 56, 0, 0, 468, 570, 1, 0, 0, 0, 469, 470, 5, 57, 0, 0, 470, 471, 3, 32, 16, 0, 471, 472, 5, 58, 0, 0, 472, 570, 1, 0, 0, 0, 473, 474, 5, 59, 0, 0, 474, 475, 3, 32, 16, 0, 475, 476, 5, 60, 0, 0, 476, 570, 1, 0, 0, 0, 477, 478, 5, 61, 0, 0, 478, 479, 3, 32, 16, 0, 479, 480, 5, 62, 0, 0, 480, 570, 1, 0, 0, 0, 481, 482, 5, 63, 0, 0, 482, 483, 3, 32, 16, 0, 483, 484, 5, 64, 0, 0, 484, 570, 1, 0, 0, 0, 485, 486, 5, 78, 0, 0, 486, 487, 5, 51, 0, 0, 487, 488, 3, 32, 16, 0, 488, 489, 5, 79, 0, 0, 489, 490, 5, 52, 0, 0, 490, 570, 1, 0, 0, 0, 491, 492, 5, 78, 0, 0, 492, 493, 5, 53, 0, 0, 493, 494, 3, 32, 16, 0, 494, 495, 5, 79, 0, 0, 495, 496, 5, 54, 0, 0, 496, 570, 1, 0, 0, 0, 497, 498, 5, 78, 0, 0, 498, 499, 5, 55, 0, 0, 499, 500, 3, 32, 16, 0, 500, 501, 5, 79, 0, 0, 501, 502, 5, 56, 0, 0, 502, 570, 1, 0, 0, 0, 503, 504, 5, 78, 0, 0, 504, 505, 5, 57, 0, 0, 505, 506, 3, 32, 16, 0, 506, 507, 5, 79, 0, 0, 507, 508, 5, 58, 0, 0, 508, 570, 1, 0, 0, 0, 509, 510, 5, 78, 0, 0, 510, 511, 5, 59, 0, 0, 511, 512, 3, 32, 16, 0, 512, 513, 5, 79, 0, 0, 513, 514, 5, 60, 0, 0, 514, 570, 1, 0, 0, 0, 515, 516, 5, 78, 0, 0, 516, 517, 5, 61, 0, 0, 517, 518, 3, 32, 16, 0, 518, 519, 5, 79, 0, 0, 519, 520, 5, 62, 0, 0, 520, 570, 1, 0, 0, 0, 521, 522, 5, 78, 0, 0, 522, 523, 5, 63, 0, 0, 523, 524, 3, 32, 16, 0, 524, 525, 5, 79, 0, 0, 525, 526, 5, 64, 0, 0, 526, 570, 1, 0, 0, 0, 527, 528, 5, 80, 0, 0, 528, 529, 5, 51, 0, 0, 529, 530, 3, 32, 16, 0, 530, 531, 5, 81, 0, 0, 531, 532, 5, 52, 0, 0, 532, 570, 1, 0, 0, 0, 533, 534, 5, 80, 0, 0, 534, 535, 5, 53, 0, 0, 535, 536, 3, 32, 16, 0, 536, 537, 5, 81, 0, 0, 537, 538, 5, 54, 0, 0, 538, 570, 1, 0, 0, 0, 539, 540, 5, 80, 0, 0, 540, 541, 5, 55, 0, 0, 541, 542, 3, 32, 16, 0, 542, 543, 5, 81, 0, 0, 543, 544, 5, 56, 0, 0, 544, 570, 1, 0, 0, 0, 545, 546, 5, 80, 0, 0, 546, 547, 5, 57, 0, 0, 547, 548, 3, 32, 16, 0, 548, 549, 5, 81, 0, 0, 549, 550, 5, 58, 0, 0, 550, 570, 1, 0, 0, 0, 551, 552, 5, 80, 0, 0, 552, 553, 5, 59, 0, 0, 553, 554, 3, 32, 16, 0, 554, 555, 5, 81, 0, 0, 555, 556, 5, 60, 0, 0, 556, 570, 1, 0, 0, 0, 557, 558, 5, 80, 0, 0, 558, 559, 5, 61, 0, 0, 559, 560, 3, 32, 16, 0, 560, 561, 5, 81, 0, 0, 561, 562, 5, 62, 0, 0, 562, 570, 1, 0, 0, 0, 563, 564, 5, 80, 0, 0, 564, 565, 5, 63, 0, 0, 565, 566, 3, 32, 16, 0, 566, 567, 5, 81, 0, 0, 567, 568, 5, 64, 0, 0, 568, 570, 1, 0, 0, 0, 569, 457, 1, 0, 0, 0, 569, 461, 1, 0, 0, 0, 569, 465, 1, 0, 0, 0, 569, 469, 1, 0, 0, 0, 569, 473, 1, 0, 0, 0, 569, 477, 1, 0, 0, 0, 569, 481, 1, 0, 0, 0, 569, 485, 1, 0, 0, 0, 569, 491, 1, 0, 0, 0, 569, 497, 1, 0, 0, 0, 569, 503, 1, 0, 0, 0, 569, 509, 1, 0, 0, 0, 569, 515, 1, 0, 0, 0, 569, 521, 1, 0, 0, 0, 569, 527, 1, 0, 0, 0, 569, 533, 1, 0, 0, 0, 569, 539, 1, 0, 0, 0, 569, 545, 1, 0, 0, 0, 569, 551, 1, 0, 0, 0, 569, 557, 1, 0, 0, 0, 569, 563, 1, 0, 0, 0, 570, 65, 1, 0, 0, 0, 571, 572, 5, 69, 0, 0, 572, 573, 3, 32, 16, 0, 573, 574, 5, 69, 0, 0, 574, 588, 1, 0, 0, 0, 575, 576, 5, 78, 0, 0, 576, 577, 5, 69, 0, 0, 577, 578, 3, 32, 16, 0, 578, 579, 5, 79, 0, 0, 579, 580, 5, 69, 0, 0, 580, 588, 1, 0, 0, 0, 581, 582, 5, 80, 0, 0, 582, 583, 5, 69, 0, 0, 583, 584, 3, 32, 16, 0, 584, 585, 5, 81, 0, 0, 585, 586, 5, 69, 0, 0, 586, 588, 1, 0, 0, 0, 587, 571, 1, 0, 0, 0, 587, 575, 1, 0, 0, 0, 587, 581, 1, 0, 0, 0, 588, 67, 1, 0, 0, 0, 589, 590, 5, 65, 0, 0, 590, 591, 3, 32, 16, 0, 591, 592, 5, 65, 0, 0, 592, 638, 1, 0, 0, 0, 593, 594, 5, 66, 0, 0, 594, 595, 3, 32, 16, 0, 595, 596, 5, 67, 0, 0, 596, 638, 1, 0, 0, 0, 597, 598, 5, 68, 0, 0, 598, 599, 3, 32, 16, 0, 599, 600, 5, 68, 0, 0, 600, 638, 1, 0, 0, 0, 601, 602, 5, 78, 0, 0, 602, 603, 5, 65, 0, 0, 603, 604, 3, 32, 16, 0, 604, 605, 5, 79, 0, 0, 605, 606, 5, 65, 0, 0, 606, 638, 1, 0, 0, 0, 607, 608, 5, 78, 0, 0, 608, 609, 5, 66, 0, 0, 609, 610, 3, 32, 16, 0, 610, 611, 5, 79, 0, 0, 611, 612, 5, 67, 0, 0, 612, 638, 1, 0, 0, 0, 613, 614, 5, 78, 0, 0, 614, 615, 5, 68, 0, 0, 615, 616, 3, 32, 16, 0, 616, 617, 5, 79, 0, 0, 617, 618, 5, 68, 0, 0, 618, 638, 1, 0, 0, 0, 619, 620, 5, 80, 0, 0, 620, 621, 5, 65, 0, 0, 621, 622, 3, 32, 16, 0, 622, 623, 5, 81, 0, 0, 623, 624, 5, 65, 0, 0, 624, 638, 1, 0, 0, 0, 625, 626, 5, 80, 0, 0, 626, 627, 5, 66, 0, 0, 627, 628, 3, 32, 16, 0, 628, 629, 5, 81, 0, 0, 629, 630, 5, 67, 0, 0, 630, 638, 1, 0, 0, 0, 631, 632, 5, 80, 0, 0, 632, 633, 5, 68, 0, 0, 633, 634, 3, 32, 16, 0, 634, 635, 5, 81, 0, 0, 635, 636, 5, 68, 0, 0, 636, 638, 1, 0, 0, 0, 637, 589, 1, 0, 0, 0, 637, 593, 1, 0, 0, 0, 637, 597, 1, 0, 0, 0, 637, 601, 1, 0, 0, 0, 637, 607, 1, 0, 0, 0, 637, 613, 1, 0, 0, 0, 637, 619, 1, 0, 0, 0, 637, 625, 1, 0, 0, 0, 637, 631, 1, 0, 0, 0, 638, 69, 1, 0, 0, 0, 639, 640, 5, 70, 0, 0, 640, 641, 3, 32, 16, 0, 641, 642, 5, 71, 0, 0, 642, 672, 1, 0, 0, 0, 643, 644, 5, 72, 0, 0, 644, 645, 3, 32, 16, 0, 645, 646, 5, 73, 0, 0, 646, 672, 1, 0, 0, 0, 647, 648, 5, 78, 0, 0, 648, 649, 5, 70, 0, 0, 649, 650, 3, 32, 16, 0, 650, 651, 5, 79, 0, 0, 651, 652, 5, 71, 0, 0, 652, 672, 1, 0, 0, 0, 653, 654, 5, 78, 0, 0, 654, 655, 5, 72, 0, 0, 655, 656, 3, 32, 16, 0, 656, 657, 5, 79, 0, 0, 657, 658, 5, 73, 0, 0, 658, 672, 1, 0, 0, 0, 659, 660, 5, 80, 0, 0, 660, 661, 5, 70, 0, 0, 661, 662, 3, 32, 16, 0, 662, 663, 5, 81, 0, 0, 663, 664, 5, 71, 0, 0, 664, 672, 1, 0, 0, 0, 665, 666, 5, 80, 0, 0, 666, 667, 5, 72, 0, 0, 667, 668, 3, 32, 16, 0, 668, 669, 5, 81, 0, 0, 669, 670, 5, 73, 0, 0, 670, 672, 1, 0, 0, 0, 671, 639, 1, 0, 0, 0, 671, 643, 1, 0, 0, 0, 671, 647, 1, 0, 0, 0, 671, 653, 1, 0, 0, 0, 671, 659, 1, 0, 0, 0, 671, 665, 1, 0, 0, 0, 672, 71, 1, 0, 0, 0, 673, 674, 5, 74, 0, 0, 674, 675, 3, 32, 16, 0, 675, 676, 5, 75, 0, 0, 676, 706, 1, 0, 0, 0, 677, 678, 5, 76, 0, 0, 678, 679, 3, 32, 16, 0, 679, 680, 5, 77, 0, 0, 680, 706, 1, 0, 0, 0, 681, 682, 5, 78, 0, 0, 682, 683, 5, 74, 0, 0, 683, 684, 3, 32, 16, 0, 684, 685, 5, 79, 0, 0, 685, 686, 5, 75, 0, 0, 686, 706, 1, 0, 0, 0, 687, 688, 5, 78, 0, 0, 688, 689, 5, 76, 0, 0, 689, 690, 3, 32, 16, 0, 690, 691, 5, 79, 0, 0, 691, 692, 5, 77, 0, 0, 692, 706, 1, 0, 0, 0, 693, 694, 5, 80, 0, 0, 694, 695, 5, 74, 0, 0, 695, 696, 3, 32, 16, 0, 696, 697, 5, 81, 0, 0, 697, 698, 5, 75, 0, 0, 698, 706, 1, 0, 0, 0, 699, 700, 5, 80, 0, 0, 700, 701, 5, 76, 0, 0, 701, 702, 3, 32, 16, 0, 702, 703, 5, 81, 0, 0, 703, 704, 5, 77, 0, 0, 704, 706, 1, 0, 0, 0, 705, 673, 1, 0, 0, 0, 705, 677, 1, 0, 0, 0, 705, 681, 1, 0, 0, 0, 705, 687, 1, 0, 0, 0, 705, 693, 1, 0, 0, 0, 705, 699, 1, 0, 0, 0, 706, 73, 1, 0, 0, 0, 707, 708, 3, 0, 0, 0, 708, 709, 5, 55, 0, 0, 709, 710, 3, 32, 16, 0, 710, 711, 5, 56, 0, 0, 711, 75, 1, 0, 0, 0, 712, 717, 5, 176, 0, 0, 713, 717, 5, 191, 0, 0, 714, 717, 5, 192, 0, 0, 715, 717, 3, 74, 37, 0, 716, 712, 1, 0, 0, 0, 716, 713, 1, 0, 0, 0, 716, 714, 1, 0, 0, 0, 716, 715, 1, 0, 0, 0, 717, 719, 1, 0, 0, 0, 718, 720, 3, 118, 59, 0, 719, 718, 1, 0, 0, 0, 719, 720, 1, 0, 0, 0, 720, 77, 1, 0, 0, 0, 721, 726, 5, 176, 0, 0, 722, 726, 5, 191, 0, 0, 723, 726, 5, 192, 0, 0, 724, 726, 3, 74, 37, 0, 725, 721, 1, 0, 0, 0, 725, 722, 1, 0, 0, 0, 725, 723, 1, 0, 0, 0, 725, 724, 1, 0, 0, 0, 726, 735, 1, 0, 0, 0, 727, 728, 3, 120, 60, 0, 728, 729, 3, 118, 59, 0, 729, 736, 1, 0, 0, 0, 730, 731, 3, 118, 59, 0, 731, 732, 3, 120, 60, 0, 732, 736, 1, 0, 0, 0, 733, 736, 3, 118, 59, 0, 734, 736, 3, 120, 60, 0, 735, 727, 1, 0, 0, 0, 735, 730, 1, 0, 0, 0, 735, 733, 1, 0, 0, 0, 735, 734, 1, 0, 0, 0, 735, 736, 1, 0, 0, 0, 736, 79, 1, 0, 0, 0, 737, 746, 3, 78, 39, 0, 738, 746, 5, 193, 0, 0, 739, 746, 5, 179, 0, 0, 740, 746, 5, 190, 0, 0, 741, 746, 5, 180, 0, 0, 742, 746, 5, 173, 0, 0, 743, 746, 3, 82, 41, 0, 744, 746, 5, 194, 0, 0, 745, 737, 1, 0, 0, 0, 745, 738, 1, 0, 0, 0, 745, 739, 1, 0, 0, 0, 745, 740, 1, 0, 0, 0, 745, 741, 1, 0, 0, 0, 745, 742, 1, 0, 0, 0, 745, 743, 1, 0, 0, 0, 745, 744, 1, 0, 0, 0, 746, 81, 1, 0, 0, 0, 747, 748, 5, 154, 0, 0, 748, 749, 5, 55, 0, 0, 749, 750, 3, 84, 42, 0, 750, 751, 5, 56, 0, 0, 751, 83, 1, 0, 0, 0, 752, 754, 7, 6, 0, 0, 753, 752, 1, 0, 0, 0, 754, 755, 1, 0, 0, 0, 755, 753, 1, 0, 0, 0, 755, 756, 1, 0, 0, 0, 756, 85, 1, 0, 0, 0, 757, 758, 5, 150, 0, 0, 758, 759, 5, 55, 0, 0, 759, 760, 3, 32, 16, 0, 760, 761, 5, 56, 0, 0, 761, 762, 5, 55, 0, 0, 762, 763, 3, 32, 16, 0, 763, 764, 5, 56, 0, 0, 764, 87, 1, 0, 0, 0, 765, 766, 5, 55, 0, 0, 766, 767, 3, 32, 16, 0, 767, 768, 5, 152, 0, 0, 768, 769, 3, 32, 16, 0, 769, 770, 5, 56, 0, 0, 770, 780, 1, 0, 0, 0, 771, 772, 5, 151, 0, 0, 772, 773, 5, 55, 0, 0, 773, 774, 3, 32, 16, 0, 774, 775, 5, 56, 0, 0, 775, 776, 5, 55, 0, 0, 776, 777, 3, 32, 16, 0, 777, 778, 5, 56, 0, 0, 778, 780, 1, 0, 0, 0, 779, 765, 1, 0, 0, 0, 779, 771, 1, 0, 0, 0, 780, 89, 1, 0, 0, 0, 781, 782, 7, 7, 0, 0, 782, 91, 1, 0, 0, 0, 783, 784, 7, 8, 0, 0, 784, 93, 1, 0, 0, 0, 785, 786, 7, 9, 0, 0, 786, 95, 1, 0, 0, 0, 787, 788, 7, 10, 0, 0, 788, 97, 1, 0, 0, 0, 789, 796, 3, 90, 45, 0, 790, 791, 5, 155, 0, 0, 791, 792, 5, 55, 0, 0, 792, 793, 3, 94, 47, 0, 793, 794, 5, 56, 0, 0, 794, 796, 1, 0, 0, 0, 795, 789, 1, 0, 0, 0, 795, 790, 1, 0, 0, 0, 796, 99, 1, 0, 0, 0, 797, 804, 3, 92, 46, 0, 798, 799, 5, 155, 0, 0, 799, 800, 5, 55, 0, 0, 800, 801, 3, 96, 48, 0, 801, 802, 5, 56, 0, 0, 802, 804, 1, 0, 0, 0, 803, 797, 1, 0, 0, 0, 803, 798, 1, 0, 0, 0, 804, 101, 1, 0, 0, 0, 805, 818, 3, 98, 49, 0, 806, 808, 3, 118, 59, 0, 807, 806, 1, 0, 0, 0, 807, 808, 1, 0, 0, 0, 808, 810, 1, 0, 0, 0, 809, 811, 3, 120, 60, 0, 810, 809, 1, 0, 0, 0, 810, 811, 1, 0, 0, 0, 811, 819, 1, 0, 0, 0, 812, 814, 3, 120, 60, 0, 813, 812, 1, 0, 0, 0, 813, 814, 1, 0, 0, 0, 814, 816, 1, 0, 0, 0, 815, 817, 3, 118, 59, 0, 816, 815, 1, 0, 0, 0, 816, 817, 1, 0, 0, 0, 817, 819, 1, 0, 0, 0, 818, 807, 1, 0, 0, 0, 818, 813, 1, 0, 0, 0, 819, 841, 1, 0, 0, 0, 820, 822, 5, 78, 0, 0, 821, 820, 1, 0, 0, 0, 821, 822, 1, 0, 0, 0, 822, 823, 1, 0, 0, 0, 823, 824, 5, 51, 0, 0, 824, 826, 3, 110, 55, 0, 825, 827, 5, 79, 0, 0, 826, 825, 1, 0, 0, 0, 826, 827, 1, 0, 0, 0, 827, 828, 1, 0, 0, 0, 828, 829, 5, 52, 0, 0, 829, 842, 1, 0, 0, 0, 830, 832, 5, 80, 0, 0, 831, 830, 1, 0, 0, 0, 831, 832, 1, 0, 0, 0, 832, 833, 1, 0, 0, 0, 833, 834, 5, 51, 0, 0, 834, 836, 3, 110, 55, 0, 835, 837, 5, 81, 0, 0, 836, 835, 1, 0, 0, 0, 836, 837, 1, 0, 0, 0, 837, 838, 1, 0, 0, 0, 838, 839, 5, 52, 0, 0, 839, 842, 1, 0, 0, 0, 840, 842, 3, 112, 56, 0, 841, 821, 1, 0, 0, 0, 841, 831, 1, 0, 0, 0, 841, 840, 1, 0, 0, 0, 842, 972, 1, 0, 0, 0, 843, 856, 3, 100, 50, 0, 844, 846, 3, 118, 59, 0, 845, 844, 1, 0, 0, 0, 845, 846, 1, 0, 0, 0, 846, 848, 1, 0, 0, 0, 847, 849, 3, 120, 60, 0, 848, 847, 1, 0, 0, 0, 848, 849, 1, 0, 0, 0, 849, 857, 1, 0, 0, 0, 850, 852, 3, 120, 60, 0, 851, 850, 1, 0, 0, 0, 851, 852, 1, 0, 0, 0, 852, 854, 1, 0, 0, 0, 853, 855, 3, 118, 59, 0, 854, 853, 1, 0, 0, 0, 854, 855, 1, 0, 0, 0, 855, 857, 1, 0, 0, 0, 856, 845, 1, 0, 0, 0, 856, 851, 1, 0, 0, 0, 857, 879, 1, 0, 0, 0, 858, 860, 5, 78, 0, 0, 859, 858, 1, 0, 0, 0, 859, 860, 1, 0, 0, 0, 860, 861, 1, 0, 0, 0, 861, 862, 5, 51, 0, 0, 862, 864, 3, 114, 57, 0, 863, 865, 5, 79, 0, 0, 864, 863, 1, 0, 0, 0, 864, 865, 1, 0, 0, 0, 865, 866, 1, 0, 0, 0, 866, 867, 5, 52, 0, 0, 867, 880, 1, 0, 0, 0, 868, 870, 5, 80, 0, 0, 869, 868, 1, 0, 0, 0, 869, 870, 1, 0, 0, 0, 870, 871, 1, 0, 0, 0, 871, 872, 5, 51, 0, 0, 872, 874, 3, 114, 57, 0, 873, 875, 5, 81, 0, 0, 874, 873, 1, 0, 0, 0, 874, 875, 1, 0, 0, 0, 875, 876, 1, 0, 0, 0, 876, 877, 5, 52, 0, 0, 877, 880, 1, 0, 0, 0, 878, 880, 3, 116, 58, 0, 879, 859, 1, 0, 0, 0, 879, 869, 1, 0, 0, 0, 879, 878, 1, 0, 0, 0, 880, 972, 1, 0, 0, 0, 881, 883, 3, 76, 38, 0, 882, 884, 3, 120, 60, 0, 883, 882, 1, 0, 0, 0, 883, 884, 1, 0, 0, 0, 884, 886, 1, 0, 0, 0, 885, 887, 5, 78, 0, 0, 886, 885, 1, 0, 0, 0, 886, 887, 1, 0, 0, 0, 887, 888, 1, 0, 0, 0, 888, 889, 7, 11, 0, 0, 889, 890, 3, 106, 53, 0, 890, 892, 7, 12, 0, 0, 891, 893, 5, 79, 0, 0, 892, 891, 1, 0, 0, 0, 892, 893, 1, 0, 0, 0, 893, 972, 1, 0, 0, 0, 894, 896, 3, 76, 38, 0, 895, 897, 3, 120, 60, 0, 896, 895, 1, 0, 0, 0, 896, 897, 1, 0, 0, 0, 897, 898, 1, 0, 0, 0, 898, 900, 5, 55, 0, 0, 899, 901, 5, 78, 0, 0, 900, 899, 1, 0, 0, 0, 900, 901, 1, 0, 0, 0, 901, 902, 1, 0, 0, 0, 902, 903, 7, 11, 0, 0, 903, 904, 3, 106, 53, 0, 904, 906, 7, 12, 0, 0, 905, 907, 5, 79, 0, 0, 906, 905, 1, 0, 0, 0, 906, 907, 1, 0, 0, 0, 907, 908, 1, 0, 0, 0, 908, 909, 5, 56, 0, 0, 909, 972, 1, 0, 0, 0, 910, 931, 5, 84, 0, 0, 911, 912, 3, 118, 59, 0, 912, 913, 3, 120, 60, 0, 913, 932, 1, 0, 0, 0, 914, 915, 3, 120, 60, 0, 915, 916, 3, 118, 59, 0, 916, 932, 1, 0, 0, 0, 917, 918, 5, 167, 0, 0, 918, 919, 5, 55, 0, 0, 919, 920, 5, 56, 0, 0, 920, 921, 1, 0, 0, 0, 921, 922, 5, 168, 0, 0, 922, 923, 5, 55, 0, 0, 923, 932, 5, 56, 0, 0, 924, 925, 5, 168, 0, 0, 925, 926, 5, 55, 0, 0, 926, 927, 5, 56, 0, 0, 927, 928, 1, 0, 0, 0, 928, 929, 5, 167, 0, 0, 929, 930, 5, 55, 0, 0, 930, 932, 5, 56, 0, 0, 931, 911, 1, 0, 0, 0, 931, 914, 1, 0, 0, 0, 931, 917, 1, 0, 0, 0, 931, 924, 1, 0, 0, 0, 931, 932, 1, 0, 0, 0, 932, 939, 1, 0, 0, 0, 933, 935, 3, 34, 17, 0, 934, 933, 1, 0, 0, 0, 934, 935, 1, 0, 0, 0, 935, 936, 1, 0, 0, 0, 936, 940, 5, 173, 0, 0, 937, 940, 3, 86, 43, 0, 938, 940, 3, 34, 17, 0, 939, 934, 1, 0, 0, 0, 939, 937, 1, 0, 0, 0, 939, 938, 1, 0, 0, 0, 940, 972, 1, 0, 0, 0, 941, 946, 5, 121, 0, 0, 942, 943, 5, 61, 0, 0, 943, 944, 3, 32, 16, 0, 944, 945, 5, 62, 0, 0, 945, 947, 1, 0, 0, 0, 946, 942, 1, 0, 0, 0, 946, 947, 1, 0, 0, 0, 947, 948, 1, 0, 0, 0, 948, 949, 5, 55, 0, 0, 949, 950, 3, 32, 16, 0, 950, 951, 5, 56, 0, 0, 951, 972, 1, 0, 0, 0, 952, 959, 7, 13, 0, 0, 953, 954, 3, 122, 61, 0, 954, 955, 3, 120, 60, 0, 955, 960, 1, 0, 0, 0, 956, 957, 3, 120, 60, 0, 957, 958, 3, 122, 61, 0, 958, 960, 1, 0, 0, 0, 959, 953, 1, 0, 0, 0, 959, 956, 1, 0, 0, 0, 960, 961, 1, 0, 0, 0, 961, 962, 3, 36, 18, 0, 962, 972, 1, 0, 0, 0, 963, 964, 5, 82, 0, 0, 964, 965, 3, 108, 54, 0, 965, 966, 3, 36, 18, 0, 966, 972, 1, 0, 0, 0, 967, 969, 5, 174, 0, 0, 968, 970, 3, 120, 60, 0, 969, 968, 1, 0, 0, 0, 969, 970, 1, 0, 0, 0, 970, 972, 1, 0, 0, 0, 971, 805, 1, 0, 0, 0, 971, 843, 1, 0, 0, 0, 971, 881, 1, 0, 0, 0, 971, 894, 1, 0, 0, 0, 971, 910, 1, 0, 0, 0, 971, 941, 1, 0, 0, 0, 971, 952, 1, 0, 0, 0, 971, 963, 1, 0, 0, 0, 971, 967, 1, 0, 0, 0, 972, 103, 1, 0, 0, 0, 973, 974, 3, 32, 16, 0, 974, 975, 5, 171, 0, 0, 975, 976, 3, 104, 52, 0, 976, 979, 1, 0, 0, 0, 977, 979, 3, 32, 16, 0, 978, 973, 1, 0, 0, 0, 978, 977, 1, 0, 0, 0, 979, 105, 1, 0, 0, 0, 980, 989, 3, 80, 40, 0, 981, 982, 3, 32, 16, 0, 982, 983, 5, 171, 0, 0, 983, 989, 1, 0, 0, 0, 984, 985, 3, 32, 16, 0, 985, 986, 5, 171, 0, 0, 986, 987, 3, 104, 52, 0, 987, 989, 1, 0, 0, 0, 988, 980, 1, 0, 0, 0, 988, 981, 1, 0, 0, 0, 988, 984, 1, 0, 0, 0, 989, 107, 1, 0, 0, 0, 990, 991, 5, 167, 0, 0, 991, 992, 5, 55, 0, 0, 992, 993, 7, 14, 0, 0, 993, 994, 5, 83, 0, 0, 994, 999, 3, 32, 16, 0, 995, 996, 5, 168, 0, 0, 996, 997, 5, 55, 0, 0, 997, 998, 7, 4, 0, 0, 998, 1000, 5, 56, 0, 0, 999, 995, 1, 0, 0, 0, 999, 1000, 1, 0, 0, 0, 1000, 1001, 1, 0, 0, 0, 1001, 1002, 5, 56, 0, 0, 1002, 109, 1, 0, 0, 0, 1003, 1004, 3, 32, 16, 0, 1004, 111, 1, 0, 0, 0, 1005, 1006, 3, 38, 19, 0, 1006, 113, 1, 0, 0, 0, 1007, 1013, 3, 32, 16, 0, 1008, 1009, 3, 32, 16, 0, 1009, 1010, 5, 171, 0, 0, 1010, 1011, 3, 114, 57, 0, 1011, 1013, 1, 0, 0, 0, 1012, 1007, 1, 0, 0, 0, 1012, 1008, 1, 0, 0, 0, 1013, 115, 1, 0, 0, 0, 1014, 1015, 3, 38, 19, 0, 1015, 117, 1, 0, 0, 0, 1016, 1025, 5, 167, 0, 0, 1017, 1026, 3, 80, 40, 0, 1018, 1021, 5, 55, 0, 0, 1019, 1022, 3, 32, 16, 0, 1020, 1022, 3, 104, 52, 0, 1021, 1019, 1, 0, 0, 0, 1021, 1020, 1, 0, 0, 0, 1022, 1023, 1, 0, 0, 0, 1023, 1024, 5, 56, 0, 0, 1024, 1026, 1, 0, 0, 0, 1025, 1017, 1, 0, 0, 0, 1025, 1018, 1, 0, 0, 0, 1026, 119, 1, 0, 0, 0, 1027, 1033, 5, 168, 0, 0, 1028, 1034, 3, 80, 40, 0, 1029, 1030, 5, 55, 0, 0, 1030, 1031, 3, 32, 16, 0, 1031, 1032, 5, 56, 0, 0, 1032, 1034, 1, 0, 0, 0, 1033, 1028, 1, 0, 0, 0, 1033, 1029, 1, 0, 0, 0, 1034, 121, 1, 0, 0, 0, 1035, 1036, 5, 167, 0, 0, 1036, 1037, 5, 55, 0, 0, 1037, 1038, 3, 30, 15, 0, 1038, 1039, 5, 56, 0, 0, 1039, 123, 1, 0, 0, 0, 1040, 1041, 5, 167, 0, 0, 1041, 1042, 5, 55, 0, 0, 1042, 1043, 3, 30, 15, 0, 1043, 1044, 5, 56, 0, 0, 1044, 125, 1, 0, 0, 0, 92, 130, 140, 146, 160, 167, 176, 180, 188, 194, 202, 206, 215, 226, 266, 275, 285, 288, 304, 315, 326, 334, 336, 344, 347, 353, 360, 366, 374, 380, 388, 402, 405, 409, 422, 425, 429, 443, 455, 569, 587, 637, 671, 705, 716, 719, 725, 735, 745, 755, 779, 795, 803, 807, 810, 813, 816, 818, 821, 826, 831, 836, 841, 845, 848, 851, 854, 856, 859, 864, 869, 874, 879, 883, 886, 892, 896, 900, 906, 931, 934, 939, 946, 959, 969, 971, 978, 988, 999, 1012, 1021, 1025, 1033]
\ No newline at end of file diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/PS.tokens b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PS.tokens new file mode 100755 index 0000000..d71163f --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PS.tokens @@ -0,0 +1,357 @@ +T__0=1 +T__1=2 +T__2=3 +T__3=4 +T__4=5 +T__5=6 +T__6=7 +T__7=8 +T__8=9 +T__9=10 +T__10=11 +T__11=12 +T__12=13 +T__13=14 +T__14=15 +T__15=16 +T__16=17 +T__17=18 +T__18=19 +T__19=20 +T__20=21 +T__21=22 +T__22=23 +T__23=24 +T__24=25 +T__25=26 +T__26=27 +T__27=28 +T__28=29 +T__29=30 +T__30=31 +T__31=32 +T__32=33 +T__33=34 +T__34=35 +T__35=36 +T__36=37 +T__37=38 +T__38=39 +T__39=40 +T__40=41 +T__41=42 +T__42=43 +T__43=44 +WS=45 +DOLLAR_SIGN=46 +ADD=47 +SUB=48 +MUL=49 +DIV=50 +L_PAREN=51 +R_PAREN=52 +L_GROUP=53 +R_GROUP=54 +L_BRACE=55 +R_BRACE=56 +L_BRACE_VISUAL=57 +R_BRACE_VISUAL=58 +L_BRACE_CMD=59 +R_BRACE_CMD=60 +L_BRACKET=61 +R_BRACKET=62 +L_BRACK=63 +R_BRACK=64 +BAR=65 +L_VERT=66 +R_VERT=67 +VERT=68 +NORM=69 +L_FLOOR=70 +R_FLOOR=71 +LL_CORNER=72 +LR_CORNER=73 +L_CEIL=74 +R_CEIL=75 +UL_CORNER=76 +UR_CORNER=77 +L_LEFT=78 +R_RIGHT=79 +ML_LEFT=80 +MR_RIGHT=81 +FUNC_LIM=82 +LIM_APPROACH_SYM=83 +FUNC_INT=84 +FUNC_SUM=85 +FUNC_PROD=86 +FUNC_LOG=87 +FUNC_LN=88 +FUNC_EXP=89 +FUNC_SIN=90 +FUNC_COS=91 +FUNC_TAN=92 +FUNC_CSC=93 +FUNC_SEC=94 +FUNC_COT=95 +FUNC_ARCSIN=96 +FUNC_ARCCOS=97 +FUNC_ARCTAN=98 +FUNC_ARCCSC=99 +FUNC_ARCSEC=100 +FUNC_ARCCOT=101 +FUNC_SINH=102 +FUNC_COSH=103 +FUNC_TANH=104 +FUNC_ARSINH=105 +FUNC_ARCOSH=106 +FUNC_ARTANH=107 +FUNC_ARCSINH=108 +FUNC_ARCCOSH=109 +FUNC_ARCTANH=110 +FUNC_ARSINH_NAME=111 +FUNC_ARCSINH_NAME=112 +FUNC_ARCOSH_NAME=113 +FUNC_ARCCOSH_NAME=114 +FUNC_ARTANH_NAME=115 +FUNC_ARCTANH_NAME=116 +FUNC_GCD_NAME=117 +FUNC_LCM_NAME=118 +FUNC_FLOOR_NAME=119 +FUNC_CEIL_NAME=120 +FUNC_SQRT=121 +FUNC_GCD=122 +FUNC_LCM=123 +FUNC_FLOOR=124 +FUNC_CEIL=125 +FUNC_MAX=126 +FUNC_MIN=127 +FUNC_DET=128 +FUNC_EYE_NAME=129 +FUNC_ZEROS_NAME=130 +FUNC_ONES_NAME=131 +FUNC_COLS_NAME=132 +FUNC_ROWS_NAME=133 +FUNC_DIAG_NAME=134 +FUNC_NORM_NAME=135 +FUNC_RANK_NAME=136 +FUNC_TRACE_NAME=137 +FUNC_RREF_NAME=138 +FUNC_HSTACK_NAME=139 +FUNC_VSTACK_NAME=140 +FUNC_ORTHOGONALIZE_NAME=141 +FUNC_NULLSPACE_NAME=142 +FUNC_DIAGONALIZE_NAME=143 +FUNC_EIGENVALS_NAME=144 +FUNC_EIGENVECTORS_NAME=145 +FUNC_SVD_NAME=146 +CMD_TIMES=147 +CMD_CDOT=148 +CMD_DIV=149 +CMD_FRAC=150 +CMD_BINOM=151 +CMD_CHOOSE=152 +CMD_MOD=153 +CMD_MATHIT=154 +CMD_OPERATORNAME=155 +MATRIX_TYPE_MATRIX=156 +MATRIX_TYPE_PMATRIX=157 +MATRIX_TYPE_BMATRIX=158 +MATRIX_TYPE_DET=159 +MATRIX_TYPES=160 +CMD_MATRIX_START=161 +CMD_MATRIX_END=162 +CMD_DET_START=163 +CMD_DET_END=164 +MATRIX_DEL_COL=165 +MATRIX_DEL_ROW=166 +UNDERSCORE=167 +CARET=168 +COLON=169 +SEMICOLON=170 +COMMA=171 +PERIOD=172 +DIFFERENTIAL=173 +EXP_E=174 +E_NOTATION_E=175 +LETTER_NO_E=176 +MATRIX_XRIGHTARROW=177 +TRANSFORM_EXCHANGE=178 +NUMBER=179 +E_NOTATION=180 +IN=181 +ASSIGNMENT=182 +EQUAL=183 +LT=184 +LTE=185 +GT=186 +GTE=187 +UNEQUAL=188 +BANG=189 +PERCENT_NUMBER=190 +GREEK_CMD=191 +OTHER_SYMBOL_CMD=192 +SYMBOL=193 +VARIABLE=194 +'\\acute'=1 +'\\bar'=2 +'\\overline'=3 +'\\breve'=4 +'\\check'=5 +'\\widecheck'=6 +'\\dot'=7 +'\\ddot'=8 +'\\grave'=9 +'\\hat'=10 +'\\tilde'=11 +'\\widetilde'=12 +'\\vec'=13 +'\\overrightarrow'=14 +'\\bm'=15 +'\\boldsymbol'=16 +'\\text'=17 +'\\textit'=18 +'\\mathbb'=19 +'\\mathbin'=20 +'\\mathbf'=21 +'\\mathcal'=22 +'\\mathclap'=23 +'\\mathclose'=24 +'\\mathellipsis'=25 +'\\mathfrak'=26 +'\\mathinner'=27 +'\\mathnormal'=28 +'\\mathop'=29 +'\\mathopen'=30 +'\\mathord'=31 +'\\mathpunct'=32 +'\\mathrel'=33 +'\\mathring'=34 +'\\mathrlap'=35 +'\\mathrm'=36 +'\\mathscr'=37 +'\\mathsf'=38 +'\\mathsterling'=39 +'\\mathtt'=40 +'^T'=41 +'^{T}'=42 +'^{\\top}'=43 +'\''=44 +'\\$'=46 +'+'=47 +'-'=48 +'*'=49 +'('=51 +')'=52 +'\\lgroup'=53 +'\\rgroup'=54 +'{'=55 +'}'=56 +'\\{'=57 +'\\}'=58 +'\\lbrace'=59 +'\\rbrace'=60 +'['=61 +']'=62 +'\\lbrack'=63 +'\\rbrack'=64 +'|'=65 +'\\lvert'=66 +'\\rvert'=67 +'\\vert'=68 +'\\|'=69 +'\\lfloor'=70 +'\\rfloor'=71 +'\\llcorner'=72 +'\\lrcorner'=73 +'\\lceil'=74 +'\\rceil'=75 +'\\ulcorner'=76 +'\\urcorner'=77 +'\\left'=78 +'\\right'=79 +'\\mleft'=80 +'\\mright'=81 +'\\lim'=82 +'\\int'=84 +'\\sum'=85 +'\\prod'=86 +'\\log'=87 +'\\ln'=88 +'\\exp'=89 +'\\sin'=90 +'\\cos'=91 +'\\tan'=92 +'\\csc'=93 +'\\sec'=94 +'\\cot'=95 +'\\arcsin'=96 +'\\arccos'=97 +'\\arctan'=98 +'\\arccsc'=99 +'\\arcsec'=100 +'\\arccot'=101 +'\\sinh'=102 +'\\cosh'=103 +'\\tanh'=104 +'\\arsinh'=105 +'\\arcosh'=106 +'\\artanh'=107 +'\\arcsinh'=108 +'\\arccosh'=109 +'\\arctanh'=110 +'arsinh'=111 +'arcsinh'=112 +'arcosh'=113 +'arccosh'=114 +'artanh'=115 +'arctanh'=116 +'gcd'=117 +'lcm'=118 +'floor'=119 +'ceil'=120 +'\\sqrt'=121 +'\\gcd'=122 +'\\lcm'=123 +'\\floor'=124 +'\\ceil'=125 +'\\max'=126 +'\\min'=127 +'\\det'=128 +'eye'=129 +'zeros'=130 +'ones'=131 +'cols'=132 +'rows'=133 +'diag'=134 +'norm'=135 +'rank'=136 +'rref'=138 +'hstack'=139 +'vstack'=140 +'nullspace'=142 +'\\times'=147 +'\\cdot'=148 +'\\div'=149 +'\\frac'=150 +'\\choose'=152 +'\\mod'=153 +'\\mathit'=154 +'\\operatorname'=155 +'matrix'=156 +'pmatrix'=157 +'bmatrix'=158 +'vmatrix'=159 +'&'=165 +'\\\\'=166 +'_'=167 +'^'=168 +':'=169 +';'=170 +','=171 +'.'=172 +'E'=175 +'\\in'=181 +'='=182 +'<'=184 +'>'=186 +'!'=189 diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.interp b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.interp new file mode 100755 index 0000000..675645c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.interp @@ -0,0 +1,612 @@ +token literal names: +null +'\\acute' +'\\bar' +'\\overline' +'\\breve' +'\\check' +'\\widecheck' +'\\dot' +'\\ddot' +'\\grave' +'\\hat' +'\\tilde' +'\\widetilde' +'\\vec' +'\\overrightarrow' +'\\bm' +'\\boldsymbol' +'\\text' +'\\textit' +'\\mathbb' +'\\mathbin' +'\\mathbf' +'\\mathcal' +'\\mathclap' +'\\mathclose' +'\\mathellipsis' +'\\mathfrak' +'\\mathinner' +'\\mathnormal' +'\\mathop' +'\\mathopen' +'\\mathord' +'\\mathpunct' +'\\mathrel' +'\\mathring' +'\\mathrlap' +'\\mathrm' +'\\mathscr' +'\\mathsf' +'\\mathsterling' +'\\mathtt' +'^T' +'^{T}' +'^{\\top}' +'\'' +null +'\\$' +'+' +'-' +'*' +null +'(' +')' +'\\lgroup' +'\\rgroup' +'{' +'}' +'\\{' +'\\}' +'\\lbrace' +'\\rbrace' +'[' +']' +'\\lbrack' +'\\rbrack' +'|' +'\\lvert' +'\\rvert' +'\\vert' +'\\|' +'\\lfloor' +'\\rfloor' +'\\llcorner' +'\\lrcorner' +'\\lceil' +'\\rceil' +'\\ulcorner' +'\\urcorner' +'\\left' +'\\right' +'\\mleft' +'\\mright' +'\\lim' +null +'\\int' +'\\sum' +'\\prod' +'\\log' +'\\ln' +'\\exp' +'\\sin' +'\\cos' +'\\tan' +'\\csc' +'\\sec' +'\\cot' +'\\arcsin' +'\\arccos' +'\\arctan' +'\\arccsc' +'\\arcsec' +'\\arccot' +'\\sinh' +'\\cosh' +'\\tanh' +'\\arsinh' +'\\arcosh' +'\\artanh' +'\\arcsinh' +'\\arccosh' +'\\arctanh' +'arsinh' +'arcsinh' +'arcosh' +'arccosh' +'artanh' +'arctanh' +'gcd' +'lcm' +'floor' +'ceil' +'\\sqrt' +'\\gcd' +'\\lcm' +'\\floor' +'\\ceil' +'\\max' +'\\min' +'\\det' +'eye' +'zeros' +'ones' +'cols' +'rows' +'diag' +'norm' +'rank' +null +'rref' +'hstack' +'vstack' +null +'nullspace' +null +null +null +null +'\\times' +'\\cdot' +'\\div' +'\\frac' +null +'\\choose' +'\\mod' +'\\mathit' +'\\operatorname' +'matrix' +'pmatrix' +'bmatrix' +'vmatrix' +null +null +null +null +null +'&' +'\\\\' +'_' +'^' +':' +';' +',' +'.' +null +null +'E' +null +null +null +null +null +'\\in' +'=' +null +'<' +null +'>' +null +null +'!' +null +null +null +null +null + +token symbolic names: +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +null +WS +DOLLAR_SIGN +ADD +SUB +MUL +DIV +L_PAREN +R_PAREN +L_GROUP +R_GROUP +L_BRACE +R_BRACE +L_BRACE_VISUAL +R_BRACE_VISUAL +L_BRACE_CMD +R_BRACE_CMD +L_BRACKET +R_BRACKET +L_BRACK +R_BRACK +BAR +L_VERT +R_VERT +VERT +NORM +L_FLOOR +R_FLOOR +LL_CORNER +LR_CORNER +L_CEIL +R_CEIL +UL_CORNER +UR_CORNER +L_LEFT +R_RIGHT +ML_LEFT +MR_RIGHT +FUNC_LIM +LIM_APPROACH_SYM +FUNC_INT +FUNC_SUM +FUNC_PROD +FUNC_LOG +FUNC_LN +FUNC_EXP +FUNC_SIN +FUNC_COS +FUNC_TAN +FUNC_CSC +FUNC_SEC +FUNC_COT +FUNC_ARCSIN +FUNC_ARCCOS +FUNC_ARCTAN +FUNC_ARCCSC +FUNC_ARCSEC +FUNC_ARCCOT +FUNC_SINH +FUNC_COSH +FUNC_TANH +FUNC_ARSINH +FUNC_ARCOSH +FUNC_ARTANH +FUNC_ARCSINH +FUNC_ARCCOSH +FUNC_ARCTANH +FUNC_ARSINH_NAME +FUNC_ARCSINH_NAME +FUNC_ARCOSH_NAME +FUNC_ARCCOSH_NAME +FUNC_ARTANH_NAME +FUNC_ARCTANH_NAME +FUNC_GCD_NAME +FUNC_LCM_NAME +FUNC_FLOOR_NAME +FUNC_CEIL_NAME +FUNC_SQRT +FUNC_GCD +FUNC_LCM +FUNC_FLOOR +FUNC_CEIL +FUNC_MAX +FUNC_MIN +FUNC_DET +FUNC_EYE_NAME +FUNC_ZEROS_NAME +FUNC_ONES_NAME +FUNC_COLS_NAME +FUNC_ROWS_NAME +FUNC_DIAG_NAME +FUNC_NORM_NAME +FUNC_RANK_NAME +FUNC_TRACE_NAME +FUNC_RREF_NAME +FUNC_HSTACK_NAME +FUNC_VSTACK_NAME +FUNC_ORTHOGONALIZE_NAME +FUNC_NULLSPACE_NAME +FUNC_DIAGONALIZE_NAME +FUNC_EIGENVALS_NAME +FUNC_EIGENVECTORS_NAME +FUNC_SVD_NAME +CMD_TIMES +CMD_CDOT +CMD_DIV +CMD_FRAC +CMD_BINOM +CMD_CHOOSE +CMD_MOD +CMD_MATHIT +CMD_OPERATORNAME +MATRIX_TYPE_MATRIX +MATRIX_TYPE_PMATRIX +MATRIX_TYPE_BMATRIX +MATRIX_TYPE_DET +MATRIX_TYPES +CMD_MATRIX_START +CMD_MATRIX_END +CMD_DET_START +CMD_DET_END +MATRIX_DEL_COL +MATRIX_DEL_ROW +UNDERSCORE +CARET +COLON +SEMICOLON +COMMA +PERIOD +DIFFERENTIAL +EXP_E +E_NOTATION_E +LETTER_NO_E +MATRIX_XRIGHTARROW +TRANSFORM_EXCHANGE +NUMBER +E_NOTATION +IN +ASSIGNMENT +EQUAL +LT +LTE +GT +GTE +UNEQUAL +BANG +PERCENT_NUMBER +GREEK_CMD +OTHER_SYMBOL_CMD +SYMBOL +VARIABLE + +rule names: +T__0 +T__1 +T__2 +T__3 +T__4 +T__5 +T__6 +T__7 +T__8 +T__9 +T__10 +T__11 +T__12 +T__13 +T__14 +T__15 +T__16 +T__17 +T__18 +T__19 +T__20 +T__21 +T__22 +T__23 +T__24 +T__25 +T__26 +T__27 +T__28 +T__29 +T__30 +T__31 +T__32 +T__33 +T__34 +T__35 +T__36 +T__37 +T__38 +T__39 +T__40 +T__41 +T__42 +T__43 +WS +DOLLAR_SIGN +ADD +SUB +MUL +DIV +L_PAREN +R_PAREN +L_GROUP +R_GROUP +L_BRACE +R_BRACE +L_BRACE_VISUAL +R_BRACE_VISUAL +L_BRACE_CMD +R_BRACE_CMD +L_BRACKET +R_BRACKET +L_BRACK +R_BRACK +BAR +L_VERT +R_VERT +VERT +NORM +L_FLOOR +R_FLOOR +LL_CORNER +LR_CORNER +L_CEIL +R_CEIL +UL_CORNER +UR_CORNER +L_LEFT +R_RIGHT +ML_LEFT +MR_RIGHT +FUNC_LIM +LIM_APPROACH_SYM +FUNC_INT +FUNC_SUM +FUNC_PROD +FUNC_LOG +FUNC_LN +FUNC_EXP +FUNC_SIN +FUNC_COS +FUNC_TAN +FUNC_CSC +FUNC_SEC +FUNC_COT +FUNC_ARCSIN +FUNC_ARCCOS +FUNC_ARCTAN +FUNC_ARCCSC +FUNC_ARCSEC +FUNC_ARCCOT +FUNC_SINH +FUNC_COSH +FUNC_TANH +FUNC_ARSINH +FUNC_ARCOSH +FUNC_ARTANH +FUNC_ARCSINH +FUNC_ARCCOSH +FUNC_ARCTANH +FUNC_ARSINH_NAME +FUNC_ARCSINH_NAME +FUNC_ARCOSH_NAME +FUNC_ARCCOSH_NAME +FUNC_ARTANH_NAME +FUNC_ARCTANH_NAME +FUNC_GCD_NAME +FUNC_LCM_NAME +FUNC_FLOOR_NAME +FUNC_CEIL_NAME +FUNC_SQRT +FUNC_GCD +FUNC_LCM +FUNC_FLOOR +FUNC_CEIL +FUNC_MAX +FUNC_MIN +FUNC_DET +FUNC_EYE_NAME +FUNC_ZEROS_NAME +FUNC_ONES_NAME +FUNC_COLS_NAME +FUNC_ROWS_NAME +FUNC_DIAG_NAME +FUNC_NORM_NAME +FUNC_RANK_NAME +FUNC_TRACE_NAME +FUNC_RREF_NAME +FUNC_HSTACK_NAME +FUNC_VSTACK_NAME +FUNC_ORTHOGONALIZE_NAME +FUNC_NULLSPACE_NAME +FUNC_DIAGONALIZE_NAME +FUNC_EIGENVALS_NAME +FUNC_EIGENVECTORS_NAME +FUNC_SVD_NAME +CMD_TIMES +CMD_CDOT +CMD_DIV +CMD_FRAC +CMD_BINOM +CMD_CHOOSE +CMD_MOD +CMD_MATHIT +CMD_OPERATORNAME +MATRIX_TYPE_MATRIX +MATRIX_TYPE_PMATRIX +MATRIX_TYPE_BMATRIX +MATRIX_TYPE_DET +MATRIX_TYPES +CMD_MATRIX_START +CMD_MATRIX_END +CMD_DET_START +CMD_DET_END +MATRIX_DEL_COL +MATRIX_DEL_ROW +UNDERSCORE +CARET +COLON +SEMICOLON +COMMA +PERIOD +WS_CHAR +DIFFERENTIAL +EXP_E +E_NOTATION_E +LETTER_NO_E +LETTER +DIGIT +MATRIX_XRIGHTARROW +TRANSFORM_EXCHANGE +NUMBER +E_NOTATION +IN +ASSIGNMENT +EQUAL +LT +LTE +GT +GTE +UNEQUAL +BANG +PERCENT_SIGN +PERCENT_NUMBER +GREEK_LETTER +GREEK_CMD +OTHER_SYMBOL +OTHER_SYMBOL_CMD +PI +INFTY_CMD +PARTIAL_CMD +INFTY +EMPTYSET +SYMBOL +VARIABLE_CMD +VARIABLE_SYMBOL +VARIABLE + +channel names: +DEFAULT_TOKEN_CHANNEL +HIDDEN + +mode names: +DEFAULT_MODE + +atn: +[4, 0, 194, 2795, 6, -1, 2, 0, 7, 0, 2, 1, 7, 1, 2, 2, 7, 2, 2, 3, 7, 3, 2, 4, 7, 4, 2, 5, 7, 5, 2, 6, 7, 6, 2, 7, 7, 7, 2, 8, 7, 8, 2, 9, 7, 9, 2, 10, 7, 10, 2, 11, 7, 11, 2, 12, 7, 12, 2, 13, 7, 13, 2, 14, 7, 14, 2, 15, 7, 15, 2, 16, 7, 16, 2, 17, 7, 17, 2, 18, 7, 18, 2, 19, 7, 19, 2, 20, 7, 20, 2, 21, 7, 21, 2, 22, 7, 22, 2, 23, 7, 23, 2, 24, 7, 24, 2, 25, 7, 25, 2, 26, 7, 26, 2, 27, 7, 27, 2, 28, 7, 28, 2, 29, 7, 29, 2, 30, 7, 30, 2, 31, 7, 31, 2, 32, 7, 32, 2, 33, 7, 33, 2, 34, 7, 34, 2, 35, 7, 35, 2, 36, 7, 36, 2, 37, 7, 37, 2, 38, 7, 38, 2, 39, 7, 39, 2, 40, 7, 40, 2, 41, 7, 41, 2, 42, 7, 42, 2, 43, 7, 43, 2, 44, 7, 44, 2, 45, 7, 45, 2, 46, 7, 46, 2, 47, 7, 47, 2, 48, 7, 48, 2, 49, 7, 49, 2, 50, 7, 50, 2, 51, 7, 51, 2, 52, 7, 52, 2, 53, 7, 53, 2, 54, 7, 54, 2, 55, 7, 55, 2, 56, 7, 56, 2, 57, 7, 57, 2, 58, 7, 58, 2, 59, 7, 59, 2, 60, 7, 60, 2, 61, 7, 61, 2, 62, 7, 62, 2, 63, 7, 63, 2, 64, 7, 64, 2, 65, 7, 65, 2, 66, 7, 66, 2, 67, 7, 67, 2, 68, 7, 68, 2, 69, 7, 69, 2, 70, 7, 70, 2, 71, 7, 71, 2, 72, 7, 72, 2, 73, 7, 73, 2, 74, 7, 74, 2, 75, 7, 75, 2, 76, 7, 76, 2, 77, 7, 77, 2, 78, 7, 78, 2, 79, 7, 79, 2, 80, 7, 80, 2, 81, 7, 81, 2, 82, 7, 82, 2, 83, 7, 83, 2, 84, 7, 84, 2, 85, 7, 85, 2, 86, 7, 86, 2, 87, 7, 87, 2, 88, 7, 88, 2, 89, 7, 89, 2, 90, 7, 90, 2, 91, 7, 91, 2, 92, 7, 92, 2, 93, 7, 93, 2, 94, 7, 94, 2, 95, 7, 95, 2, 96, 7, 96, 2, 97, 7, 97, 2, 98, 7, 98, 2, 99, 7, 99, 2, 100, 7, 100, 2, 101, 7, 101, 2, 102, 7, 102, 2, 103, 7, 103, 2, 104, 7, 104, 2, 105, 7, 105, 2, 106, 7, 106, 2, 107, 7, 107, 2, 108, 7, 108, 2, 109, 7, 109, 2, 110, 7, 110, 2, 111, 7, 111, 2, 112, 7, 112, 2, 113, 7, 113, 2, 114, 7, 114, 2, 115, 7, 115, 2, 116, 7, 116, 2, 117, 7, 117, 2, 118, 7, 118, 2, 119, 7, 119, 2, 120, 7, 120, 2, 121, 7, 121, 2, 122, 7, 122, 2, 123, 7, 123, 2, 124, 7, 124, 2, 125, 7, 125, 2, 126, 7, 126, 2, 127, 7, 127, 2, 128, 7, 128, 2, 129, 7, 129, 2, 130, 7, 130, 2, 131, 7, 131, 2, 132, 7, 132, 2, 133, 7, 133, 2, 134, 7, 134, 2, 135, 7, 135, 2, 136, 7, 136, 2, 137, 7, 137, 2, 138, 7, 138, 2, 139, 7, 139, 2, 140, 7, 140, 2, 141, 7, 141, 2, 142, 7, 142, 2, 143, 7, 143, 2, 144, 7, 144, 2, 145, 7, 145, 2, 146, 7, 146, 2, 147, 7, 147, 2, 148, 7, 148, 2, 149, 7, 149, 2, 150, 7, 150, 2, 151, 7, 151, 2, 152, 7, 152, 2, 153, 7, 153, 2, 154, 7, 154, 2, 155, 7, 155, 2, 156, 7, 156, 2, 157, 7, 157, 2, 158, 7, 158, 2, 159, 7, 159, 2, 160, 7, 160, 2, 161, 7, 161, 2, 162, 7, 162, 2, 163, 7, 163, 2, 164, 7, 164, 2, 165, 7, 165, 2, 166, 7, 166, 2, 167, 7, 167, 2, 168, 7, 168, 2, 169, 7, 169, 2, 170, 7, 170, 2, 171, 7, 171, 2, 172, 7, 172, 2, 173, 7, 173, 2, 174, 7, 174, 2, 175, 7, 175, 2, 176, 7, 176, 2, 177, 7, 177, 2, 178, 7, 178, 2, 179, 7, 179, 2, 180, 7, 180, 2, 181, 7, 181, 2, 182, 7, 182, 2, 183, 7, 183, 2, 184, 7, 184, 2, 185, 7, 185, 2, 186, 7, 186, 2, 187, 7, 187, 2, 188, 7, 188, 2, 189, 7, 189, 2, 190, 7, 190, 2, 191, 7, 191, 2, 192, 7, 192, 2, 193, 7, 193, 2, 194, 7, 194, 2, 195, 7, 195, 2, 196, 7, 196, 2, 197, 7, 197, 2, 198, 7, 198, 2, 199, 7, 199, 2, 200, 7, 200, 2, 201, 7, 201, 2, 202, 7, 202, 2, 203, 7, 203, 2, 204, 7, 204, 2, 205, 7, 205, 2, 206, 7, 206, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 4, 1, 4, 1, 4, 1, 4, 1, 4, 1, 4, 1, 4, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 6, 1, 6, 1, 6, 1, 6, 1, 6, 1, 7, 1, 7, 1, 7, 1, 7, 1, 7, 1, 7, 1, 8, 1, 8, 1, 8, 1, 8, 1, 8, 1, 8, 1, 8, 1, 9, 1, 9, 1, 9, 1, 9, 1, 9, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 12, 1, 12, 1, 12, 1, 12, 1, 12, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 14, 1, 14, 1, 14, 1, 14, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 16, 1, 16, 1, 16, 1, 16, 1, 16, 1, 16, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 20, 1, 20, 1, 20, 1, 20, 1, 20, 1, 20, 1, 20, 1, 20, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 40, 1, 40, 1, 40, 1, 41, 1, 41, 1, 41, 1, 41, 1, 41, 1, 42, 1, 42, 1, 42, 1, 42, 1, 42, 1, 42, 1, 42, 1, 42, 1, 43, 1, 43, 1, 44, 4, 44, 790, 8, 44, 11, 44, 12, 44, 791, 1, 44, 1, 44, 1, 45, 1, 45, 1, 45, 1, 45, 1, 45, 1, 46, 1, 46, 1, 47, 1, 47, 1, 48, 1, 48, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 3, 49, 813, 8, 49, 1, 50, 1, 50, 1, 51, 1, 51, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 54, 1, 54, 1, 55, 1, 55, 1, 56, 1, 56, 1, 56, 1, 57, 1, 57, 1, 57, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 59, 1, 59, 1, 59, 1, 59, 1, 59, 1, 59, 1, 59, 1, 59, 1, 60, 1, 60, 1, 61, 1, 61, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 64, 1, 64, 1, 65, 1, 65, 1, 65, 1, 65, 1, 65, 1, 65, 1, 65, 1, 66, 1, 66, 1, 66, 1, 66, 1, 66, 1, 66, 1, 66, 1, 67, 1, 67, 1, 67, 1, 67, 1, 67, 1, 67, 1, 68, 1, 68, 1, 68, 1, 69, 1, 69, 1, 69, 1, 69, 1, 69, 1, 69, 1, 69, 1, 69, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 73, 1, 73, 1, 73, 1, 73, 1, 73, 1, 73, 1, 73, 1, 74, 1, 74, 1, 74, 1, 74, 1, 74, 1, 74, 1, 74, 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 77, 1, 77, 1, 77, 1, 77, 1, 77, 1, 77, 1, 78, 1, 78, 1, 78, 1, 78, 1, 78, 1, 78, 1, 78, 1, 79, 1, 79, 1, 79, 1, 79, 1, 79, 1, 79, 1, 79, 1, 80, 1, 80, 1, 80, 1, 80, 1, 80, 1, 80, 1, 80, 1, 80, 1, 81, 1, 81, 1, 81, 1, 81, 1, 81, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 3, 82, 1064, 8, 82, 1, 83, 1, 83, 1, 83, 1, 83, 1, 83, 1, 84, 1, 84, 1, 84, 1, 84, 1, 84, 1, 85, 1, 85, 1, 85, 1, 85, 1, 85, 1, 85, 1, 86, 1, 86, 1, 86, 1, 86, 1, 86, 1, 87, 1, 87, 1, 87, 1, 87, 1, 88, 1, 88, 1, 88, 1, 88, 1, 88, 1, 89, 1, 89, 1, 89, 1, 89, 1, 89, 1, 90, 1, 90, 1, 90, 1, 90, 1, 90, 1, 91, 1, 91, 1, 91, 1, 91, 1, 91, 1, 92, 1, 92, 1, 92, 1, 92, 1, 92, 1, 93, 1, 93, 1, 93, 1, 93, 1, 93, 1, 94, 1, 94, 1, 94, 1, 94, 1, 94, 1, 95, 1, 95, 1, 95, 1, 95, 1, 95, 1, 95, 1, 95, 1, 95, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 98, 1, 98, 1, 98, 1, 98, 1, 98, 1, 98, 1, 98, 1, 98, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 100, 1, 100, 1, 100, 1, 100, 1, 100, 1, 100, 1, 100, 1, 100, 1, 101, 1, 101, 1, 101, 1, 101, 1, 101, 1, 101, 1, 102, 1, 102, 1, 102, 1, 102, 1, 102, 1, 102, 1, 103, 1, 103, 1, 103, 1, 103, 1, 103, 1, 103, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 105, 1, 105, 1, 105, 1, 105, 1, 105, 1, 105, 1, 105, 1, 105, 1, 106, 1, 106, 1, 106, 1, 106, 1, 106, 1, 106, 1, 106, 1, 106, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 110, 1, 110, 1, 110, 1, 110, 1, 110, 1, 110, 1, 110, 1, 111, 1, 111, 1, 111, 1, 111, 1, 111, 1, 111, 1, 111, 1, 111, 1, 112, 1, 112, 1, 112, 1, 112, 1, 112, 1, 112, 1, 112, 1, 113, 1, 113, 1, 113, 1, 113, 1, 113, 1, 113, 1, 113, 1, 113, 1, 114, 1, 114, 1, 114, 1, 114, 1, 114, 1, 114, 1, 114, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 116, 1, 116, 1, 116, 1, 116, 1, 117, 1, 117, 1, 117, 1, 117, 1, 118, 1, 118, 1, 118, 1, 118, 1, 118, 1, 118, 1, 119, 1, 119, 1, 119, 1, 119, 1, 119, 1, 120, 1, 120, 1, 120, 1, 120, 1, 120, 1, 120, 1, 121, 1, 121, 1, 121, 1, 121, 1, 121, 1, 122, 1, 122, 1, 122, 1, 122, 1, 122, 1, 123, 1, 123, 1, 123, 1, 123, 1, 123, 1, 123, 1, 123, 1, 124, 1, 124, 1, 124, 1, 124, 1, 124, 1, 124, 1, 125, 1, 125, 1, 125, 1, 125, 1, 125, 1, 126, 1, 126, 1, 126, 1, 126, 1, 126, 1, 127, 1, 127, 1, 127, 1, 127, 1, 127, 1, 128, 1, 128, 1, 128, 1, 128, 1, 129, 1, 129, 1, 129, 1, 129, 1, 129, 1, 129, 1, 130, 1, 130, 1, 130, 1, 130, 1, 130, 1, 131, 1, 131, 1, 131, 1, 131, 1, 131, 1, 132, 1, 132, 1, 132, 1, 132, 1, 132, 1, 133, 1, 133, 1, 133, 1, 133, 1, 133, 1, 134, 1, 134, 1, 134, 1, 134, 1, 134, 1, 135, 1, 135, 1, 135, 1, 135, 1, 135, 1, 136, 1, 136, 1, 136, 1, 136, 1, 136, 1, 136, 1, 136, 3, 136, 1398, 8, 136, 1, 137, 1, 137, 1, 137, 1, 137, 1, 137, 1, 138, 1, 138, 1, 138, 1, 138, 1, 138, 1, 138, 1, 138, 1, 139, 1, 139, 1, 139, 1, 139, 1, 139, 1, 139, 1, 139, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 3, 140, 1451, 8, 140, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 3, 142, 1482, 8, 142, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 3, 143, 1504, 8, 143, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 3, 144, 1528, 8, 144, 1, 145, 1, 145, 1, 145, 1, 145, 1, 145, 1, 145, 3, 145, 1536, 8, 145, 1, 146, 1, 146, 1, 146, 1, 146, 1, 146, 1, 146, 1, 146, 1, 147, 1, 147, 1, 147, 1, 147, 1, 147, 1, 147, 1, 148, 1, 148, 1, 148, 1, 148, 1, 148, 1, 149, 1, 149, 1, 149, 1, 149, 1, 149, 1, 149, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 3, 150, 1582, 8, 150, 1, 151, 1, 151, 1, 151, 1, 151, 1, 151, 1, 151, 1, 151, 1, 151, 1, 152, 1, 152, 1, 152, 1, 152, 1, 152, 1, 153, 1, 153, 1, 153, 1, 153, 1, 153, 1, 153, 1, 153, 1, 153, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 155, 1, 155, 1, 155, 1, 155, 1, 155, 1, 155, 1, 155, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 158, 1, 158, 1, 158, 1, 158, 1, 158, 1, 158, 1, 158, 1, 158, 1, 159, 1, 159, 1, 159, 3, 159, 1653, 8, 159, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 164, 1, 164, 1, 165, 1, 165, 1, 165, 1, 166, 1, 166, 1, 167, 1, 167, 1, 168, 1, 168, 1, 169, 1, 169, 1, 170, 1, 170, 1, 171, 1, 171, 1, 172, 1, 172, 1, 173, 1, 173, 5, 173, 1716, 8, 173, 10, 173, 12, 173, 1719, 9, 173, 1, 173, 1, 173, 1, 173, 4, 173, 1724, 8, 173, 11, 173, 12, 173, 1725, 3, 173, 1728, 8, 173, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 3, 174, 1744, 8, 174, 1, 175, 1, 175, 1, 176, 1, 176, 1, 177, 1, 177, 1, 178, 1, 178, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 3, 179, 1778, 8, 179, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 3, 180, 1816, 8, 180, 1, 181, 4, 181, 1819, 8, 181, 11, 181, 12, 181, 1820, 1, 181, 1, 181, 1, 181, 1, 181, 1, 181, 5, 181, 1828, 8, 181, 10, 181, 12, 181, 1831, 9, 181, 1, 181, 5, 181, 1834, 8, 181, 10, 181, 12, 181, 1837, 9, 181, 1, 181, 1, 181, 1, 181, 1, 181, 1, 181, 5, 181, 1844, 8, 181, 10, 181, 12, 181, 1847, 9, 181, 1, 181, 1, 181, 4, 181, 1851, 8, 181, 11, 181, 12, 181, 1852, 3, 181, 1855, 8, 181, 1, 182, 1, 182, 1, 182, 1, 182, 3, 182, 1861, 8, 182, 1, 182, 4, 182, 1864, 8, 182, 11, 182, 12, 182, 1865, 1, 183, 1, 183, 1, 183, 1, 183, 1, 184, 1, 184, 1, 185, 1, 185, 1, 185, 1, 185, 1, 185, 1, 185, 1, 185, 1, 185, 3, 185, 1882, 8, 185, 1, 186, 1, 186, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 3, 187, 1902, 8, 187, 1, 188, 1, 188, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 3, 189, 1922, 8, 189, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 3, 190, 1946, 8, 190, 1, 191, 1, 191, 1, 192, 1, 192, 1, 192, 1, 193, 1, 193, 1, 193, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 3, 194, 2341, 8, 194, 1, 195, 1, 195, 3, 195, 2345, 8, 195, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 3, 196, 2697, 8, 196, 1, 197, 1, 197, 3, 197, 2701, 8, 197, 1, 198, 1, 198, 1, 198, 1, 198, 1, 199, 1, 199, 1, 199, 1, 199, 1, 199, 1, 199, 1, 199, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 201, 1, 201, 1, 201, 1, 201, 1, 201, 1, 201, 1, 201, 3, 201, 2730, 8, 201, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 203, 1, 203, 1, 203, 1, 203, 3, 203, 2746, 8, 203, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 205, 1, 205, 1, 205, 1, 205, 4, 205, 2762, 8, 205, 11, 205, 12, 205, 2763, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 4, 205, 2773, 8, 205, 11, 205, 12, 205, 2774, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 3, 205, 2783, 8, 205, 3, 205, 2785, 8, 205, 3, 205, 2787, 8, 205, 1, 206, 1, 206, 1, 206, 1, 206, 1, 206, 3, 206, 2794, 8, 206, 1, 1717, 0, 207, 1, 1, 3, 2, 5, 3, 7, 4, 9, 5, 11, 6, 13, 7, 15, 8, 17, 9, 19, 10, 21, 11, 23, 12, 25, 13, 27, 14, 29, 15, 31, 16, 33, 17, 35, 18, 37, 19, 39, 20, 41, 21, 43, 22, 45, 23, 47, 24, 49, 25, 51, 26, 53, 27, 55, 28, 57, 29, 59, 30, 61, 31, 63, 32, 65, 33, 67, 34, 69, 35, 71, 36, 73, 37, 75, 38, 77, 39, 79, 40, 81, 41, 83, 42, 85, 43, 87, 44, 89, 45, 91, 46, 93, 47, 95, 48, 97, 49, 99, 50, 101, 51, 103, 52, 105, 53, 107, 54, 109, 55, 111, 56, 113, 57, 115, 58, 117, 59, 119, 60, 121, 61, 123, 62, 125, 63, 127, 64, 129, 65, 131, 66, 133, 67, 135, 68, 137, 69, 139, 70, 141, 71, 143, 72, 145, 73, 147, 74, 149, 75, 151, 76, 153, 77, 155, 78, 157, 79, 159, 80, 161, 81, 163, 82, 165, 83, 167, 84, 169, 85, 171, 86, 173, 87, 175, 88, 177, 89, 179, 90, 181, 91, 183, 92, 185, 93, 187, 94, 189, 95, 191, 96, 193, 97, 195, 98, 197, 99, 199, 100, 201, 101, 203, 102, 205, 103, 207, 104, 209, 105, 211, 106, 213, 107, 215, 108, 217, 109, 219, 110, 221, 111, 223, 112, 225, 113, 227, 114, 229, 115, 231, 116, 233, 117, 235, 118, 237, 119, 239, 120, 241, 121, 243, 122, 245, 123, 247, 124, 249, 125, 251, 126, 253, 127, 255, 128, 257, 129, 259, 130, 261, 131, 263, 132, 265, 133, 267, 134, 269, 135, 271, 136, 273, 137, 275, 138, 277, 139, 279, 140, 281, 141, 283, 142, 285, 143, 287, 144, 289, 145, 291, 146, 293, 147, 295, 148, 297, 149, 299, 150, 301, 151, 303, 152, 305, 153, 307, 154, 309, 155, 311, 156, 313, 157, 315, 158, 317, 159, 319, 160, 321, 161, 323, 162, 325, 163, 327, 164, 329, 165, 331, 166, 333, 167, 335, 168, 337, 169, 339, 170, 341, 171, 343, 172, 345, 0, 347, 173, 349, 174, 351, 175, 353, 176, 355, 0, 357, 0, 359, 177, 361, 178, 363, 179, 365, 180, 367, 181, 369, 182, 371, 183, 373, 184, 375, 185, 377, 186, 379, 187, 381, 188, 383, 189, 385, 0, 387, 190, 389, 0, 391, 191, 393, 0, 395, 192, 397, 0, 399, 0, 401, 0, 403, 0, 405, 0, 407, 193, 409, 0, 411, 0, 413, 194, 1, 0, 5, 3, 0, 9, 10, 13, 13, 32, 32, 2, 0, 65, 90, 97, 122, 4, 0, 65, 68, 70, 90, 97, 100, 102, 122, 1, 0, 48, 57, 1, 0, 32, 32, 2943, 0, 1, 1, 0, 0, 0, 0, 3, 1, 0, 0, 0, 0, 5, 1, 0, 0, 0, 0, 7, 1, 0, 0, 0, 0, 9, 1, 0, 0, 0, 0, 11, 1, 0, 0, 0, 0, 13, 1, 0, 0, 0, 0, 15, 1, 0, 0, 0, 0, 17, 1, 0, 0, 0, 0, 19, 1, 0, 0, 0, 0, 21, 1, 0, 0, 0, 0, 23, 1, 0, 0, 0, 0, 25, 1, 0, 0, 0, 0, 27, 1, 0, 0, 0, 0, 29, 1, 0, 0, 0, 0, 31, 1, 0, 0, 0, 0, 33, 1, 0, 0, 0, 0, 35, 1, 0, 0, 0, 0, 37, 1, 0, 0, 0, 0, 39, 1, 0, 0, 0, 0, 41, 1, 0, 0, 0, 0, 43, 1, 0, 0, 0, 0, 45, 1, 0, 0, 0, 0, 47, 1, 0, 0, 0, 0, 49, 1, 0, 0, 0, 0, 51, 1, 0, 0, 0, 0, 53, 1, 0, 0, 0, 0, 55, 1, 0, 0, 0, 0, 57, 1, 0, 0, 0, 0, 59, 1, 0, 0, 0, 0, 61, 1, 0, 0, 0, 0, 63, 1, 0, 0, 0, 0, 65, 1, 0, 0, 0, 0, 67, 1, 0, 0, 0, 0, 69, 1, 0, 0, 0, 0, 71, 1, 0, 0, 0, 0, 73, 1, 0, 0, 0, 0, 75, 1, 0, 0, 0, 0, 77, 1, 0, 0, 0, 0, 79, 1, 0, 0, 0, 0, 81, 1, 0, 0, 0, 0, 83, 1, 0, 0, 0, 0, 85, 1, 0, 0, 0, 0, 87, 1, 0, 0, 0, 0, 89, 1, 0, 0, 0, 0, 91, 1, 0, 0, 0, 0, 93, 1, 0, 0, 0, 0, 95, 1, 0, 0, 0, 0, 97, 1, 0, 0, 0, 0, 99, 1, 0, 0, 0, 0, 101, 1, 0, 0, 0, 0, 103, 1, 0, 0, 0, 0, 105, 1, 0, 0, 0, 0, 107, 1, 0, 0, 0, 0, 109, 1, 0, 0, 0, 0, 111, 1, 0, 0, 0, 0, 113, 1, 0, 0, 0, 0, 115, 1, 0, 0, 0, 0, 117, 1, 0, 0, 0, 0, 119, 1, 0, 0, 0, 0, 121, 1, 0, 0, 0, 0, 123, 1, 0, 0, 0, 0, 125, 1, 0, 0, 0, 0, 127, 1, 0, 0, 0, 0, 129, 1, 0, 0, 0, 0, 131, 1, 0, 0, 0, 0, 133, 1, 0, 0, 0, 0, 135, 1, 0, 0, 0, 0, 137, 1, 0, 0, 0, 0, 139, 1, 0, 0, 0, 0, 141, 1, 0, 0, 0, 0, 143, 1, 0, 0, 0, 0, 145, 1, 0, 0, 0, 0, 147, 1, 0, 0, 0, 0, 149, 1, 0, 0, 0, 0, 151, 1, 0, 0, 0, 0, 153, 1, 0, 0, 0, 0, 155, 1, 0, 0, 0, 0, 157, 1, 0, 0, 0, 0, 159, 1, 0, 0, 0, 0, 161, 1, 0, 0, 0, 0, 163, 1, 0, 0, 0, 0, 165, 1, 0, 0, 0, 0, 167, 1, 0, 0, 0, 0, 169, 1, 0, 0, 0, 0, 171, 1, 0, 0, 0, 0, 173, 1, 0, 0, 0, 0, 175, 1, 0, 0, 0, 0, 177, 1, 0, 0, 0, 0, 179, 1, 0, 0, 0, 0, 181, 1, 0, 0, 0, 0, 183, 1, 0, 0, 0, 0, 185, 1, 0, 0, 0, 0, 187, 1, 0, 0, 0, 0, 189, 1, 0, 0, 0, 0, 191, 1, 0, 0, 0, 0, 193, 1, 0, 0, 0, 0, 195, 1, 0, 0, 0, 0, 197, 1, 0, 0, 0, 0, 199, 1, 0, 0, 0, 0, 201, 1, 0, 0, 0, 0, 203, 1, 0, 0, 0, 0, 205, 1, 0, 0, 0, 0, 207, 1, 0, 0, 0, 0, 209, 1, 0, 0, 0, 0, 211, 1, 0, 0, 0, 0, 213, 1, 0, 0, 0, 0, 215, 1, 0, 0, 0, 0, 217, 1, 0, 0, 0, 0, 219, 1, 0, 0, 0, 0, 221, 1, 0, 0, 0, 0, 223, 1, 0, 0, 0, 0, 225, 1, 0, 0, 0, 0, 227, 1, 0, 0, 0, 0, 229, 1, 0, 0, 0, 0, 231, 1, 0, 0, 0, 0, 233, 1, 0, 0, 0, 0, 235, 1, 0, 0, 0, 0, 237, 1, 0, 0, 0, 0, 239, 1, 0, 0, 0, 0, 241, 1, 0, 0, 0, 0, 243, 1, 0, 0, 0, 0, 245, 1, 0, 0, 0, 0, 247, 1, 0, 0, 0, 0, 249, 1, 0, 0, 0, 0, 251, 1, 0, 0, 0, 0, 253, 1, 0, 0, 0, 0, 255, 1, 0, 0, 0, 0, 257, 1, 0, 0, 0, 0, 259, 1, 0, 0, 0, 0, 261, 1, 0, 0, 0, 0, 263, 1, 0, 0, 0, 0, 265, 1, 0, 0, 0, 0, 267, 1, 0, 0, 0, 0, 269, 1, 0, 0, 0, 0, 271, 1, 0, 0, 0, 0, 273, 1, 0, 0, 0, 0, 275, 1, 0, 0, 0, 0, 277, 1, 0, 0, 0, 0, 279, 1, 0, 0, 0, 0, 281, 1, 0, 0, 0, 0, 283, 1, 0, 0, 0, 0, 285, 1, 0, 0, 0, 0, 287, 1, 0, 0, 0, 0, 289, 1, 0, 0, 0, 0, 291, 1, 0, 0, 0, 0, 293, 1, 0, 0, 0, 0, 295, 1, 0, 0, 0, 0, 297, 1, 0, 0, 0, 0, 299, 1, 0, 0, 0, 0, 301, 1, 0, 0, 0, 0, 303, 1, 0, 0, 0, 0, 305, 1, 0, 0, 0, 0, 307, 1, 0, 0, 0, 0, 309, 1, 0, 0, 0, 0, 311, 1, 0, 0, 0, 0, 313, 1, 0, 0, 0, 0, 315, 1, 0, 0, 0, 0, 317, 1, 0, 0, 0, 0, 319, 1, 0, 0, 0, 0, 321, 1, 0, 0, 0, 0, 323, 1, 0, 0, 0, 0, 325, 1, 0, 0, 0, 0, 327, 1, 0, 0, 0, 0, 329, 1, 0, 0, 0, 0, 331, 1, 0, 0, 0, 0, 333, 1, 0, 0, 0, 0, 335, 1, 0, 0, 0, 0, 337, 1, 0, 0, 0, 0, 339, 1, 0, 0, 0, 0, 341, 1, 0, 0, 0, 0, 343, 1, 0, 0, 0, 0, 347, 1, 0, 0, 0, 0, 349, 1, 0, 0, 0, 0, 351, 1, 0, 0, 0, 0, 353, 1, 0, 0, 0, 0, 359, 1, 0, 0, 0, 0, 361, 1, 0, 0, 0, 0, 363, 1, 0, 0, 0, 0, 365, 1, 0, 0, 0, 0, 367, 1, 0, 0, 0, 0, 369, 1, 0, 0, 0, 0, 371, 1, 0, 0, 0, 0, 373, 1, 0, 0, 0, 0, 375, 1, 0, 0, 0, 0, 377, 1, 0, 0, 0, 0, 379, 1, 0, 0, 0, 0, 381, 1, 0, 0, 0, 0, 383, 1, 0, 0, 0, 0, 387, 1, 0, 0, 0, 0, 391, 1, 0, 0, 0, 0, 395, 1, 0, 0, 0, 0, 407, 1, 0, 0, 0, 0, 413, 1, 0, 0, 0, 1, 415, 1, 0, 0, 0, 3, 422, 1, 0, 0, 0, 5, 427, 1, 0, 0, 0, 7, 437, 1, 0, 0, 0, 9, 444, 1, 0, 0, 0, 11, 451, 1, 0, 0, 0, 13, 462, 1, 0, 0, 0, 15, 467, 1, 0, 0, 0, 17, 473, 1, 0, 0, 0, 19, 480, 1, 0, 0, 0, 21, 485, 1, 0, 0, 0, 23, 492, 1, 0, 0, 0, 25, 503, 1, 0, 0, 0, 27, 508, 1, 0, 0, 0, 29, 524, 1, 0, 0, 0, 31, 528, 1, 0, 0, 0, 33, 540, 1, 0, 0, 0, 35, 546, 1, 0, 0, 0, 37, 554, 1, 0, 0, 0, 39, 562, 1, 0, 0, 0, 41, 571, 1, 0, 0, 0, 43, 579, 1, 0, 0, 0, 45, 588, 1, 0, 0, 0, 47, 598, 1, 0, 0, 0, 49, 609, 1, 0, 0, 0, 51, 623, 1, 0, 0, 0, 53, 633, 1, 0, 0, 0, 55, 644, 1, 0, 0, 0, 57, 656, 1, 0, 0, 0, 59, 664, 1, 0, 0, 0, 61, 674, 1, 0, 0, 0, 63, 683, 1, 0, 0, 0, 65, 694, 1, 0, 0, 0, 67, 703, 1, 0, 0, 0, 69, 713, 1, 0, 0, 0, 71, 723, 1, 0, 0, 0, 73, 731, 1, 0, 0, 0, 75, 740, 1, 0, 0, 0, 77, 748, 1, 0, 0, 0, 79, 762, 1, 0, 0, 0, 81, 770, 1, 0, 0, 0, 83, 773, 1, 0, 0, 0, 85, 778, 1, 0, 0, 0, 87, 786, 1, 0, 0, 0, 89, 789, 1, 0, 0, 0, 91, 795, 1, 0, 0, 0, 93, 800, 1, 0, 0, 0, 95, 802, 1, 0, 0, 0, 97, 804, 1, 0, 0, 0, 99, 812, 1, 0, 0, 0, 101, 814, 1, 0, 0, 0, 103, 816, 1, 0, 0, 0, 105, 818, 1, 0, 0, 0, 107, 826, 1, 0, 0, 0, 109, 834, 1, 0, 0, 0, 111, 836, 1, 0, 0, 0, 113, 838, 1, 0, 0, 0, 115, 841, 1, 0, 0, 0, 117, 844, 1, 0, 0, 0, 119, 852, 1, 0, 0, 0, 121, 860, 1, 0, 0, 0, 123, 862, 1, 0, 0, 0, 125, 864, 1, 0, 0, 0, 127, 872, 1, 0, 0, 0, 129, 880, 1, 0, 0, 0, 131, 882, 1, 0, 0, 0, 133, 889, 1, 0, 0, 0, 135, 896, 1, 0, 0, 0, 137, 902, 1, 0, 0, 0, 139, 905, 1, 0, 0, 0, 141, 913, 1, 0, 0, 0, 143, 921, 1, 0, 0, 0, 145, 931, 1, 0, 0, 0, 147, 941, 1, 0, 0, 0, 149, 948, 1, 0, 0, 0, 151, 955, 1, 0, 0, 0, 153, 965, 1, 0, 0, 0, 155, 975, 1, 0, 0, 0, 157, 981, 1, 0, 0, 0, 159, 988, 1, 0, 0, 0, 161, 995, 1, 0, 0, 0, 163, 1003, 1, 0, 0, 0, 165, 1063, 1, 0, 0, 0, 167, 1065, 1, 0, 0, 0, 169, 1070, 1, 0, 0, 0, 171, 1075, 1, 0, 0, 0, 173, 1081, 1, 0, 0, 0, 175, 1086, 1, 0, 0, 0, 177, 1090, 1, 0, 0, 0, 179, 1095, 1, 0, 0, 0, 181, 1100, 1, 0, 0, 0, 183, 1105, 1, 0, 0, 0, 185, 1110, 1, 0, 0, 0, 187, 1115, 1, 0, 0, 0, 189, 1120, 1, 0, 0, 0, 191, 1125, 1, 0, 0, 0, 193, 1133, 1, 0, 0, 0, 195, 1141, 1, 0, 0, 0, 197, 1149, 1, 0, 0, 0, 199, 1157, 1, 0, 0, 0, 201, 1165, 1, 0, 0, 0, 203, 1173, 1, 0, 0, 0, 205, 1179, 1, 0, 0, 0, 207, 1185, 1, 0, 0, 0, 209, 1191, 1, 0, 0, 0, 211, 1199, 1, 0, 0, 0, 213, 1207, 1, 0, 0, 0, 215, 1215, 1, 0, 0, 0, 217, 1224, 1, 0, 0, 0, 219, 1233, 1, 0, 0, 0, 221, 1242, 1, 0, 0, 0, 223, 1249, 1, 0, 0, 0, 225, 1257, 1, 0, 0, 0, 227, 1264, 1, 0, 0, 0, 229, 1272, 1, 0, 0, 0, 231, 1279, 1, 0, 0, 0, 233, 1287, 1, 0, 0, 0, 235, 1291, 1, 0, 0, 0, 237, 1295, 1, 0, 0, 0, 239, 1301, 1, 0, 0, 0, 241, 1306, 1, 0, 0, 0, 243, 1312, 1, 0, 0, 0, 245, 1317, 1, 0, 0, 0, 247, 1322, 1, 0, 0, 0, 249, 1329, 1, 0, 0, 0, 251, 1335, 1, 0, 0, 0, 253, 1340, 1, 0, 0, 0, 255, 1345, 1, 0, 0, 0, 257, 1350, 1, 0, 0, 0, 259, 1354, 1, 0, 0, 0, 261, 1360, 1, 0, 0, 0, 263, 1365, 1, 0, 0, 0, 265, 1370, 1, 0, 0, 0, 267, 1375, 1, 0, 0, 0, 269, 1380, 1, 0, 0, 0, 271, 1385, 1, 0, 0, 0, 273, 1397, 1, 0, 0, 0, 275, 1399, 1, 0, 0, 0, 277, 1404, 1, 0, 0, 0, 279, 1411, 1, 0, 0, 0, 281, 1450, 1, 0, 0, 0, 283, 1452, 1, 0, 0, 0, 285, 1481, 1, 0, 0, 0, 287, 1503, 1, 0, 0, 0, 289, 1527, 1, 0, 0, 0, 291, 1535, 1, 0, 0, 0, 293, 1537, 1, 0, 0, 0, 295, 1544, 1, 0, 0, 0, 297, 1550, 1, 0, 0, 0, 299, 1555, 1, 0, 0, 0, 301, 1581, 1, 0, 0, 0, 303, 1583, 1, 0, 0, 0, 305, 1591, 1, 0, 0, 0, 307, 1596, 1, 0, 0, 0, 309, 1604, 1, 0, 0, 0, 311, 1618, 1, 0, 0, 0, 313, 1625, 1, 0, 0, 0, 315, 1633, 1, 0, 0, 0, 317, 1641, 1, 0, 0, 0, 319, 1652, 1, 0, 0, 0, 321, 1654, 1, 0, 0, 0, 323, 1665, 1, 0, 0, 0, 325, 1674, 1, 0, 0, 0, 327, 1685, 1, 0, 0, 0, 329, 1694, 1, 0, 0, 0, 331, 1696, 1, 0, 0, 0, 333, 1699, 1, 0, 0, 0, 335, 1701, 1, 0, 0, 0, 337, 1703, 1, 0, 0, 0, 339, 1705, 1, 0, 0, 0, 341, 1707, 1, 0, 0, 0, 343, 1709, 1, 0, 0, 0, 345, 1711, 1, 0, 0, 0, 347, 1713, 1, 0, 0, 0, 349, 1743, 1, 0, 0, 0, 351, 1745, 1, 0, 0, 0, 353, 1747, 1, 0, 0, 0, 355, 1749, 1, 0, 0, 0, 357, 1751, 1, 0, 0, 0, 359, 1777, 1, 0, 0, 0, 361, 1815, 1, 0, 0, 0, 363, 1854, 1, 0, 0, 0, 365, 1856, 1, 0, 0, 0, 367, 1867, 1, 0, 0, 0, 369, 1871, 1, 0, 0, 0, 371, 1881, 1, 0, 0, 0, 373, 1883, 1, 0, 0, 0, 375, 1901, 1, 0, 0, 0, 377, 1903, 1, 0, 0, 0, 379, 1921, 1, 0, 0, 0, 381, 1945, 1, 0, 0, 0, 383, 1947, 1, 0, 0, 0, 385, 1949, 1, 0, 0, 0, 387, 1952, 1, 0, 0, 0, 389, 2340, 1, 0, 0, 0, 391, 2342, 1, 0, 0, 0, 393, 2696, 1, 0, 0, 0, 395, 2698, 1, 0, 0, 0, 397, 2702, 1, 0, 0, 0, 399, 2706, 1, 0, 0, 0, 401, 2713, 1, 0, 0, 0, 403, 2729, 1, 0, 0, 0, 405, 2731, 1, 0, 0, 0, 407, 2745, 1, 0, 0, 0, 409, 2747, 1, 0, 0, 0, 411, 2761, 1, 0, 0, 0, 413, 2788, 1, 0, 0, 0, 415, 416, 5, 92, 0, 0, 416, 417, 5, 97, 0, 0, 417, 418, 5, 99, 0, 0, 418, 419, 5, 117, 0, 0, 419, 420, 5, 116, 0, 0, 420, 421, 5, 101, 0, 0, 421, 2, 1, 0, 0, 0, 422, 423, 5, 92, 0, 0, 423, 424, 5, 98, 0, 0, 424, 425, 5, 97, 0, 0, 425, 426, 5, 114, 0, 0, 426, 4, 1, 0, 0, 0, 427, 428, 5, 92, 0, 0, 428, 429, 5, 111, 0, 0, 429, 430, 5, 118, 0, 0, 430, 431, 5, 101, 0, 0, 431, 432, 5, 114, 0, 0, 432, 433, 5, 108, 0, 0, 433, 434, 5, 105, 0, 0, 434, 435, 5, 110, 0, 0, 435, 436, 5, 101, 0, 0, 436, 6, 1, 0, 0, 0, 437, 438, 5, 92, 0, 0, 438, 439, 5, 98, 0, 0, 439, 440, 5, 114, 0, 0, 440, 441, 5, 101, 0, 0, 441, 442, 5, 118, 0, 0, 442, 443, 5, 101, 0, 0, 443, 8, 1, 0, 0, 0, 444, 445, 5, 92, 0, 0, 445, 446, 5, 99, 0, 0, 446, 447, 5, 104, 0, 0, 447, 448, 5, 101, 0, 0, 448, 449, 5, 99, 0, 0, 449, 450, 5, 107, 0, 0, 450, 10, 1, 0, 0, 0, 451, 452, 5, 92, 0, 0, 452, 453, 5, 119, 0, 0, 453, 454, 5, 105, 0, 0, 454, 455, 5, 100, 0, 0, 455, 456, 5, 101, 0, 0, 456, 457, 5, 99, 0, 0, 457, 458, 5, 104, 0, 0, 458, 459, 5, 101, 0, 0, 459, 460, 5, 99, 0, 0, 460, 461, 5, 107, 0, 0, 461, 12, 1, 0, 0, 0, 462, 463, 5, 92, 0, 0, 463, 464, 5, 100, 0, 0, 464, 465, 5, 111, 0, 0, 465, 466, 5, 116, 0, 0, 466, 14, 1, 0, 0, 0, 467, 468, 5, 92, 0, 0, 468, 469, 5, 100, 0, 0, 469, 470, 5, 100, 0, 0, 470, 471, 5, 111, 0, 0, 471, 472, 5, 116, 0, 0, 472, 16, 1, 0, 0, 0, 473, 474, 5, 92, 0, 0, 474, 475, 5, 103, 0, 0, 475, 476, 5, 114, 0, 0, 476, 477, 5, 97, 0, 0, 477, 478, 5, 118, 0, 0, 478, 479, 5, 101, 0, 0, 479, 18, 1, 0, 0, 0, 480, 481, 5, 92, 0, 0, 481, 482, 5, 104, 0, 0, 482, 483, 5, 97, 0, 0, 483, 484, 5, 116, 0, 0, 484, 20, 1, 0, 0, 0, 485, 486, 5, 92, 0, 0, 486, 487, 5, 116, 0, 0, 487, 488, 5, 105, 0, 0, 488, 489, 5, 108, 0, 0, 489, 490, 5, 100, 0, 0, 490, 491, 5, 101, 0, 0, 491, 22, 1, 0, 0, 0, 492, 493, 5, 92, 0, 0, 493, 494, 5, 119, 0, 0, 494, 495, 5, 105, 0, 0, 495, 496, 5, 100, 0, 0, 496, 497, 5, 101, 0, 0, 497, 498, 5, 116, 0, 0, 498, 499, 5, 105, 0, 0, 499, 500, 5, 108, 0, 0, 500, 501, 5, 100, 0, 0, 501, 502, 5, 101, 0, 0, 502, 24, 1, 0, 0, 0, 503, 504, 5, 92, 0, 0, 504, 505, 5, 118, 0, 0, 505, 506, 5, 101, 0, 0, 506, 507, 5, 99, 0, 0, 507, 26, 1, 0, 0, 0, 508, 509, 5, 92, 0, 0, 509, 510, 5, 111, 0, 0, 510, 511, 5, 118, 0, 0, 511, 512, 5, 101, 0, 0, 512, 513, 5, 114, 0, 0, 513, 514, 5, 114, 0, 0, 514, 515, 5, 105, 0, 0, 515, 516, 5, 103, 0, 0, 516, 517, 5, 104, 0, 0, 517, 518, 5, 116, 0, 0, 518, 519, 5, 97, 0, 0, 519, 520, 5, 114, 0, 0, 520, 521, 5, 114, 0, 0, 521, 522, 5, 111, 0, 0, 522, 523, 5, 119, 0, 0, 523, 28, 1, 0, 0, 0, 524, 525, 5, 92, 0, 0, 525, 526, 5, 98, 0, 0, 526, 527, 5, 109, 0, 0, 527, 30, 1, 0, 0, 0, 528, 529, 5, 92, 0, 0, 529, 530, 5, 98, 0, 0, 530, 531, 5, 111, 0, 0, 531, 532, 5, 108, 0, 0, 532, 533, 5, 100, 0, 0, 533, 534, 5, 115, 0, 0, 534, 535, 5, 121, 0, 0, 535, 536, 5, 109, 0, 0, 536, 537, 5, 98, 0, 0, 537, 538, 5, 111, 0, 0, 538, 539, 5, 108, 0, 0, 539, 32, 1, 0, 0, 0, 540, 541, 5, 92, 0, 0, 541, 542, 5, 116, 0, 0, 542, 543, 5, 101, 0, 0, 543, 544, 5, 120, 0, 0, 544, 545, 5, 116, 0, 0, 545, 34, 1, 0, 0, 0, 546, 547, 5, 92, 0, 0, 547, 548, 5, 116, 0, 0, 548, 549, 5, 101, 0, 0, 549, 550, 5, 120, 0, 0, 550, 551, 5, 116, 0, 0, 551, 552, 5, 105, 0, 0, 552, 553, 5, 116, 0, 0, 553, 36, 1, 0, 0, 0, 554, 555, 5, 92, 0, 0, 555, 556, 5, 109, 0, 0, 556, 557, 5, 97, 0, 0, 557, 558, 5, 116, 0, 0, 558, 559, 5, 104, 0, 0, 559, 560, 5, 98, 0, 0, 560, 561, 5, 98, 0, 0, 561, 38, 1, 0, 0, 0, 562, 563, 5, 92, 0, 0, 563, 564, 5, 109, 0, 0, 564, 565, 5, 97, 0, 0, 565, 566, 5, 116, 0, 0, 566, 567, 5, 104, 0, 0, 567, 568, 5, 98, 0, 0, 568, 569, 5, 105, 0, 0, 569, 570, 5, 110, 0, 0, 570, 40, 1, 0, 0, 0, 571, 572, 5, 92, 0, 0, 572, 573, 5, 109, 0, 0, 573, 574, 5, 97, 0, 0, 574, 575, 5, 116, 0, 0, 575, 576, 5, 104, 0, 0, 576, 577, 5, 98, 0, 0, 577, 578, 5, 102, 0, 0, 578, 42, 1, 0, 0, 0, 579, 580, 5, 92, 0, 0, 580, 581, 5, 109, 0, 0, 581, 582, 5, 97, 0, 0, 582, 583, 5, 116, 0, 0, 583, 584, 5, 104, 0, 0, 584, 585, 5, 99, 0, 0, 585, 586, 5, 97, 0, 0, 586, 587, 5, 108, 0, 0, 587, 44, 1, 0, 0, 0, 588, 589, 5, 92, 0, 0, 589, 590, 5, 109, 0, 0, 590, 591, 5, 97, 0, 0, 591, 592, 5, 116, 0, 0, 592, 593, 5, 104, 0, 0, 593, 594, 5, 99, 0, 0, 594, 595, 5, 108, 0, 0, 595, 596, 5, 97, 0, 0, 596, 597, 5, 112, 0, 0, 597, 46, 1, 0, 0, 0, 598, 599, 5, 92, 0, 0, 599, 600, 5, 109, 0, 0, 600, 601, 5, 97, 0, 0, 601, 602, 5, 116, 0, 0, 602, 603, 5, 104, 0, 0, 603, 604, 5, 99, 0, 0, 604, 605, 5, 108, 0, 0, 605, 606, 5, 111, 0, 0, 606, 607, 5, 115, 0, 0, 607, 608, 5, 101, 0, 0, 608, 48, 1, 0, 0, 0, 609, 610, 5, 92, 0, 0, 610, 611, 5, 109, 0, 0, 611, 612, 5, 97, 0, 0, 612, 613, 5, 116, 0, 0, 613, 614, 5, 104, 0, 0, 614, 615, 5, 101, 0, 0, 615, 616, 5, 108, 0, 0, 616, 617, 5, 108, 0, 0, 617, 618, 5, 105, 0, 0, 618, 619, 5, 112, 0, 0, 619, 620, 5, 115, 0, 0, 620, 621, 5, 105, 0, 0, 621, 622, 5, 115, 0, 0, 622, 50, 1, 0, 0, 0, 623, 624, 5, 92, 0, 0, 624, 625, 5, 109, 0, 0, 625, 626, 5, 97, 0, 0, 626, 627, 5, 116, 0, 0, 627, 628, 5, 104, 0, 0, 628, 629, 5, 102, 0, 0, 629, 630, 5, 114, 0, 0, 630, 631, 5, 97, 0, 0, 631, 632, 5, 107, 0, 0, 632, 52, 1, 0, 0, 0, 633, 634, 5, 92, 0, 0, 634, 635, 5, 109, 0, 0, 635, 636, 5, 97, 0, 0, 636, 637, 5, 116, 0, 0, 637, 638, 5, 104, 0, 0, 638, 639, 5, 105, 0, 0, 639, 640, 5, 110, 0, 0, 640, 641, 5, 110, 0, 0, 641, 642, 5, 101, 0, 0, 642, 643, 5, 114, 0, 0, 643, 54, 1, 0, 0, 0, 644, 645, 5, 92, 0, 0, 645, 646, 5, 109, 0, 0, 646, 647, 5, 97, 0, 0, 647, 648, 5, 116, 0, 0, 648, 649, 5, 104, 0, 0, 649, 650, 5, 110, 0, 0, 650, 651, 5, 111, 0, 0, 651, 652, 5, 114, 0, 0, 652, 653, 5, 109, 0, 0, 653, 654, 5, 97, 0, 0, 654, 655, 5, 108, 0, 0, 655, 56, 1, 0, 0, 0, 656, 657, 5, 92, 0, 0, 657, 658, 5, 109, 0, 0, 658, 659, 5, 97, 0, 0, 659, 660, 5, 116, 0, 0, 660, 661, 5, 104, 0, 0, 661, 662, 5, 111, 0, 0, 662, 663, 5, 112, 0, 0, 663, 58, 1, 0, 0, 0, 664, 665, 5, 92, 0, 0, 665, 666, 5, 109, 0, 0, 666, 667, 5, 97, 0, 0, 667, 668, 5, 116, 0, 0, 668, 669, 5, 104, 0, 0, 669, 670, 5, 111, 0, 0, 670, 671, 5, 112, 0, 0, 671, 672, 5, 101, 0, 0, 672, 673, 5, 110, 0, 0, 673, 60, 1, 0, 0, 0, 674, 675, 5, 92, 0, 0, 675, 676, 5, 109, 0, 0, 676, 677, 5, 97, 0, 0, 677, 678, 5, 116, 0, 0, 678, 679, 5, 104, 0, 0, 679, 680, 5, 111, 0, 0, 680, 681, 5, 114, 0, 0, 681, 682, 5, 100, 0, 0, 682, 62, 1, 0, 0, 0, 683, 684, 5, 92, 0, 0, 684, 685, 5, 109, 0, 0, 685, 686, 5, 97, 0, 0, 686, 687, 5, 116, 0, 0, 687, 688, 5, 104, 0, 0, 688, 689, 5, 112, 0, 0, 689, 690, 5, 117, 0, 0, 690, 691, 5, 110, 0, 0, 691, 692, 5, 99, 0, 0, 692, 693, 5, 116, 0, 0, 693, 64, 1, 0, 0, 0, 694, 695, 5, 92, 0, 0, 695, 696, 5, 109, 0, 0, 696, 697, 5, 97, 0, 0, 697, 698, 5, 116, 0, 0, 698, 699, 5, 104, 0, 0, 699, 700, 5, 114, 0, 0, 700, 701, 5, 101, 0, 0, 701, 702, 5, 108, 0, 0, 702, 66, 1, 0, 0, 0, 703, 704, 5, 92, 0, 0, 704, 705, 5, 109, 0, 0, 705, 706, 5, 97, 0, 0, 706, 707, 5, 116, 0, 0, 707, 708, 5, 104, 0, 0, 708, 709, 5, 114, 0, 0, 709, 710, 5, 105, 0, 0, 710, 711, 5, 110, 0, 0, 711, 712, 5, 103, 0, 0, 712, 68, 1, 0, 0, 0, 713, 714, 5, 92, 0, 0, 714, 715, 5, 109, 0, 0, 715, 716, 5, 97, 0, 0, 716, 717, 5, 116, 0, 0, 717, 718, 5, 104, 0, 0, 718, 719, 5, 114, 0, 0, 719, 720, 5, 108, 0, 0, 720, 721, 5, 97, 0, 0, 721, 722, 5, 112, 0, 0, 722, 70, 1, 0, 0, 0, 723, 724, 5, 92, 0, 0, 724, 725, 5, 109, 0, 0, 725, 726, 5, 97, 0, 0, 726, 727, 5, 116, 0, 0, 727, 728, 5, 104, 0, 0, 728, 729, 5, 114, 0, 0, 729, 730, 5, 109, 0, 0, 730, 72, 1, 0, 0, 0, 731, 732, 5, 92, 0, 0, 732, 733, 5, 109, 0, 0, 733, 734, 5, 97, 0, 0, 734, 735, 5, 116, 0, 0, 735, 736, 5, 104, 0, 0, 736, 737, 5, 115, 0, 0, 737, 738, 5, 99, 0, 0, 738, 739, 5, 114, 0, 0, 739, 74, 1, 0, 0, 0, 740, 741, 5, 92, 0, 0, 741, 742, 5, 109, 0, 0, 742, 743, 5, 97, 0, 0, 743, 744, 5, 116, 0, 0, 744, 745, 5, 104, 0, 0, 745, 746, 5, 115, 0, 0, 746, 747, 5, 102, 0, 0, 747, 76, 1, 0, 0, 0, 748, 749, 5, 92, 0, 0, 749, 750, 5, 109, 0, 0, 750, 751, 5, 97, 0, 0, 751, 752, 5, 116, 0, 0, 752, 753, 5, 104, 0, 0, 753, 754, 5, 115, 0, 0, 754, 755, 5, 116, 0, 0, 755, 756, 5, 101, 0, 0, 756, 757, 5, 114, 0, 0, 757, 758, 5, 108, 0, 0, 758, 759, 5, 105, 0, 0, 759, 760, 5, 110, 0, 0, 760, 761, 5, 103, 0, 0, 761, 78, 1, 0, 0, 0, 762, 763, 5, 92, 0, 0, 763, 764, 5, 109, 0, 0, 764, 765, 5, 97, 0, 0, 765, 766, 5, 116, 0, 0, 766, 767, 5, 104, 0, 0, 767, 768, 5, 116, 0, 0, 768, 769, 5, 116, 0, 0, 769, 80, 1, 0, 0, 0, 770, 771, 5, 94, 0, 0, 771, 772, 5, 84, 0, 0, 772, 82, 1, 0, 0, 0, 773, 774, 5, 94, 0, 0, 774, 775, 5, 123, 0, 0, 775, 776, 5, 84, 0, 0, 776, 777, 5, 125, 0, 0, 777, 84, 1, 0, 0, 0, 778, 779, 5, 94, 0, 0, 779, 780, 5, 123, 0, 0, 780, 781, 5, 92, 0, 0, 781, 782, 5, 116, 0, 0, 782, 783, 5, 111, 0, 0, 783, 784, 5, 112, 0, 0, 784, 785, 5, 125, 0, 0, 785, 86, 1, 0, 0, 0, 786, 787, 5, 39, 0, 0, 787, 88, 1, 0, 0, 0, 788, 790, 7, 0, 0, 0, 789, 788, 1, 0, 0, 0, 790, 791, 1, 0, 0, 0, 791, 789, 1, 0, 0, 0, 791, 792, 1, 0, 0, 0, 792, 793, 1, 0, 0, 0, 793, 794, 6, 44, 0, 0, 794, 90, 1, 0, 0, 0, 795, 796, 5, 92, 0, 0, 796, 797, 5, 36, 0, 0, 797, 798, 1, 0, 0, 0, 798, 799, 6, 45, 0, 0, 799, 92, 1, 0, 0, 0, 800, 801, 5, 43, 0, 0, 801, 94, 1, 0, 0, 0, 802, 803, 5, 45, 0, 0, 803, 96, 1, 0, 0, 0, 804, 805, 5, 42, 0, 0, 805, 98, 1, 0, 0, 0, 806, 813, 5, 47, 0, 0, 807, 808, 5, 92, 0, 0, 808, 809, 5, 111, 0, 0, 809, 810, 5, 118, 0, 0, 810, 811, 5, 101, 0, 0, 811, 813, 5, 114, 0, 0, 812, 806, 1, 0, 0, 0, 812, 807, 1, 0, 0, 0, 813, 100, 1, 0, 0, 0, 814, 815, 5, 40, 0, 0, 815, 102, 1, 0, 0, 0, 816, 817, 5, 41, 0, 0, 817, 104, 1, 0, 0, 0, 818, 819, 5, 92, 0, 0, 819, 820, 5, 108, 0, 0, 820, 821, 5, 103, 0, 0, 821, 822, 5, 114, 0, 0, 822, 823, 5, 111, 0, 0, 823, 824, 5, 117, 0, 0, 824, 825, 5, 112, 0, 0, 825, 106, 1, 0, 0, 0, 826, 827, 5, 92, 0, 0, 827, 828, 5, 114, 0, 0, 828, 829, 5, 103, 0, 0, 829, 830, 5, 114, 0, 0, 830, 831, 5, 111, 0, 0, 831, 832, 5, 117, 0, 0, 832, 833, 5, 112, 0, 0, 833, 108, 1, 0, 0, 0, 834, 835, 5, 123, 0, 0, 835, 110, 1, 0, 0, 0, 836, 837, 5, 125, 0, 0, 837, 112, 1, 0, 0, 0, 838, 839, 5, 92, 0, 0, 839, 840, 5, 123, 0, 0, 840, 114, 1, 0, 0, 0, 841, 842, 5, 92, 0, 0, 842, 843, 5, 125, 0, 0, 843, 116, 1, 0, 0, 0, 844, 845, 5, 92, 0, 0, 845, 846, 5, 108, 0, 0, 846, 847, 5, 98, 0, 0, 847, 848, 5, 114, 0, 0, 848, 849, 5, 97, 0, 0, 849, 850, 5, 99, 0, 0, 850, 851, 5, 101, 0, 0, 851, 118, 1, 0, 0, 0, 852, 853, 5, 92, 0, 0, 853, 854, 5, 114, 0, 0, 854, 855, 5, 98, 0, 0, 855, 856, 5, 114, 0, 0, 856, 857, 5, 97, 0, 0, 857, 858, 5, 99, 0, 0, 858, 859, 5, 101, 0, 0, 859, 120, 1, 0, 0, 0, 860, 861, 5, 91, 0, 0, 861, 122, 1, 0, 0, 0, 862, 863, 5, 93, 0, 0, 863, 124, 1, 0, 0, 0, 864, 865, 5, 92, 0, 0, 865, 866, 5, 108, 0, 0, 866, 867, 5, 98, 0, 0, 867, 868, 5, 114, 0, 0, 868, 869, 5, 97, 0, 0, 869, 870, 5, 99, 0, 0, 870, 871, 5, 107, 0, 0, 871, 126, 1, 0, 0, 0, 872, 873, 5, 92, 0, 0, 873, 874, 5, 114, 0, 0, 874, 875, 5, 98, 0, 0, 875, 876, 5, 114, 0, 0, 876, 877, 5, 97, 0, 0, 877, 878, 5, 99, 0, 0, 878, 879, 5, 107, 0, 0, 879, 128, 1, 0, 0, 0, 880, 881, 5, 124, 0, 0, 881, 130, 1, 0, 0, 0, 882, 883, 5, 92, 0, 0, 883, 884, 5, 108, 0, 0, 884, 885, 5, 118, 0, 0, 885, 886, 5, 101, 0, 0, 886, 887, 5, 114, 0, 0, 887, 888, 5, 116, 0, 0, 888, 132, 1, 0, 0, 0, 889, 890, 5, 92, 0, 0, 890, 891, 5, 114, 0, 0, 891, 892, 5, 118, 0, 0, 892, 893, 5, 101, 0, 0, 893, 894, 5, 114, 0, 0, 894, 895, 5, 116, 0, 0, 895, 134, 1, 0, 0, 0, 896, 897, 5, 92, 0, 0, 897, 898, 5, 118, 0, 0, 898, 899, 5, 101, 0, 0, 899, 900, 5, 114, 0, 0, 900, 901, 5, 116, 0, 0, 901, 136, 1, 0, 0, 0, 902, 903, 5, 92, 0, 0, 903, 904, 5, 124, 0, 0, 904, 138, 1, 0, 0, 0, 905, 906, 5, 92, 0, 0, 906, 907, 5, 108, 0, 0, 907, 908, 5, 102, 0, 0, 908, 909, 5, 108, 0, 0, 909, 910, 5, 111, 0, 0, 910, 911, 5, 111, 0, 0, 911, 912, 5, 114, 0, 0, 912, 140, 1, 0, 0, 0, 913, 914, 5, 92, 0, 0, 914, 915, 5, 114, 0, 0, 915, 916, 5, 102, 0, 0, 916, 917, 5, 108, 0, 0, 917, 918, 5, 111, 0, 0, 918, 919, 5, 111, 0, 0, 919, 920, 5, 114, 0, 0, 920, 142, 1, 0, 0, 0, 921, 922, 5, 92, 0, 0, 922, 923, 5, 108, 0, 0, 923, 924, 5, 108, 0, 0, 924, 925, 5, 99, 0, 0, 925, 926, 5, 111, 0, 0, 926, 927, 5, 114, 0, 0, 927, 928, 5, 110, 0, 0, 928, 929, 5, 101, 0, 0, 929, 930, 5, 114, 0, 0, 930, 144, 1, 0, 0, 0, 931, 932, 5, 92, 0, 0, 932, 933, 5, 108, 0, 0, 933, 934, 5, 114, 0, 0, 934, 935, 5, 99, 0, 0, 935, 936, 5, 111, 0, 0, 936, 937, 5, 114, 0, 0, 937, 938, 5, 110, 0, 0, 938, 939, 5, 101, 0, 0, 939, 940, 5, 114, 0, 0, 940, 146, 1, 0, 0, 0, 941, 942, 5, 92, 0, 0, 942, 943, 5, 108, 0, 0, 943, 944, 5, 99, 0, 0, 944, 945, 5, 101, 0, 0, 945, 946, 5, 105, 0, 0, 946, 947, 5, 108, 0, 0, 947, 148, 1, 0, 0, 0, 948, 949, 5, 92, 0, 0, 949, 950, 5, 114, 0, 0, 950, 951, 5, 99, 0, 0, 951, 952, 5, 101, 0, 0, 952, 953, 5, 105, 0, 0, 953, 954, 5, 108, 0, 0, 954, 150, 1, 0, 0, 0, 955, 956, 5, 92, 0, 0, 956, 957, 5, 117, 0, 0, 957, 958, 5, 108, 0, 0, 958, 959, 5, 99, 0, 0, 959, 960, 5, 111, 0, 0, 960, 961, 5, 114, 0, 0, 961, 962, 5, 110, 0, 0, 962, 963, 5, 101, 0, 0, 963, 964, 5, 114, 0, 0, 964, 152, 1, 0, 0, 0, 965, 966, 5, 92, 0, 0, 966, 967, 5, 117, 0, 0, 967, 968, 5, 114, 0, 0, 968, 969, 5, 99, 0, 0, 969, 970, 5, 111, 0, 0, 970, 971, 5, 114, 0, 0, 971, 972, 5, 110, 0, 0, 972, 973, 5, 101, 0, 0, 973, 974, 5, 114, 0, 0, 974, 154, 1, 0, 0, 0, 975, 976, 5, 92, 0, 0, 976, 977, 5, 108, 0, 0, 977, 978, 5, 101, 0, 0, 978, 979, 5, 102, 0, 0, 979, 980, 5, 116, 0, 0, 980, 156, 1, 0, 0, 0, 981, 982, 5, 92, 0, 0, 982, 983, 5, 114, 0, 0, 983, 984, 5, 105, 0, 0, 984, 985, 5, 103, 0, 0, 985, 986, 5, 104, 0, 0, 986, 987, 5, 116, 0, 0, 987, 158, 1, 0, 0, 0, 988, 989, 5, 92, 0, 0, 989, 990, 5, 109, 0, 0, 990, 991, 5, 108, 0, 0, 991, 992, 5, 101, 0, 0, 992, 993, 5, 102, 0, 0, 993, 994, 5, 116, 0, 0, 994, 160, 1, 0, 0, 0, 995, 996, 5, 92, 0, 0, 996, 997, 5, 109, 0, 0, 997, 998, 5, 114, 0, 0, 998, 999, 5, 105, 0, 0, 999, 1000, 5, 103, 0, 0, 1000, 1001, 5, 104, 0, 0, 1001, 1002, 5, 116, 0, 0, 1002, 162, 1, 0, 0, 0, 1003, 1004, 5, 92, 0, 0, 1004, 1005, 5, 108, 0, 0, 1005, 1006, 5, 105, 0, 0, 1006, 1007, 5, 109, 0, 0, 1007, 164, 1, 0, 0, 0, 1008, 1009, 5, 92, 0, 0, 1009, 1010, 5, 116, 0, 0, 1010, 1064, 5, 111, 0, 0, 1011, 1012, 5, 92, 0, 0, 1012, 1013, 5, 114, 0, 0, 1013, 1014, 5, 105, 0, 0, 1014, 1015, 5, 103, 0, 0, 1015, 1016, 5, 104, 0, 0, 1016, 1017, 5, 116, 0, 0, 1017, 1018, 5, 97, 0, 0, 1018, 1019, 5, 114, 0, 0, 1019, 1020, 5, 114, 0, 0, 1020, 1021, 5, 111, 0, 0, 1021, 1064, 5, 119, 0, 0, 1022, 1023, 5, 92, 0, 0, 1023, 1024, 5, 82, 0, 0, 1024, 1025, 5, 105, 0, 0, 1025, 1026, 5, 103, 0, 0, 1026, 1027, 5, 104, 0, 0, 1027, 1028, 5, 116, 0, 0, 1028, 1029, 5, 97, 0, 0, 1029, 1030, 5, 114, 0, 0, 1030, 1031, 5, 114, 0, 0, 1031, 1032, 5, 111, 0, 0, 1032, 1064, 5, 119, 0, 0, 1033, 1034, 5, 92, 0, 0, 1034, 1035, 5, 108, 0, 0, 1035, 1036, 5, 111, 0, 0, 1036, 1037, 5, 110, 0, 0, 1037, 1038, 5, 103, 0, 0, 1038, 1039, 5, 114, 0, 0, 1039, 1040, 5, 105, 0, 0, 1040, 1041, 5, 103, 0, 0, 1041, 1042, 5, 104, 0, 0, 1042, 1043, 5, 116, 0, 0, 1043, 1044, 5, 97, 0, 0, 1044, 1045, 5, 114, 0, 0, 1045, 1046, 5, 114, 0, 0, 1046, 1047, 5, 111, 0, 0, 1047, 1064, 5, 119, 0, 0, 1048, 1049, 5, 92, 0, 0, 1049, 1050, 5, 76, 0, 0, 1050, 1051, 5, 111, 0, 0, 1051, 1052, 5, 110, 0, 0, 1052, 1053, 5, 103, 0, 0, 1053, 1054, 5, 114, 0, 0, 1054, 1055, 5, 105, 0, 0, 1055, 1056, 5, 103, 0, 0, 1056, 1057, 5, 104, 0, 0, 1057, 1058, 5, 116, 0, 0, 1058, 1059, 5, 97, 0, 0, 1059, 1060, 5, 114, 0, 0, 1060, 1061, 5, 114, 0, 0, 1061, 1062, 5, 111, 0, 0, 1062, 1064, 5, 119, 0, 0, 1063, 1008, 1, 0, 0, 0, 1063, 1011, 1, 0, 0, 0, 1063, 1022, 1, 0, 0, 0, 1063, 1033, 1, 0, 0, 0, 1063, 1048, 1, 0, 0, 0, 1064, 166, 1, 0, 0, 0, 1065, 1066, 5, 92, 0, 0, 1066, 1067, 5, 105, 0, 0, 1067, 1068, 5, 110, 0, 0, 1068, 1069, 5, 116, 0, 0, 1069, 168, 1, 0, 0, 0, 1070, 1071, 5, 92, 0, 0, 1071, 1072, 5, 115, 0, 0, 1072, 1073, 5, 117, 0, 0, 1073, 1074, 5, 109, 0, 0, 1074, 170, 1, 0, 0, 0, 1075, 1076, 5, 92, 0, 0, 1076, 1077, 5, 112, 0, 0, 1077, 1078, 5, 114, 0, 0, 1078, 1079, 5, 111, 0, 0, 1079, 1080, 5, 100, 0, 0, 1080, 172, 1, 0, 0, 0, 1081, 1082, 5, 92, 0, 0, 1082, 1083, 5, 108, 0, 0, 1083, 1084, 5, 111, 0, 0, 1084, 1085, 5, 103, 0, 0, 1085, 174, 1, 0, 0, 0, 1086, 1087, 5, 92, 0, 0, 1087, 1088, 5, 108, 0, 0, 1088, 1089, 5, 110, 0, 0, 1089, 176, 1, 0, 0, 0, 1090, 1091, 5, 92, 0, 0, 1091, 1092, 5, 101, 0, 0, 1092, 1093, 5, 120, 0, 0, 1093, 1094, 5, 112, 0, 0, 1094, 178, 1, 0, 0, 0, 1095, 1096, 5, 92, 0, 0, 1096, 1097, 5, 115, 0, 0, 1097, 1098, 5, 105, 0, 0, 1098, 1099, 5, 110, 0, 0, 1099, 180, 1, 0, 0, 0, 1100, 1101, 5, 92, 0, 0, 1101, 1102, 5, 99, 0, 0, 1102, 1103, 5, 111, 0, 0, 1103, 1104, 5, 115, 0, 0, 1104, 182, 1, 0, 0, 0, 1105, 1106, 5, 92, 0, 0, 1106, 1107, 5, 116, 0, 0, 1107, 1108, 5, 97, 0, 0, 1108, 1109, 5, 110, 0, 0, 1109, 184, 1, 0, 0, 0, 1110, 1111, 5, 92, 0, 0, 1111, 1112, 5, 99, 0, 0, 1112, 1113, 5, 115, 0, 0, 1113, 1114, 5, 99, 0, 0, 1114, 186, 1, 0, 0, 0, 1115, 1116, 5, 92, 0, 0, 1116, 1117, 5, 115, 0, 0, 1117, 1118, 5, 101, 0, 0, 1118, 1119, 5, 99, 0, 0, 1119, 188, 1, 0, 0, 0, 1120, 1121, 5, 92, 0, 0, 1121, 1122, 5, 99, 0, 0, 1122, 1123, 5, 111, 0, 0, 1123, 1124, 5, 116, 0, 0, 1124, 190, 1, 0, 0, 0, 1125, 1126, 5, 92, 0, 0, 1126, 1127, 5, 97, 0, 0, 1127, 1128, 5, 114, 0, 0, 1128, 1129, 5, 99, 0, 0, 1129, 1130, 5, 115, 0, 0, 1130, 1131, 5, 105, 0, 0, 1131, 1132, 5, 110, 0, 0, 1132, 192, 1, 0, 0, 0, 1133, 1134, 5, 92, 0, 0, 1134, 1135, 5, 97, 0, 0, 1135, 1136, 5, 114, 0, 0, 1136, 1137, 5, 99, 0, 0, 1137, 1138, 5, 99, 0, 0, 1138, 1139, 5, 111, 0, 0, 1139, 1140, 5, 115, 0, 0, 1140, 194, 1, 0, 0, 0, 1141, 1142, 5, 92, 0, 0, 1142, 1143, 5, 97, 0, 0, 1143, 1144, 5, 114, 0, 0, 1144, 1145, 5, 99, 0, 0, 1145, 1146, 5, 116, 0, 0, 1146, 1147, 5, 97, 0, 0, 1147, 1148, 5, 110, 0, 0, 1148, 196, 1, 0, 0, 0, 1149, 1150, 5, 92, 0, 0, 1150, 1151, 5, 97, 0, 0, 1151, 1152, 5, 114, 0, 0, 1152, 1153, 5, 99, 0, 0, 1153, 1154, 5, 99, 0, 0, 1154, 1155, 5, 115, 0, 0, 1155, 1156, 5, 99, 0, 0, 1156, 198, 1, 0, 0, 0, 1157, 1158, 5, 92, 0, 0, 1158, 1159, 5, 97, 0, 0, 1159, 1160, 5, 114, 0, 0, 1160, 1161, 5, 99, 0, 0, 1161, 1162, 5, 115, 0, 0, 1162, 1163, 5, 101, 0, 0, 1163, 1164, 5, 99, 0, 0, 1164, 200, 1, 0, 0, 0, 1165, 1166, 5, 92, 0, 0, 1166, 1167, 5, 97, 0, 0, 1167, 1168, 5, 114, 0, 0, 1168, 1169, 5, 99, 0, 0, 1169, 1170, 5, 99, 0, 0, 1170, 1171, 5, 111, 0, 0, 1171, 1172, 5, 116, 0, 0, 1172, 202, 1, 0, 0, 0, 1173, 1174, 5, 92, 0, 0, 1174, 1175, 5, 115, 0, 0, 1175, 1176, 5, 105, 0, 0, 1176, 1177, 5, 110, 0, 0, 1177, 1178, 5, 104, 0, 0, 1178, 204, 1, 0, 0, 0, 1179, 1180, 5, 92, 0, 0, 1180, 1181, 5, 99, 0, 0, 1181, 1182, 5, 111, 0, 0, 1182, 1183, 5, 115, 0, 0, 1183, 1184, 5, 104, 0, 0, 1184, 206, 1, 0, 0, 0, 1185, 1186, 5, 92, 0, 0, 1186, 1187, 5, 116, 0, 0, 1187, 1188, 5, 97, 0, 0, 1188, 1189, 5, 110, 0, 0, 1189, 1190, 5, 104, 0, 0, 1190, 208, 1, 0, 0, 0, 1191, 1192, 5, 92, 0, 0, 1192, 1193, 5, 97, 0, 0, 1193, 1194, 5, 114, 0, 0, 1194, 1195, 5, 115, 0, 0, 1195, 1196, 5, 105, 0, 0, 1196, 1197, 5, 110, 0, 0, 1197, 1198, 5, 104, 0, 0, 1198, 210, 1, 0, 0, 0, 1199, 1200, 5, 92, 0, 0, 1200, 1201, 5, 97, 0, 0, 1201, 1202, 5, 114, 0, 0, 1202, 1203, 5, 99, 0, 0, 1203, 1204, 5, 111, 0, 0, 1204, 1205, 5, 115, 0, 0, 1205, 1206, 5, 104, 0, 0, 1206, 212, 1, 0, 0, 0, 1207, 1208, 5, 92, 0, 0, 1208, 1209, 5, 97, 0, 0, 1209, 1210, 5, 114, 0, 0, 1210, 1211, 5, 116, 0, 0, 1211, 1212, 5, 97, 0, 0, 1212, 1213, 5, 110, 0, 0, 1213, 1214, 5, 104, 0, 0, 1214, 214, 1, 0, 0, 0, 1215, 1216, 5, 92, 0, 0, 1216, 1217, 5, 97, 0, 0, 1217, 1218, 5, 114, 0, 0, 1218, 1219, 5, 99, 0, 0, 1219, 1220, 5, 115, 0, 0, 1220, 1221, 5, 105, 0, 0, 1221, 1222, 5, 110, 0, 0, 1222, 1223, 5, 104, 0, 0, 1223, 216, 1, 0, 0, 0, 1224, 1225, 5, 92, 0, 0, 1225, 1226, 5, 97, 0, 0, 1226, 1227, 5, 114, 0, 0, 1227, 1228, 5, 99, 0, 0, 1228, 1229, 5, 99, 0, 0, 1229, 1230, 5, 111, 0, 0, 1230, 1231, 5, 115, 0, 0, 1231, 1232, 5, 104, 0, 0, 1232, 218, 1, 0, 0, 0, 1233, 1234, 5, 92, 0, 0, 1234, 1235, 5, 97, 0, 0, 1235, 1236, 5, 114, 0, 0, 1236, 1237, 5, 99, 0, 0, 1237, 1238, 5, 116, 0, 0, 1238, 1239, 5, 97, 0, 0, 1239, 1240, 5, 110, 0, 0, 1240, 1241, 5, 104, 0, 0, 1241, 220, 1, 0, 0, 0, 1242, 1243, 5, 97, 0, 0, 1243, 1244, 5, 114, 0, 0, 1244, 1245, 5, 115, 0, 0, 1245, 1246, 5, 105, 0, 0, 1246, 1247, 5, 110, 0, 0, 1247, 1248, 5, 104, 0, 0, 1248, 222, 1, 0, 0, 0, 1249, 1250, 5, 97, 0, 0, 1250, 1251, 5, 114, 0, 0, 1251, 1252, 5, 99, 0, 0, 1252, 1253, 5, 115, 0, 0, 1253, 1254, 5, 105, 0, 0, 1254, 1255, 5, 110, 0, 0, 1255, 1256, 5, 104, 0, 0, 1256, 224, 1, 0, 0, 0, 1257, 1258, 5, 97, 0, 0, 1258, 1259, 5, 114, 0, 0, 1259, 1260, 5, 99, 0, 0, 1260, 1261, 5, 111, 0, 0, 1261, 1262, 5, 115, 0, 0, 1262, 1263, 5, 104, 0, 0, 1263, 226, 1, 0, 0, 0, 1264, 1265, 5, 97, 0, 0, 1265, 1266, 5, 114, 0, 0, 1266, 1267, 5, 99, 0, 0, 1267, 1268, 5, 99, 0, 0, 1268, 1269, 5, 111, 0, 0, 1269, 1270, 5, 115, 0, 0, 1270, 1271, 5, 104, 0, 0, 1271, 228, 1, 0, 0, 0, 1272, 1273, 5, 97, 0, 0, 1273, 1274, 5, 114, 0, 0, 1274, 1275, 5, 116, 0, 0, 1275, 1276, 5, 97, 0, 0, 1276, 1277, 5, 110, 0, 0, 1277, 1278, 5, 104, 0, 0, 1278, 230, 1, 0, 0, 0, 1279, 1280, 5, 97, 0, 0, 1280, 1281, 5, 114, 0, 0, 1281, 1282, 5, 99, 0, 0, 1282, 1283, 5, 116, 0, 0, 1283, 1284, 5, 97, 0, 0, 1284, 1285, 5, 110, 0, 0, 1285, 1286, 5, 104, 0, 0, 1286, 232, 1, 0, 0, 0, 1287, 1288, 5, 103, 0, 0, 1288, 1289, 5, 99, 0, 0, 1289, 1290, 5, 100, 0, 0, 1290, 234, 1, 0, 0, 0, 1291, 1292, 5, 108, 0, 0, 1292, 1293, 5, 99, 0, 0, 1293, 1294, 5, 109, 0, 0, 1294, 236, 1, 0, 0, 0, 1295, 1296, 5, 102, 0, 0, 1296, 1297, 5, 108, 0, 0, 1297, 1298, 5, 111, 0, 0, 1298, 1299, 5, 111, 0, 0, 1299, 1300, 5, 114, 0, 0, 1300, 238, 1, 0, 0, 0, 1301, 1302, 5, 99, 0, 0, 1302, 1303, 5, 101, 0, 0, 1303, 1304, 5, 105, 0, 0, 1304, 1305, 5, 108, 0, 0, 1305, 240, 1, 0, 0, 0, 1306, 1307, 5, 92, 0, 0, 1307, 1308, 5, 115, 0, 0, 1308, 1309, 5, 113, 0, 0, 1309, 1310, 5, 114, 0, 0, 1310, 1311, 5, 116, 0, 0, 1311, 242, 1, 0, 0, 0, 1312, 1313, 5, 92, 0, 0, 1313, 1314, 5, 103, 0, 0, 1314, 1315, 5, 99, 0, 0, 1315, 1316, 5, 100, 0, 0, 1316, 244, 1, 0, 0, 0, 1317, 1318, 5, 92, 0, 0, 1318, 1319, 5, 108, 0, 0, 1319, 1320, 5, 99, 0, 0, 1320, 1321, 5, 109, 0, 0, 1321, 246, 1, 0, 0, 0, 1322, 1323, 5, 92, 0, 0, 1323, 1324, 5, 102, 0, 0, 1324, 1325, 5, 108, 0, 0, 1325, 1326, 5, 111, 0, 0, 1326, 1327, 5, 111, 0, 0, 1327, 1328, 5, 114, 0, 0, 1328, 248, 1, 0, 0, 0, 1329, 1330, 5, 92, 0, 0, 1330, 1331, 5, 99, 0, 0, 1331, 1332, 5, 101, 0, 0, 1332, 1333, 5, 105, 0, 0, 1333, 1334, 5, 108, 0, 0, 1334, 250, 1, 0, 0, 0, 1335, 1336, 5, 92, 0, 0, 1336, 1337, 5, 109, 0, 0, 1337, 1338, 5, 97, 0, 0, 1338, 1339, 5, 120, 0, 0, 1339, 252, 1, 0, 0, 0, 1340, 1341, 5, 92, 0, 0, 1341, 1342, 5, 109, 0, 0, 1342, 1343, 5, 105, 0, 0, 1343, 1344, 5, 110, 0, 0, 1344, 254, 1, 0, 0, 0, 1345, 1346, 5, 92, 0, 0, 1346, 1347, 5, 100, 0, 0, 1347, 1348, 5, 101, 0, 0, 1348, 1349, 5, 116, 0, 0, 1349, 256, 1, 0, 0, 0, 1350, 1351, 5, 101, 0, 0, 1351, 1352, 5, 121, 0, 0, 1352, 1353, 5, 101, 0, 0, 1353, 258, 1, 0, 0, 0, 1354, 1355, 5, 122, 0, 0, 1355, 1356, 5, 101, 0, 0, 1356, 1357, 5, 114, 0, 0, 1357, 1358, 5, 111, 0, 0, 1358, 1359, 5, 115, 0, 0, 1359, 260, 1, 0, 0, 0, 1360, 1361, 5, 111, 0, 0, 1361, 1362, 5, 110, 0, 0, 1362, 1363, 5, 101, 0, 0, 1363, 1364, 5, 115, 0, 0, 1364, 262, 1, 0, 0, 0, 1365, 1366, 5, 99, 0, 0, 1366, 1367, 5, 111, 0, 0, 1367, 1368, 5, 108, 0, 0, 1368, 1369, 5, 115, 0, 0, 1369, 264, 1, 0, 0, 0, 1370, 1371, 5, 114, 0, 0, 1371, 1372, 5, 111, 0, 0, 1372, 1373, 5, 119, 0, 0, 1373, 1374, 5, 115, 0, 0, 1374, 266, 1, 0, 0, 0, 1375, 1376, 5, 100, 0, 0, 1376, 1377, 5, 105, 0, 0, 1377, 1378, 5, 97, 0, 0, 1378, 1379, 5, 103, 0, 0, 1379, 268, 1, 0, 0, 0, 1380, 1381, 5, 110, 0, 0, 1381, 1382, 5, 111, 0, 0, 1382, 1383, 5, 114, 0, 0, 1383, 1384, 5, 109, 0, 0, 1384, 270, 1, 0, 0, 0, 1385, 1386, 5, 114, 0, 0, 1386, 1387, 5, 97, 0, 0, 1387, 1388, 5, 110, 0, 0, 1388, 1389, 5, 107, 0, 0, 1389, 272, 1, 0, 0, 0, 1390, 1391, 5, 116, 0, 0, 1391, 1392, 5, 114, 0, 0, 1392, 1393, 5, 97, 0, 0, 1393, 1394, 5, 99, 0, 0, 1394, 1398, 5, 101, 0, 0, 1395, 1396, 5, 116, 0, 0, 1396, 1398, 5, 114, 0, 0, 1397, 1390, 1, 0, 0, 0, 1397, 1395, 1, 0, 0, 0, 1398, 274, 1, 0, 0, 0, 1399, 1400, 5, 114, 0, 0, 1400, 1401, 5, 114, 0, 0, 1401, 1402, 5, 101, 0, 0, 1402, 1403, 5, 102, 0, 0, 1403, 276, 1, 0, 0, 0, 1404, 1405, 5, 104, 0, 0, 1405, 1406, 5, 115, 0, 0, 1406, 1407, 5, 116, 0, 0, 1407, 1408, 5, 97, 0, 0, 1408, 1409, 5, 99, 0, 0, 1409, 1410, 5, 107, 0, 0, 1410, 278, 1, 0, 0, 0, 1411, 1412, 5, 118, 0, 0, 1412, 1413, 5, 115, 0, 0, 1413, 1414, 5, 116, 0, 0, 1414, 1415, 5, 97, 0, 0, 1415, 1416, 5, 99, 0, 0, 1416, 1417, 5, 107, 0, 0, 1417, 280, 1, 0, 0, 0, 1418, 1419, 5, 111, 0, 0, 1419, 1420, 5, 114, 0, 0, 1420, 1421, 5, 116, 0, 0, 1421, 1451, 5, 104, 0, 0, 1422, 1423, 5, 111, 0, 0, 1423, 1424, 5, 114, 0, 0, 1424, 1425, 5, 116, 0, 0, 1425, 1426, 5, 104, 0, 0, 1426, 1451, 5, 111, 0, 0, 1427, 1428, 5, 111, 0, 0, 1428, 1429, 5, 114, 0, 0, 1429, 1430, 5, 116, 0, 0, 1430, 1431, 5, 104, 0, 0, 1431, 1432, 5, 111, 0, 0, 1432, 1433, 5, 103, 0, 0, 1433, 1434, 5, 111, 0, 0, 1434, 1435, 5, 110, 0, 0, 1435, 1436, 5, 97, 0, 0, 1436, 1451, 5, 108, 0, 0, 1437, 1438, 5, 111, 0, 0, 1438, 1439, 5, 114, 0, 0, 1439, 1440, 5, 116, 0, 0, 1440, 1441, 5, 104, 0, 0, 1441, 1442, 5, 111, 0, 0, 1442, 1443, 5, 103, 0, 0, 1443, 1444, 5, 111, 0, 0, 1444, 1445, 5, 110, 0, 0, 1445, 1446, 5, 97, 0, 0, 1446, 1447, 5, 108, 0, 0, 1447, 1448, 5, 105, 0, 0, 1448, 1449, 5, 122, 0, 0, 1449, 1451, 5, 101, 0, 0, 1450, 1418, 1, 0, 0, 0, 1450, 1422, 1, 0, 0, 0, 1450, 1427, 1, 0, 0, 0, 1450, 1437, 1, 0, 0, 0, 1451, 282, 1, 0, 0, 0, 1452, 1453, 5, 110, 0, 0, 1453, 1454, 5, 117, 0, 0, 1454, 1455, 5, 108, 0, 0, 1455, 1456, 5, 108, 0, 0, 1456, 1457, 5, 115, 0, 0, 1457, 1458, 5, 112, 0, 0, 1458, 1459, 5, 97, 0, 0, 1459, 1460, 5, 99, 0, 0, 1460, 1461, 5, 101, 0, 0, 1461, 284, 1, 0, 0, 0, 1462, 1463, 5, 101, 0, 0, 1463, 1464, 5, 105, 0, 0, 1464, 1482, 5, 103, 0, 0, 1465, 1466, 5, 101, 0, 0, 1466, 1467, 5, 105, 0, 0, 1467, 1468, 5, 103, 0, 0, 1468, 1469, 5, 101, 0, 0, 1469, 1482, 5, 110, 0, 0, 1470, 1471, 5, 100, 0, 0, 1471, 1472, 5, 105, 0, 0, 1472, 1473, 5, 97, 0, 0, 1473, 1474, 5, 103, 0, 0, 1474, 1475, 5, 111, 0, 0, 1475, 1476, 5, 110, 0, 0, 1476, 1477, 5, 97, 0, 0, 1477, 1478, 5, 108, 0, 0, 1478, 1479, 5, 105, 0, 0, 1479, 1480, 5, 122, 0, 0, 1480, 1482, 5, 101, 0, 0, 1481, 1462, 1, 0, 0, 0, 1481, 1465, 1, 0, 0, 0, 1481, 1470, 1, 0, 0, 0, 1482, 286, 1, 0, 0, 0, 1483, 1484, 5, 101, 0, 0, 1484, 1485, 5, 105, 0, 0, 1485, 1486, 5, 103, 0, 0, 1486, 1487, 5, 101, 0, 0, 1487, 1488, 5, 110, 0, 0, 1488, 1489, 5, 118, 0, 0, 1489, 1490, 5, 97, 0, 0, 1490, 1491, 5, 108, 0, 0, 1491, 1504, 5, 115, 0, 0, 1492, 1493, 5, 101, 0, 0, 1493, 1494, 5, 105, 0, 0, 1494, 1495, 5, 103, 0, 0, 1495, 1496, 5, 101, 0, 0, 1496, 1497, 5, 110, 0, 0, 1497, 1498, 5, 118, 0, 0, 1498, 1499, 5, 97, 0, 0, 1499, 1500, 5, 108, 0, 0, 1500, 1501, 5, 117, 0, 0, 1501, 1502, 5, 101, 0, 0, 1502, 1504, 5, 115, 0, 0, 1503, 1483, 1, 0, 0, 0, 1503, 1492, 1, 0, 0, 0, 1504, 288, 1, 0, 0, 0, 1505, 1506, 5, 101, 0, 0, 1506, 1507, 5, 105, 0, 0, 1507, 1508, 5, 103, 0, 0, 1508, 1509, 5, 101, 0, 0, 1509, 1510, 5, 110, 0, 0, 1510, 1511, 5, 118, 0, 0, 1511, 1512, 5, 101, 0, 0, 1512, 1513, 5, 99, 0, 0, 1513, 1514, 5, 116, 0, 0, 1514, 1528, 5, 115, 0, 0, 1515, 1516, 5, 101, 0, 0, 1516, 1517, 5, 105, 0, 0, 1517, 1518, 5, 103, 0, 0, 1518, 1519, 5, 101, 0, 0, 1519, 1520, 5, 110, 0, 0, 1520, 1521, 5, 118, 0, 0, 1521, 1522, 5, 101, 0, 0, 1522, 1523, 5, 99, 0, 0, 1523, 1524, 5, 116, 0, 0, 1524, 1525, 5, 111, 0, 0, 1525, 1526, 5, 114, 0, 0, 1526, 1528, 5, 115, 0, 0, 1527, 1505, 1, 0, 0, 0, 1527, 1515, 1, 0, 0, 0, 1528, 290, 1, 0, 0, 0, 1529, 1530, 5, 115, 0, 0, 1530, 1531, 5, 118, 0, 0, 1531, 1536, 5, 100, 0, 0, 1532, 1533, 5, 83, 0, 0, 1533, 1534, 5, 86, 0, 0, 1534, 1536, 5, 68, 0, 0, 1535, 1529, 1, 0, 0, 0, 1535, 1532, 1, 0, 0, 0, 1536, 292, 1, 0, 0, 0, 1537, 1538, 5, 92, 0, 0, 1538, 1539, 5, 116, 0, 0, 1539, 1540, 5, 105, 0, 0, 1540, 1541, 5, 109, 0, 0, 1541, 1542, 5, 101, 0, 0, 1542, 1543, 5, 115, 0, 0, 1543, 294, 1, 0, 0, 0, 1544, 1545, 5, 92, 0, 0, 1545, 1546, 5, 99, 0, 0, 1546, 1547, 5, 100, 0, 0, 1547, 1548, 5, 111, 0, 0, 1548, 1549, 5, 116, 0, 0, 1549, 296, 1, 0, 0, 0, 1550, 1551, 5, 92, 0, 0, 1551, 1552, 5, 100, 0, 0, 1552, 1553, 5, 105, 0, 0, 1553, 1554, 5, 118, 0, 0, 1554, 298, 1, 0, 0, 0, 1555, 1556, 5, 92, 0, 0, 1556, 1557, 5, 102, 0, 0, 1557, 1558, 5, 114, 0, 0, 1558, 1559, 5, 97, 0, 0, 1559, 1560, 5, 99, 0, 0, 1560, 300, 1, 0, 0, 0, 1561, 1562, 5, 92, 0, 0, 1562, 1563, 5, 98, 0, 0, 1563, 1564, 5, 105, 0, 0, 1564, 1565, 5, 110, 0, 0, 1565, 1566, 5, 111, 0, 0, 1566, 1582, 5, 109, 0, 0, 1567, 1568, 5, 92, 0, 0, 1568, 1569, 5, 116, 0, 0, 1569, 1570, 5, 98, 0, 0, 1570, 1571, 5, 105, 0, 0, 1571, 1572, 5, 110, 0, 0, 1572, 1573, 5, 111, 0, 0, 1573, 1582, 5, 109, 0, 0, 1574, 1575, 5, 92, 0, 0, 1575, 1576, 5, 100, 0, 0, 1576, 1577, 5, 98, 0, 0, 1577, 1578, 5, 105, 0, 0, 1578, 1579, 5, 110, 0, 0, 1579, 1580, 5, 111, 0, 0, 1580, 1582, 5, 109, 0, 0, 1581, 1561, 1, 0, 0, 0, 1581, 1567, 1, 0, 0, 0, 1581, 1574, 1, 0, 0, 0, 1582, 302, 1, 0, 0, 0, 1583, 1584, 5, 92, 0, 0, 1584, 1585, 5, 99, 0, 0, 1585, 1586, 5, 104, 0, 0, 1586, 1587, 5, 111, 0, 0, 1587, 1588, 5, 111, 0, 0, 1588, 1589, 5, 115, 0, 0, 1589, 1590, 5, 101, 0, 0, 1590, 304, 1, 0, 0, 0, 1591, 1592, 5, 92, 0, 0, 1592, 1593, 5, 109, 0, 0, 1593, 1594, 5, 111, 0, 0, 1594, 1595, 5, 100, 0, 0, 1595, 306, 1, 0, 0, 0, 1596, 1597, 5, 92, 0, 0, 1597, 1598, 5, 109, 0, 0, 1598, 1599, 5, 97, 0, 0, 1599, 1600, 5, 116, 0, 0, 1600, 1601, 5, 104, 0, 0, 1601, 1602, 5, 105, 0, 0, 1602, 1603, 5, 116, 0, 0, 1603, 308, 1, 0, 0, 0, 1604, 1605, 5, 92, 0, 0, 1605, 1606, 5, 111, 0, 0, 1606, 1607, 5, 112, 0, 0, 1607, 1608, 5, 101, 0, 0, 1608, 1609, 5, 114, 0, 0, 1609, 1610, 5, 97, 0, 0, 1610, 1611, 5, 116, 0, 0, 1611, 1612, 5, 111, 0, 0, 1612, 1613, 5, 114, 0, 0, 1613, 1614, 5, 110, 0, 0, 1614, 1615, 5, 97, 0, 0, 1615, 1616, 5, 109, 0, 0, 1616, 1617, 5, 101, 0, 0, 1617, 310, 1, 0, 0, 0, 1618, 1619, 5, 109, 0, 0, 1619, 1620, 5, 97, 0, 0, 1620, 1621, 5, 116, 0, 0, 1621, 1622, 5, 114, 0, 0, 1622, 1623, 5, 105, 0, 0, 1623, 1624, 5, 120, 0, 0, 1624, 312, 1, 0, 0, 0, 1625, 1626, 5, 112, 0, 0, 1626, 1627, 5, 109, 0, 0, 1627, 1628, 5, 97, 0, 0, 1628, 1629, 5, 116, 0, 0, 1629, 1630, 5, 114, 0, 0, 1630, 1631, 5, 105, 0, 0, 1631, 1632, 5, 120, 0, 0, 1632, 314, 1, 0, 0, 0, 1633, 1634, 5, 98, 0, 0, 1634, 1635, 5, 109, 0, 0, 1635, 1636, 5, 97, 0, 0, 1636, 1637, 5, 116, 0, 0, 1637, 1638, 5, 114, 0, 0, 1638, 1639, 5, 105, 0, 0, 1639, 1640, 5, 120, 0, 0, 1640, 316, 1, 0, 0, 0, 1641, 1642, 5, 118, 0, 0, 1642, 1643, 5, 109, 0, 0, 1643, 1644, 5, 97, 0, 0, 1644, 1645, 5, 116, 0, 0, 1645, 1646, 5, 114, 0, 0, 1646, 1647, 5, 105, 0, 0, 1647, 1648, 5, 120, 0, 0, 1648, 318, 1, 0, 0, 0, 1649, 1653, 3, 311, 155, 0, 1650, 1653, 3, 313, 156, 0, 1651, 1653, 3, 315, 157, 0, 1652, 1649, 1, 0, 0, 0, 1652, 1650, 1, 0, 0, 0, 1652, 1651, 1, 0, 0, 0, 1653, 320, 1, 0, 0, 0, 1654, 1655, 5, 92, 0, 0, 1655, 1656, 5, 98, 0, 0, 1656, 1657, 5, 101, 0, 0, 1657, 1658, 5, 103, 0, 0, 1658, 1659, 5, 105, 0, 0, 1659, 1660, 5, 110, 0, 0, 1660, 1661, 1, 0, 0, 0, 1661, 1662, 3, 109, 54, 0, 1662, 1663, 3, 319, 159, 0, 1663, 1664, 3, 111, 55, 0, 1664, 322, 1, 0, 0, 0, 1665, 1666, 5, 92, 0, 0, 1666, 1667, 5, 101, 0, 0, 1667, 1668, 5, 110, 0, 0, 1668, 1669, 5, 100, 0, 0, 1669, 1670, 1, 0, 0, 0, 1670, 1671, 3, 109, 54, 0, 1671, 1672, 3, 319, 159, 0, 1672, 1673, 3, 111, 55, 0, 1673, 324, 1, 0, 0, 0, 1674, 1675, 5, 92, 0, 0, 1675, 1676, 5, 98, 0, 0, 1676, 1677, 5, 101, 0, 0, 1677, 1678, 5, 103, 0, 0, 1678, 1679, 5, 105, 0, 0, 1679, 1680, 5, 110, 0, 0, 1680, 1681, 1, 0, 0, 0, 1681, 1682, 3, 109, 54, 0, 1682, 1683, 3, 317, 158, 0, 1683, 1684, 3, 111, 55, 0, 1684, 326, 1, 0, 0, 0, 1685, 1686, 5, 92, 0, 0, 1686, 1687, 5, 101, 0, 0, 1687, 1688, 5, 110, 0, 0, 1688, 1689, 5, 100, 0, 0, 1689, 1690, 1, 0, 0, 0, 1690, 1691, 3, 109, 54, 0, 1691, 1692, 3, 317, 158, 0, 1692, 1693, 3, 111, 55, 0, 1693, 328, 1, 0, 0, 0, 1694, 1695, 5, 38, 0, 0, 1695, 330, 1, 0, 0, 0, 1696, 1697, 5, 92, 0, 0, 1697, 1698, 5, 92, 0, 0, 1698, 332, 1, 0, 0, 0, 1699, 1700, 5, 95, 0, 0, 1700, 334, 1, 0, 0, 0, 1701, 1702, 5, 94, 0, 0, 1702, 336, 1, 0, 0, 0, 1703, 1704, 5, 58, 0, 0, 1704, 338, 1, 0, 0, 0, 1705, 1706, 5, 59, 0, 0, 1706, 340, 1, 0, 0, 0, 1707, 1708, 5, 44, 0, 0, 1708, 342, 1, 0, 0, 0, 1709, 1710, 5, 46, 0, 0, 1710, 344, 1, 0, 0, 0, 1711, 1712, 7, 0, 0, 0, 1712, 346, 1, 0, 0, 0, 1713, 1717, 5, 100, 0, 0, 1714, 1716, 3, 345, 172, 0, 1715, 1714, 1, 0, 0, 0, 1716, 1719, 1, 0, 0, 0, 1717, 1718, 1, 0, 0, 0, 1717, 1715, 1, 0, 0, 0, 1718, 1727, 1, 0, 0, 0, 1719, 1717, 1, 0, 0, 0, 1720, 1728, 7, 1, 0, 0, 1721, 1723, 5, 92, 0, 0, 1722, 1724, 7, 1, 0, 0, 1723, 1722, 1, 0, 0, 0, 1724, 1725, 1, 0, 0, 0, 1725, 1723, 1, 0, 0, 0, 1725, 1726, 1, 0, 0, 0, 1726, 1728, 1, 0, 0, 0, 1727, 1720, 1, 0, 0, 0, 1727, 1721, 1, 0, 0, 0, 1728, 348, 1, 0, 0, 0, 1729, 1744, 5, 101, 0, 0, 1730, 1731, 5, 92, 0, 0, 1731, 1732, 5, 101, 0, 0, 1732, 1733, 5, 120, 0, 0, 1733, 1734, 5, 112, 0, 0, 1734, 1735, 5, 111, 0, 0, 1735, 1736, 5, 110, 0, 0, 1736, 1737, 5, 101, 0, 0, 1737, 1738, 5, 110, 0, 0, 1738, 1739, 5, 116, 0, 0, 1739, 1740, 5, 105, 0, 0, 1740, 1741, 5, 97, 0, 0, 1741, 1742, 5, 108, 0, 0, 1742, 1744, 5, 69, 0, 0, 1743, 1729, 1, 0, 0, 0, 1743, 1730, 1, 0, 0, 0, 1744, 350, 1, 0, 0, 0, 1745, 1746, 5, 69, 0, 0, 1746, 352, 1, 0, 0, 0, 1747, 1748, 7, 2, 0, 0, 1748, 354, 1, 0, 0, 0, 1749, 1750, 7, 1, 0, 0, 1750, 356, 1, 0, 0, 0, 1751, 1752, 7, 3, 0, 0, 1752, 358, 1, 0, 0, 0, 1753, 1754, 5, 92, 0, 0, 1754, 1755, 5, 120, 0, 0, 1755, 1756, 5, 114, 0, 0, 1756, 1757, 5, 105, 0, 0, 1757, 1758, 5, 103, 0, 0, 1758, 1759, 5, 104, 0, 0, 1759, 1760, 5, 116, 0, 0, 1760, 1761, 5, 97, 0, 0, 1761, 1762, 5, 114, 0, 0, 1762, 1763, 5, 114, 0, 0, 1763, 1764, 5, 111, 0, 0, 1764, 1778, 5, 119, 0, 0, 1765, 1766, 5, 92, 0, 0, 1766, 1767, 5, 120, 0, 0, 1767, 1768, 5, 82, 0, 0, 1768, 1769, 5, 105, 0, 0, 1769, 1770, 5, 103, 0, 0, 1770, 1771, 5, 104, 0, 0, 1771, 1772, 5, 116, 0, 0, 1772, 1773, 5, 97, 0, 0, 1773, 1774, 5, 114, 0, 0, 1774, 1775, 5, 114, 0, 0, 1775, 1776, 5, 111, 0, 0, 1776, 1778, 5, 119, 0, 0, 1777, 1753, 1, 0, 0, 0, 1777, 1765, 1, 0, 0, 0, 1778, 360, 1, 0, 0, 0, 1779, 1780, 5, 60, 0, 0, 1780, 1781, 5, 45, 0, 0, 1781, 1816, 5, 62, 0, 0, 1782, 1783, 5, 60, 0, 0, 1783, 1784, 5, 61, 0, 0, 1784, 1816, 5, 62, 0, 0, 1785, 1786, 5, 92, 0, 0, 1786, 1787, 5, 108, 0, 0, 1787, 1788, 5, 101, 0, 0, 1788, 1789, 5, 102, 0, 0, 1789, 1790, 5, 116, 0, 0, 1790, 1791, 5, 114, 0, 0, 1791, 1792, 5, 105, 0, 0, 1792, 1793, 5, 103, 0, 0, 1793, 1794, 5, 104, 0, 0, 1794, 1795, 5, 116, 0, 0, 1795, 1796, 5, 97, 0, 0, 1796, 1797, 5, 114, 0, 0, 1797, 1798, 5, 114, 0, 0, 1798, 1799, 5, 111, 0, 0, 1799, 1816, 5, 119, 0, 0, 1800, 1801, 5, 92, 0, 0, 1801, 1802, 5, 76, 0, 0, 1802, 1803, 5, 101, 0, 0, 1803, 1804, 5, 102, 0, 0, 1804, 1805, 5, 116, 0, 0, 1805, 1806, 5, 114, 0, 0, 1806, 1807, 5, 105, 0, 0, 1807, 1808, 5, 103, 0, 0, 1808, 1809, 5, 104, 0, 0, 1809, 1810, 5, 116, 0, 0, 1810, 1811, 5, 97, 0, 0, 1811, 1812, 5, 114, 0, 0, 1812, 1813, 5, 114, 0, 0, 1813, 1814, 5, 111, 0, 0, 1814, 1816, 5, 119, 0, 0, 1815, 1779, 1, 0, 0, 0, 1815, 1782, 1, 0, 0, 0, 1815, 1785, 1, 0, 0, 0, 1815, 1800, 1, 0, 0, 0, 1816, 362, 1, 0, 0, 0, 1817, 1819, 3, 357, 178, 0, 1818, 1817, 1, 0, 0, 0, 1819, 1820, 1, 0, 0, 0, 1820, 1818, 1, 0, 0, 0, 1820, 1821, 1, 0, 0, 0, 1821, 1829, 1, 0, 0, 0, 1822, 1823, 3, 341, 170, 0, 1823, 1824, 3, 357, 178, 0, 1824, 1825, 3, 357, 178, 0, 1825, 1826, 3, 357, 178, 0, 1826, 1828, 1, 0, 0, 0, 1827, 1822, 1, 0, 0, 0, 1828, 1831, 1, 0, 0, 0, 1829, 1827, 1, 0, 0, 0, 1829, 1830, 1, 0, 0, 0, 1830, 1855, 1, 0, 0, 0, 1831, 1829, 1, 0, 0, 0, 1832, 1834, 3, 357, 178, 0, 1833, 1832, 1, 0, 0, 0, 1834, 1837, 1, 0, 0, 0, 1835, 1833, 1, 0, 0, 0, 1835, 1836, 1, 0, 0, 0, 1836, 1845, 1, 0, 0, 0, 1837, 1835, 1, 0, 0, 0, 1838, 1839, 3, 341, 170, 0, 1839, 1840, 3, 357, 178, 0, 1840, 1841, 3, 357, 178, 0, 1841, 1842, 3, 357, 178, 0, 1842, 1844, 1, 0, 0, 0, 1843, 1838, 1, 0, 0, 0, 1844, 1847, 1, 0, 0, 0, 1845, 1843, 1, 0, 0, 0, 1845, 1846, 1, 0, 0, 0, 1846, 1848, 1, 0, 0, 0, 1847, 1845, 1, 0, 0, 0, 1848, 1850, 3, 343, 171, 0, 1849, 1851, 3, 357, 178, 0, 1850, 1849, 1, 0, 0, 0, 1851, 1852, 1, 0, 0, 0, 1852, 1850, 1, 0, 0, 0, 1852, 1853, 1, 0, 0, 0, 1853, 1855, 1, 0, 0, 0, 1854, 1818, 1, 0, 0, 0, 1854, 1835, 1, 0, 0, 0, 1855, 364, 1, 0, 0, 0, 1856, 1857, 3, 363, 181, 0, 1857, 1860, 3, 351, 175, 0, 1858, 1861, 3, 95, 47, 0, 1859, 1861, 3, 93, 46, 0, 1860, 1858, 1, 0, 0, 0, 1860, 1859, 1, 0, 0, 0, 1860, 1861, 1, 0, 0, 0, 1861, 1863, 1, 0, 0, 0, 1862, 1864, 3, 357, 178, 0, 1863, 1862, 1, 0, 0, 0, 1864, 1865, 1, 0, 0, 0, 1865, 1863, 1, 0, 0, 0, 1865, 1866, 1, 0, 0, 0, 1866, 366, 1, 0, 0, 0, 1867, 1868, 5, 92, 0, 0, 1868, 1869, 5, 105, 0, 0, 1869, 1870, 5, 110, 0, 0, 1870, 368, 1, 0, 0, 0, 1871, 1872, 5, 61, 0, 0, 1872, 370, 1, 0, 0, 0, 1873, 1874, 5, 61, 0, 0, 1874, 1882, 5, 61, 0, 0, 1875, 1876, 5, 92, 0, 0, 1876, 1877, 5, 101, 0, 0, 1877, 1878, 5, 113, 0, 0, 1878, 1879, 5, 117, 0, 0, 1879, 1880, 5, 105, 0, 0, 1880, 1882, 5, 118, 0, 0, 1881, 1873, 1, 0, 0, 0, 1881, 1875, 1, 0, 0, 0, 1882, 372, 1, 0, 0, 0, 1883, 1884, 5, 60, 0, 0, 1884, 374, 1, 0, 0, 0, 1885, 1886, 5, 92, 0, 0, 1886, 1887, 5, 108, 0, 0, 1887, 1888, 5, 101, 0, 0, 1888, 1902, 5, 113, 0, 0, 1889, 1890, 5, 92, 0, 0, 1890, 1891, 5, 108, 0, 0, 1891, 1902, 5, 101, 0, 0, 1892, 1893, 5, 92, 0, 0, 1893, 1894, 5, 108, 0, 0, 1894, 1895, 5, 101, 0, 0, 1895, 1896, 5, 113, 0, 0, 1896, 1897, 5, 115, 0, 0, 1897, 1898, 5, 108, 0, 0, 1898, 1899, 5, 97, 0, 0, 1899, 1900, 5, 110, 0, 0, 1900, 1902, 5, 116, 0, 0, 1901, 1885, 1, 0, 0, 0, 1901, 1889, 1, 0, 0, 0, 1901, 1892, 1, 0, 0, 0, 1902, 376, 1, 0, 0, 0, 1903, 1904, 5, 62, 0, 0, 1904, 378, 1, 0, 0, 0, 1905, 1906, 5, 92, 0, 0, 1906, 1907, 5, 103, 0, 0, 1907, 1908, 5, 101, 0, 0, 1908, 1922, 5, 113, 0, 0, 1909, 1910, 5, 92, 0, 0, 1910, 1911, 5, 103, 0, 0, 1911, 1922, 5, 101, 0, 0, 1912, 1913, 5, 92, 0, 0, 1913, 1914, 5, 103, 0, 0, 1914, 1915, 5, 101, 0, 0, 1915, 1916, 5, 113, 0, 0, 1916, 1917, 5, 115, 0, 0, 1917, 1918, 5, 108, 0, 0, 1918, 1919, 5, 97, 0, 0, 1919, 1920, 5, 110, 0, 0, 1920, 1922, 5, 116, 0, 0, 1921, 1905, 1, 0, 0, 0, 1921, 1909, 1, 0, 0, 0, 1921, 1912, 1, 0, 0, 0, 1922, 380, 1, 0, 0, 0, 1923, 1924, 5, 33, 0, 0, 1924, 1946, 5, 61, 0, 0, 1925, 1926, 5, 33, 0, 0, 1926, 1927, 5, 61, 0, 0, 1927, 1946, 5, 61, 0, 0, 1928, 1929, 5, 92, 0, 0, 1929, 1930, 5, 110, 0, 0, 1930, 1946, 5, 101, 0, 0, 1931, 1932, 5, 92, 0, 0, 1932, 1933, 5, 110, 0, 0, 1933, 1934, 5, 101, 0, 0, 1934, 1946, 5, 113, 0, 0, 1935, 1936, 5, 92, 0, 0, 1936, 1937, 5, 110, 0, 0, 1937, 1938, 5, 111, 0, 0, 1938, 1939, 5, 116, 0, 0, 1939, 1940, 5, 92, 0, 0, 1940, 1941, 5, 101, 0, 0, 1941, 1942, 5, 113, 0, 0, 1942, 1943, 5, 117, 0, 0, 1943, 1944, 5, 105, 0, 0, 1944, 1946, 5, 118, 0, 0, 1945, 1923, 1, 0, 0, 0, 1945, 1925, 1, 0, 0, 0, 1945, 1928, 1, 0, 0, 0, 1945, 1931, 1, 0, 0, 0, 1945, 1935, 1, 0, 0, 0, 1946, 382, 1, 0, 0, 0, 1947, 1948, 5, 33, 0, 0, 1948, 384, 1, 0, 0, 0, 1949, 1950, 5, 92, 0, 0, 1950, 1951, 5, 37, 0, 0, 1951, 386, 1, 0, 0, 0, 1952, 1953, 3, 363, 181, 0, 1953, 1954, 3, 385, 192, 0, 1954, 388, 1, 0, 0, 0, 1955, 1956, 5, 92, 0, 0, 1956, 1957, 5, 99, 0, 0, 1957, 1958, 5, 104, 0, 0, 1958, 1959, 5, 97, 0, 0, 1959, 1960, 5, 114, 0, 0, 1960, 1961, 5, 34, 0, 0, 1961, 1962, 5, 48, 0, 0, 1962, 1963, 5, 48, 0, 0, 1963, 1964, 5, 48, 0, 0, 1964, 1965, 5, 51, 0, 0, 1965, 1966, 5, 57, 0, 0, 1966, 2341, 5, 49, 0, 0, 1967, 1968, 5, 92, 0, 0, 1968, 1969, 5, 97, 0, 0, 1969, 1970, 5, 108, 0, 0, 1970, 1971, 5, 112, 0, 0, 1971, 1972, 5, 104, 0, 0, 1972, 2341, 5, 97, 0, 0, 1973, 1974, 5, 92, 0, 0, 1974, 1975, 5, 99, 0, 0, 1975, 1976, 5, 104, 0, 0, 1976, 1977, 5, 97, 0, 0, 1977, 1978, 5, 114, 0, 0, 1978, 1979, 5, 34, 0, 0, 1979, 1980, 5, 48, 0, 0, 1980, 1981, 5, 48, 0, 0, 1981, 1982, 5, 48, 0, 0, 1982, 1983, 5, 51, 0, 0, 1983, 1984, 5, 57, 0, 0, 1984, 2341, 5, 50, 0, 0, 1985, 1986, 5, 92, 0, 0, 1986, 1987, 5, 98, 0, 0, 1987, 1988, 5, 101, 0, 0, 1988, 1989, 5, 116, 0, 0, 1989, 2341, 5, 97, 0, 0, 1990, 1991, 5, 92, 0, 0, 1991, 1992, 5, 71, 0, 0, 1992, 1993, 5, 97, 0, 0, 1993, 1994, 5, 109, 0, 0, 1994, 1995, 5, 109, 0, 0, 1995, 2341, 5, 97, 0, 0, 1996, 1997, 5, 92, 0, 0, 1997, 1998, 5, 103, 0, 0, 1998, 1999, 5, 97, 0, 0, 1999, 2000, 5, 109, 0, 0, 2000, 2001, 5, 109, 0, 0, 2001, 2341, 5, 97, 0, 0, 2002, 2003, 5, 92, 0, 0, 2003, 2004, 5, 68, 0, 0, 2004, 2005, 5, 101, 0, 0, 2005, 2006, 5, 108, 0, 0, 2006, 2007, 5, 116, 0, 0, 2007, 2341, 5, 97, 0, 0, 2008, 2009, 5, 92, 0, 0, 2009, 2010, 5, 100, 0, 0, 2010, 2011, 5, 101, 0, 0, 2011, 2012, 5, 108, 0, 0, 2012, 2013, 5, 116, 0, 0, 2013, 2341, 5, 97, 0, 0, 2014, 2015, 5, 92, 0, 0, 2015, 2016, 5, 99, 0, 0, 2016, 2017, 5, 104, 0, 0, 2017, 2018, 5, 97, 0, 0, 2018, 2019, 5, 114, 0, 0, 2019, 2020, 5, 34, 0, 0, 2020, 2021, 5, 48, 0, 0, 2021, 2022, 5, 48, 0, 0, 2022, 2023, 5, 48, 0, 0, 2023, 2024, 5, 49, 0, 0, 2024, 2025, 5, 57, 0, 0, 2025, 2341, 5, 48, 0, 0, 2026, 2027, 5, 92, 0, 0, 2027, 2028, 5, 101, 0, 0, 2028, 2029, 5, 112, 0, 0, 2029, 2030, 5, 115, 0, 0, 2030, 2031, 5, 105, 0, 0, 2031, 2032, 5, 108, 0, 0, 2032, 2033, 5, 111, 0, 0, 2033, 2341, 5, 110, 0, 0, 2034, 2035, 5, 92, 0, 0, 2035, 2036, 5, 118, 0, 0, 2036, 2037, 5, 97, 0, 0, 2037, 2038, 5, 114, 0, 0, 2038, 2039, 5, 101, 0, 0, 2039, 2040, 5, 112, 0, 0, 2040, 2041, 5, 115, 0, 0, 2041, 2042, 5, 105, 0, 0, 2042, 2043, 5, 108, 0, 0, 2043, 2044, 5, 111, 0, 0, 2044, 2341, 5, 110, 0, 0, 2045, 2046, 5, 92, 0, 0, 2046, 2047, 5, 99, 0, 0, 2047, 2048, 5, 104, 0, 0, 2048, 2049, 5, 97, 0, 0, 2049, 2050, 5, 114, 0, 0, 2050, 2051, 5, 34, 0, 0, 2051, 2052, 5, 48, 0, 0, 2052, 2053, 5, 48, 0, 0, 2053, 2054, 5, 48, 0, 0, 2054, 2055, 5, 51, 0, 0, 2055, 2056, 5, 57, 0, 0, 2056, 2341, 5, 54, 0, 0, 2057, 2058, 5, 92, 0, 0, 2058, 2059, 5, 122, 0, 0, 2059, 2060, 5, 101, 0, 0, 2060, 2061, 5, 116, 0, 0, 2061, 2341, 5, 97, 0, 0, 2062, 2063, 5, 92, 0, 0, 2063, 2064, 5, 99, 0, 0, 2064, 2065, 5, 104, 0, 0, 2065, 2066, 5, 97, 0, 0, 2066, 2067, 5, 114, 0, 0, 2067, 2068, 5, 34, 0, 0, 2068, 2069, 5, 48, 0, 0, 2069, 2070, 5, 48, 0, 0, 2070, 2071, 5, 48, 0, 0, 2071, 2072, 5, 51, 0, 0, 2072, 2073, 5, 57, 0, 0, 2073, 2341, 5, 55, 0, 0, 2074, 2075, 5, 92, 0, 0, 2075, 2076, 5, 101, 0, 0, 2076, 2077, 5, 116, 0, 0, 2077, 2341, 5, 97, 0, 0, 2078, 2079, 5, 92, 0, 0, 2079, 2080, 5, 84, 0, 0, 2080, 2081, 5, 104, 0, 0, 2081, 2082, 5, 101, 0, 0, 2082, 2083, 5, 116, 0, 0, 2083, 2341, 5, 97, 0, 0, 2084, 2085, 5, 92, 0, 0, 2085, 2086, 5, 116, 0, 0, 2086, 2087, 5, 104, 0, 0, 2087, 2088, 5, 101, 0, 0, 2088, 2089, 5, 116, 0, 0, 2089, 2341, 5, 97, 0, 0, 2090, 2091, 5, 92, 0, 0, 2091, 2092, 5, 118, 0, 0, 2092, 2093, 5, 97, 0, 0, 2093, 2094, 5, 114, 0, 0, 2094, 2095, 5, 116, 0, 0, 2095, 2096, 5, 104, 0, 0, 2096, 2097, 5, 101, 0, 0, 2097, 2098, 5, 116, 0, 0, 2098, 2341, 5, 97, 0, 0, 2099, 2100, 5, 92, 0, 0, 2100, 2101, 5, 99, 0, 0, 2101, 2102, 5, 104, 0, 0, 2102, 2103, 5, 97, 0, 0, 2103, 2104, 5, 114, 0, 0, 2104, 2105, 5, 34, 0, 0, 2105, 2106, 5, 48, 0, 0, 2106, 2107, 5, 48, 0, 0, 2107, 2108, 5, 48, 0, 0, 2108, 2109, 5, 51, 0, 0, 2109, 2110, 5, 57, 0, 0, 2110, 2341, 5, 57, 0, 0, 2111, 2112, 5, 92, 0, 0, 2112, 2113, 5, 105, 0, 0, 2113, 2114, 5, 111, 0, 0, 2114, 2115, 5, 116, 0, 0, 2115, 2341, 5, 97, 0, 0, 2116, 2117, 5, 92, 0, 0, 2117, 2118, 5, 99, 0, 0, 2118, 2119, 5, 104, 0, 0, 2119, 2120, 5, 97, 0, 0, 2120, 2121, 5, 114, 0, 0, 2121, 2122, 5, 34, 0, 0, 2122, 2123, 5, 48, 0, 0, 2123, 2124, 5, 48, 0, 0, 2124, 2125, 5, 48, 0, 0, 2125, 2126, 5, 51, 0, 0, 2126, 2127, 5, 57, 0, 0, 2127, 2341, 5, 65, 0, 0, 2128, 2129, 5, 92, 0, 0, 2129, 2130, 5, 107, 0, 0, 2130, 2131, 5, 97, 0, 0, 2131, 2132, 5, 112, 0, 0, 2132, 2133, 5, 112, 0, 0, 2133, 2341, 5, 97, 0, 0, 2134, 2135, 5, 92, 0, 0, 2135, 2136, 5, 76, 0, 0, 2136, 2137, 5, 97, 0, 0, 2137, 2138, 5, 109, 0, 0, 2138, 2139, 5, 98, 0, 0, 2139, 2140, 5, 100, 0, 0, 2140, 2341, 5, 97, 0, 0, 2141, 2142, 5, 92, 0, 0, 2142, 2143, 5, 108, 0, 0, 2143, 2144, 5, 97, 0, 0, 2144, 2145, 5, 109, 0, 0, 2145, 2146, 5, 98, 0, 0, 2146, 2147, 5, 100, 0, 0, 2147, 2341, 5, 97, 0, 0, 2148, 2149, 5, 92, 0, 0, 2149, 2150, 5, 99, 0, 0, 2150, 2151, 5, 104, 0, 0, 2151, 2152, 5, 97, 0, 0, 2152, 2153, 5, 114, 0, 0, 2153, 2154, 5, 34, 0, 0, 2154, 2155, 5, 48, 0, 0, 2155, 2156, 5, 48, 0, 0, 2156, 2157, 5, 48, 0, 0, 2157, 2158, 5, 51, 0, 0, 2158, 2159, 5, 57, 0, 0, 2159, 2341, 5, 67, 0, 0, 2160, 2161, 5, 92, 0, 0, 2161, 2162, 5, 109, 0, 0, 2162, 2341, 5, 117, 0, 0, 2163, 2164, 5, 92, 0, 0, 2164, 2165, 5, 99, 0, 0, 2165, 2166, 5, 104, 0, 0, 2166, 2167, 5, 97, 0, 0, 2167, 2168, 5, 114, 0, 0, 2168, 2169, 5, 34, 0, 0, 2169, 2170, 5, 48, 0, 0, 2170, 2171, 5, 48, 0, 0, 2171, 2172, 5, 48, 0, 0, 2172, 2173, 5, 51, 0, 0, 2173, 2174, 5, 57, 0, 0, 2174, 2341, 5, 68, 0, 0, 2175, 2176, 5, 92, 0, 0, 2176, 2177, 5, 110, 0, 0, 2177, 2341, 5, 117, 0, 0, 2178, 2179, 5, 92, 0, 0, 2179, 2180, 5, 88, 0, 0, 2180, 2341, 5, 105, 0, 0, 2181, 2182, 5, 92, 0, 0, 2182, 2183, 5, 120, 0, 0, 2183, 2341, 5, 105, 0, 0, 2184, 2185, 5, 92, 0, 0, 2185, 2186, 5, 99, 0, 0, 2186, 2187, 5, 104, 0, 0, 2187, 2188, 5, 97, 0, 0, 2188, 2189, 5, 114, 0, 0, 2189, 2190, 5, 34, 0, 0, 2190, 2191, 5, 48, 0, 0, 2191, 2192, 5, 48, 0, 0, 2192, 2193, 5, 48, 0, 0, 2193, 2194, 5, 51, 0, 0, 2194, 2195, 5, 57, 0, 0, 2195, 2341, 5, 70, 0, 0, 2196, 2197, 5, 92, 0, 0, 2197, 2198, 5, 111, 0, 0, 2198, 2199, 5, 109, 0, 0, 2199, 2200, 5, 105, 0, 0, 2200, 2201, 5, 99, 0, 0, 2201, 2202, 5, 114, 0, 0, 2202, 2203, 5, 111, 0, 0, 2203, 2341, 5, 110, 0, 0, 2204, 2205, 5, 92, 0, 0, 2205, 2206, 5, 80, 0, 0, 2206, 2341, 5, 105, 0, 0, 2207, 2208, 5, 92, 0, 0, 2208, 2209, 5, 118, 0, 0, 2209, 2210, 5, 97, 0, 0, 2210, 2211, 5, 114, 0, 0, 2211, 2212, 5, 112, 0, 0, 2212, 2341, 5, 105, 0, 0, 2213, 2214, 5, 92, 0, 0, 2214, 2215, 5, 99, 0, 0, 2215, 2216, 5, 104, 0, 0, 2216, 2217, 5, 97, 0, 0, 2217, 2218, 5, 114, 0, 0, 2218, 2219, 5, 34, 0, 0, 2219, 2220, 5, 48, 0, 0, 2220, 2221, 5, 48, 0, 0, 2221, 2222, 5, 48, 0, 0, 2222, 2223, 5, 51, 0, 0, 2223, 2224, 5, 65, 0, 0, 2224, 2341, 5, 49, 0, 0, 2225, 2226, 5, 92, 0, 0, 2226, 2227, 5, 114, 0, 0, 2227, 2228, 5, 104, 0, 0, 2228, 2341, 5, 111, 0, 0, 2229, 2230, 5, 92, 0, 0, 2230, 2231, 5, 118, 0, 0, 2231, 2232, 5, 97, 0, 0, 2232, 2233, 5, 114, 0, 0, 2233, 2234, 5, 114, 0, 0, 2234, 2235, 5, 104, 0, 0, 2235, 2341, 5, 111, 0, 0, 2236, 2237, 5, 92, 0, 0, 2237, 2238, 5, 83, 0, 0, 2238, 2239, 5, 105, 0, 0, 2239, 2240, 5, 103, 0, 0, 2240, 2241, 5, 109, 0, 0, 2241, 2341, 5, 97, 0, 0, 2242, 2243, 5, 92, 0, 0, 2243, 2244, 5, 115, 0, 0, 2244, 2245, 5, 105, 0, 0, 2245, 2246, 5, 103, 0, 0, 2246, 2247, 5, 109, 0, 0, 2247, 2341, 5, 97, 0, 0, 2248, 2249, 5, 92, 0, 0, 2249, 2250, 5, 118, 0, 0, 2250, 2251, 5, 97, 0, 0, 2251, 2252, 5, 114, 0, 0, 2252, 2253, 5, 115, 0, 0, 2253, 2254, 5, 105, 0, 0, 2254, 2255, 5, 103, 0, 0, 2255, 2256, 5, 109, 0, 0, 2256, 2341, 5, 97, 0, 0, 2257, 2258, 5, 92, 0, 0, 2258, 2259, 5, 99, 0, 0, 2259, 2260, 5, 104, 0, 0, 2260, 2261, 5, 97, 0, 0, 2261, 2262, 5, 114, 0, 0, 2262, 2263, 5, 34, 0, 0, 2263, 2264, 5, 48, 0, 0, 2264, 2265, 5, 48, 0, 0, 2265, 2266, 5, 48, 0, 0, 2266, 2267, 5, 51, 0, 0, 2267, 2268, 5, 65, 0, 0, 2268, 2341, 5, 52, 0, 0, 2269, 2270, 5, 92, 0, 0, 2270, 2271, 5, 116, 0, 0, 2271, 2272, 5, 97, 0, 0, 2272, 2341, 5, 117, 0, 0, 2273, 2274, 5, 92, 0, 0, 2274, 2275, 5, 85, 0, 0, 2275, 2276, 5, 112, 0, 0, 2276, 2277, 5, 115, 0, 0, 2277, 2278, 5, 105, 0, 0, 2278, 2279, 5, 108, 0, 0, 2279, 2280, 5, 111, 0, 0, 2280, 2341, 5, 110, 0, 0, 2281, 2282, 5, 92, 0, 0, 2282, 2283, 5, 117, 0, 0, 2283, 2284, 5, 112, 0, 0, 2284, 2285, 5, 115, 0, 0, 2285, 2286, 5, 105, 0, 0, 2286, 2287, 5, 108, 0, 0, 2287, 2288, 5, 111, 0, 0, 2288, 2341, 5, 110, 0, 0, 2289, 2290, 5, 92, 0, 0, 2290, 2291, 5, 80, 0, 0, 2291, 2292, 5, 104, 0, 0, 2292, 2341, 5, 105, 0, 0, 2293, 2294, 5, 92, 0, 0, 2294, 2295, 5, 112, 0, 0, 2295, 2296, 5, 104, 0, 0, 2296, 2341, 5, 105, 0, 0, 2297, 2298, 5, 92, 0, 0, 2298, 2299, 5, 118, 0, 0, 2299, 2300, 5, 97, 0, 0, 2300, 2301, 5, 114, 0, 0, 2301, 2302, 5, 112, 0, 0, 2302, 2303, 5, 104, 0, 0, 2303, 2341, 5, 105, 0, 0, 2304, 2305, 5, 92, 0, 0, 2305, 2306, 5, 99, 0, 0, 2306, 2307, 5, 104, 0, 0, 2307, 2308, 5, 97, 0, 0, 2308, 2309, 5, 114, 0, 0, 2309, 2310, 5, 34, 0, 0, 2310, 2311, 5, 48, 0, 0, 2311, 2312, 5, 48, 0, 0, 2312, 2313, 5, 48, 0, 0, 2313, 2314, 5, 51, 0, 0, 2314, 2315, 5, 65, 0, 0, 2315, 2341, 5, 55, 0, 0, 2316, 2317, 5, 92, 0, 0, 2317, 2318, 5, 99, 0, 0, 2318, 2319, 5, 104, 0, 0, 2319, 2341, 5, 105, 0, 0, 2320, 2321, 5, 92, 0, 0, 2321, 2322, 5, 80, 0, 0, 2322, 2323, 5, 115, 0, 0, 2323, 2341, 5, 105, 0, 0, 2324, 2325, 5, 92, 0, 0, 2325, 2326, 5, 112, 0, 0, 2326, 2327, 5, 115, 0, 0, 2327, 2341, 5, 105, 0, 0, 2328, 2329, 5, 92, 0, 0, 2329, 2330, 5, 79, 0, 0, 2330, 2331, 5, 109, 0, 0, 2331, 2332, 5, 101, 0, 0, 2332, 2333, 5, 103, 0, 0, 2333, 2341, 5, 97, 0, 0, 2334, 2335, 5, 92, 0, 0, 2335, 2336, 5, 111, 0, 0, 2336, 2337, 5, 109, 0, 0, 2337, 2338, 5, 101, 0, 0, 2338, 2339, 5, 103, 0, 0, 2339, 2341, 5, 97, 0, 0, 2340, 1955, 1, 0, 0, 0, 2340, 1967, 1, 0, 0, 0, 2340, 1973, 1, 0, 0, 0, 2340, 1985, 1, 0, 0, 0, 2340, 1990, 1, 0, 0, 0, 2340, 1996, 1, 0, 0, 0, 2340, 2002, 1, 0, 0, 0, 2340, 2008, 1, 0, 0, 0, 2340, 2014, 1, 0, 0, 0, 2340, 2026, 1, 0, 0, 0, 2340, 2034, 1, 0, 0, 0, 2340, 2045, 1, 0, 0, 0, 2340, 2057, 1, 0, 0, 0, 2340, 2062, 1, 0, 0, 0, 2340, 2074, 1, 0, 0, 0, 2340, 2078, 1, 0, 0, 0, 2340, 2084, 1, 0, 0, 0, 2340, 2090, 1, 0, 0, 0, 2340, 2099, 1, 0, 0, 0, 2340, 2111, 1, 0, 0, 0, 2340, 2116, 1, 0, 0, 0, 2340, 2128, 1, 0, 0, 0, 2340, 2134, 1, 0, 0, 0, 2340, 2141, 1, 0, 0, 0, 2340, 2148, 1, 0, 0, 0, 2340, 2160, 1, 0, 0, 0, 2340, 2163, 1, 0, 0, 0, 2340, 2175, 1, 0, 0, 0, 2340, 2178, 1, 0, 0, 0, 2340, 2181, 1, 0, 0, 0, 2340, 2184, 1, 0, 0, 0, 2340, 2196, 1, 0, 0, 0, 2340, 2204, 1, 0, 0, 0, 2340, 2207, 1, 0, 0, 0, 2340, 2213, 1, 0, 0, 0, 2340, 2225, 1, 0, 0, 0, 2340, 2229, 1, 0, 0, 0, 2340, 2236, 1, 0, 0, 0, 2340, 2242, 1, 0, 0, 0, 2340, 2248, 1, 0, 0, 0, 2340, 2257, 1, 0, 0, 0, 2340, 2269, 1, 0, 0, 0, 2340, 2273, 1, 0, 0, 0, 2340, 2281, 1, 0, 0, 0, 2340, 2289, 1, 0, 0, 0, 2340, 2293, 1, 0, 0, 0, 2340, 2297, 1, 0, 0, 0, 2340, 2304, 1, 0, 0, 0, 2340, 2316, 1, 0, 0, 0, 2340, 2320, 1, 0, 0, 0, 2340, 2324, 1, 0, 0, 0, 2340, 2328, 1, 0, 0, 0, 2340, 2334, 1, 0, 0, 0, 2341, 390, 1, 0, 0, 0, 2342, 2344, 3, 389, 194, 0, 2343, 2345, 7, 4, 0, 0, 2344, 2343, 1, 0, 0, 0, 2344, 2345, 1, 0, 0, 0, 2345, 392, 1, 0, 0, 0, 2346, 2347, 5, 92, 0, 0, 2347, 2348, 5, 66, 0, 0, 2348, 2349, 5, 98, 0, 0, 2349, 2350, 5, 98, 0, 0, 2350, 2697, 5, 107, 0, 0, 2351, 2352, 5, 92, 0, 0, 2352, 2353, 5, 119, 0, 0, 2353, 2697, 5, 112, 0, 0, 2354, 2355, 5, 92, 0, 0, 2355, 2356, 5, 110, 0, 0, 2356, 2357, 5, 97, 0, 0, 2357, 2358, 5, 98, 0, 0, 2358, 2359, 5, 108, 0, 0, 2359, 2697, 5, 97, 0, 0, 2360, 2361, 5, 92, 0, 0, 2361, 2362, 5, 98, 0, 0, 2362, 2363, 5, 105, 0, 0, 2363, 2364, 5, 103, 0, 0, 2364, 2365, 5, 115, 0, 0, 2365, 2366, 5, 116, 0, 0, 2366, 2367, 5, 97, 0, 0, 2367, 2697, 5, 114, 0, 0, 2368, 2369, 5, 92, 0, 0, 2369, 2370, 5, 97, 0, 0, 2370, 2371, 5, 110, 0, 0, 2371, 2372, 5, 103, 0, 0, 2372, 2373, 5, 108, 0, 0, 2373, 2697, 5, 101, 0, 0, 2374, 2375, 5, 92, 0, 0, 2375, 2376, 5, 110, 0, 0, 2376, 2377, 5, 101, 0, 0, 2377, 2378, 5, 120, 0, 0, 2378, 2379, 5, 105, 0, 0, 2379, 2380, 5, 115, 0, 0, 2380, 2381, 5, 116, 0, 0, 2381, 2697, 5, 115, 0, 0, 2382, 2383, 5, 92, 0, 0, 2383, 2384, 5, 100, 0, 0, 2384, 2385, 5, 105, 0, 0, 2385, 2386, 5, 97, 0, 0, 2386, 2387, 5, 103, 0, 0, 2387, 2388, 5, 100, 0, 0, 2388, 2389, 5, 111, 0, 0, 2389, 2390, 5, 119, 0, 0, 2390, 2697, 5, 110, 0, 0, 2391, 2392, 5, 92, 0, 0, 2392, 2393, 5, 109, 0, 0, 2393, 2394, 5, 101, 0, 0, 2394, 2395, 5, 97, 0, 0, 2395, 2396, 5, 115, 0, 0, 2396, 2397, 5, 117, 0, 0, 2397, 2398, 5, 114, 0, 0, 2398, 2399, 5, 101, 0, 0, 2399, 2400, 5, 100, 0, 0, 2400, 2401, 5, 97, 0, 0, 2401, 2402, 5, 110, 0, 0, 2402, 2403, 5, 103, 0, 0, 2403, 2404, 5, 108, 0, 0, 2404, 2697, 5, 101, 0, 0, 2405, 2406, 5, 92, 0, 0, 2406, 2407, 5, 101, 0, 0, 2407, 2408, 5, 116, 0, 0, 2408, 2697, 5, 104, 0, 0, 2409, 2410, 5, 92, 0, 0, 2410, 2411, 5, 101, 0, 0, 2411, 2412, 5, 109, 0, 0, 2412, 2413, 5, 112, 0, 0, 2413, 2414, 5, 116, 0, 0, 2414, 2415, 5, 121, 0, 0, 2415, 2416, 5, 115, 0, 0, 2416, 2417, 5, 101, 0, 0, 2417, 2697, 5, 116, 0, 0, 2418, 2419, 5, 92, 0, 0, 2419, 2420, 5, 100, 0, 0, 2420, 2421, 5, 105, 0, 0, 2421, 2422, 5, 97, 0, 0, 2422, 2423, 5, 103, 0, 0, 2423, 2424, 5, 117, 0, 0, 2424, 2697, 5, 112, 0, 0, 2425, 2426, 5, 92, 0, 0, 2426, 2427, 5, 115, 0, 0, 2427, 2428, 5, 112, 0, 0, 2428, 2429, 5, 104, 0, 0, 2429, 2430, 5, 101, 0, 0, 2430, 2431, 5, 114, 0, 0, 2431, 2432, 5, 105, 0, 0, 2432, 2433, 5, 99, 0, 0, 2433, 2434, 5, 97, 0, 0, 2434, 2435, 5, 108, 0, 0, 2435, 2436, 5, 97, 0, 0, 2436, 2437, 5, 110, 0, 0, 2437, 2438, 5, 103, 0, 0, 2438, 2439, 5, 108, 0, 0, 2439, 2697, 5, 101, 0, 0, 2440, 2441, 5, 92, 0, 0, 2441, 2442, 5, 99, 0, 0, 2442, 2443, 5, 108, 0, 0, 2443, 2444, 5, 117, 0, 0, 2444, 2445, 5, 98, 0, 0, 2445, 2446, 5, 115, 0, 0, 2446, 2447, 5, 117, 0, 0, 2447, 2448, 5, 105, 0, 0, 2448, 2697, 5, 116, 0, 0, 2449, 2450, 5, 92, 0, 0, 2450, 2451, 5, 118, 0, 0, 2451, 2452, 5, 97, 0, 0, 2452, 2453, 5, 114, 0, 0, 2453, 2454, 5, 110, 0, 0, 2454, 2455, 5, 111, 0, 0, 2455, 2456, 5, 116, 0, 0, 2456, 2457, 5, 104, 0, 0, 2457, 2458, 5, 105, 0, 0, 2458, 2459, 5, 110, 0, 0, 2459, 2697, 5, 103, 0, 0, 2460, 2461, 5, 92, 0, 0, 2461, 2462, 5, 68, 0, 0, 2462, 2463, 5, 105, 0, 0, 2463, 2464, 5, 97, 0, 0, 2464, 2465, 5, 109, 0, 0, 2465, 2466, 5, 111, 0, 0, 2466, 2467, 5, 110, 0, 0, 2467, 2697, 5, 100, 0, 0, 2468, 2469, 5, 92, 0, 0, 2469, 2470, 5, 99, 0, 0, 2470, 2471, 5, 111, 0, 0, 2471, 2472, 5, 109, 0, 0, 2472, 2473, 5, 112, 0, 0, 2473, 2474, 5, 108, 0, 0, 2474, 2475, 5, 101, 0, 0, 2475, 2476, 5, 109, 0, 0, 2476, 2477, 5, 101, 0, 0, 2477, 2478, 5, 110, 0, 0, 2478, 2697, 5, 116, 0, 0, 2479, 2480, 5, 92, 0, 0, 2480, 2481, 5, 100, 0, 0, 2481, 2482, 5, 105, 0, 0, 2482, 2483, 5, 97, 0, 0, 2483, 2484, 5, 109, 0, 0, 2484, 2485, 5, 111, 0, 0, 2485, 2486, 5, 110, 0, 0, 2486, 2487, 5, 100, 0, 0, 2487, 2488, 5, 115, 0, 0, 2488, 2489, 5, 117, 0, 0, 2489, 2490, 5, 105, 0, 0, 2490, 2697, 5, 116, 0, 0, 2491, 2492, 5, 92, 0, 0, 2492, 2493, 5, 105, 0, 0, 2493, 2494, 5, 109, 0, 0, 2494, 2495, 5, 97, 0, 0, 2495, 2496, 5, 116, 0, 0, 2496, 2697, 5, 104, 0, 0, 2497, 2498, 5, 92, 0, 0, 2498, 2499, 5, 70, 0, 0, 2499, 2500, 5, 105, 0, 0, 2500, 2501, 5, 110, 0, 0, 2501, 2697, 5, 118, 0, 0, 2502, 2503, 5, 92, 0, 0, 2503, 2504, 5, 116, 0, 0, 2504, 2505, 5, 114, 0, 0, 2505, 2506, 5, 105, 0, 0, 2506, 2507, 5, 97, 0, 0, 2507, 2508, 5, 110, 0, 0, 2508, 2509, 5, 103, 0, 0, 2509, 2510, 5, 108, 0, 0, 2510, 2511, 5, 101, 0, 0, 2511, 2512, 5, 100, 0, 0, 2512, 2513, 5, 111, 0, 0, 2513, 2514, 5, 119, 0, 0, 2514, 2697, 5, 110, 0, 0, 2515, 2516, 5, 92, 0, 0, 2516, 2517, 5, 104, 0, 0, 2517, 2518, 5, 101, 0, 0, 2518, 2519, 5, 97, 0, 0, 2519, 2520, 5, 114, 0, 0, 2520, 2521, 5, 116, 0, 0, 2521, 2522, 5, 115, 0, 0, 2522, 2523, 5, 117, 0, 0, 2523, 2524, 5, 105, 0, 0, 2524, 2697, 5, 116, 0, 0, 2525, 2526, 5, 92, 0, 0, 2526, 2527, 5, 106, 0, 0, 2527, 2528, 5, 109, 0, 0, 2528, 2529, 5, 97, 0, 0, 2529, 2530, 5, 116, 0, 0, 2530, 2697, 5, 104, 0, 0, 2531, 2532, 5, 92, 0, 0, 2532, 2533, 5, 71, 0, 0, 2533, 2534, 5, 97, 0, 0, 2534, 2535, 5, 109, 0, 0, 2535, 2697, 5, 101, 0, 0, 2536, 2537, 5, 92, 0, 0, 2537, 2538, 5, 116, 0, 0, 2538, 2539, 5, 114, 0, 0, 2539, 2540, 5, 105, 0, 0, 2540, 2541, 5, 97, 0, 0, 2541, 2542, 5, 110, 0, 0, 2542, 2543, 5, 103, 0, 0, 2543, 2544, 5, 108, 0, 0, 2544, 2697, 5, 101, 0, 0, 2545, 2546, 5, 92, 0, 0, 2546, 2547, 5, 115, 0, 0, 2547, 2548, 5, 112, 0, 0, 2548, 2549, 5, 97, 0, 0, 2549, 2550, 5, 100, 0, 0, 2550, 2551, 5, 101, 0, 0, 2551, 2552, 5, 115, 0, 0, 2552, 2553, 5, 117, 0, 0, 2553, 2554, 5, 105, 0, 0, 2554, 2697, 5, 116, 0, 0, 2555, 2556, 5, 92, 0, 0, 2556, 2557, 5, 101, 0, 0, 2557, 2558, 5, 108, 0, 0, 2558, 2697, 5, 108, 0, 0, 2559, 2560, 5, 92, 0, 0, 2560, 2561, 5, 104, 0, 0, 2561, 2562, 5, 98, 0, 0, 2562, 2563, 5, 97, 0, 0, 2563, 2697, 5, 114, 0, 0, 2564, 2565, 5, 92, 0, 0, 2565, 2566, 5, 118, 0, 0, 2566, 2567, 5, 97, 0, 0, 2567, 2568, 5, 114, 0, 0, 2568, 2569, 5, 116, 0, 0, 2569, 2570, 5, 114, 0, 0, 2570, 2571, 5, 105, 0, 0, 2571, 2572, 5, 97, 0, 0, 2572, 2573, 5, 110, 0, 0, 2573, 2574, 5, 103, 0, 0, 2574, 2575, 5, 108, 0, 0, 2575, 2697, 5, 101, 0, 0, 2576, 2577, 5, 92, 0, 0, 2577, 2578, 5, 104, 0, 0, 2578, 2579, 5, 115, 0, 0, 2579, 2580, 5, 108, 0, 0, 2580, 2581, 5, 97, 0, 0, 2581, 2582, 5, 115, 0, 0, 2582, 2697, 5, 104, 0, 0, 2583, 2584, 5, 92, 0, 0, 2584, 2585, 5, 98, 0, 0, 2585, 2586, 5, 108, 0, 0, 2586, 2587, 5, 97, 0, 0, 2587, 2588, 5, 99, 0, 0, 2588, 2589, 5, 107, 0, 0, 2589, 2590, 5, 108, 0, 0, 2590, 2591, 5, 111, 0, 0, 2591, 2592, 5, 122, 0, 0, 2592, 2593, 5, 101, 0, 0, 2593, 2594, 5, 110, 0, 0, 2594, 2595, 5, 103, 0, 0, 2595, 2697, 5, 101, 0, 0, 2596, 2597, 5, 92, 0, 0, 2597, 2598, 5, 108, 0, 0, 2598, 2599, 5, 111, 0, 0, 2599, 2600, 5, 122, 0, 0, 2600, 2601, 5, 101, 0, 0, 2601, 2602, 5, 110, 0, 0, 2602, 2603, 5, 103, 0, 0, 2603, 2697, 5, 101, 0, 0, 2604, 2605, 5, 92, 0, 0, 2605, 2606, 5, 98, 0, 0, 2606, 2607, 5, 108, 0, 0, 2607, 2608, 5, 97, 0, 0, 2608, 2609, 5, 99, 0, 0, 2609, 2610, 5, 107, 0, 0, 2610, 2611, 5, 115, 0, 0, 2611, 2612, 5, 113, 0, 0, 2612, 2613, 5, 117, 0, 0, 2613, 2614, 5, 97, 0, 0, 2614, 2615, 5, 114, 0, 0, 2615, 2697, 5, 101, 0, 0, 2616, 2617, 5, 92, 0, 0, 2617, 2618, 5, 109, 0, 0, 2618, 2619, 5, 104, 0, 0, 2619, 2697, 5, 111, 0, 0, 2620, 2621, 5, 92, 0, 0, 2621, 2622, 5, 98, 0, 0, 2622, 2623, 5, 108, 0, 0, 2623, 2624, 5, 97, 0, 0, 2624, 2625, 5, 99, 0, 0, 2625, 2626, 5, 107, 0, 0, 2626, 2627, 5, 116, 0, 0, 2627, 2628, 5, 114, 0, 0, 2628, 2629, 5, 105, 0, 0, 2629, 2630, 5, 97, 0, 0, 2630, 2631, 5, 110, 0, 0, 2631, 2632, 5, 103, 0, 0, 2632, 2633, 5, 108, 0, 0, 2633, 2697, 5, 101, 0, 0, 2634, 2635, 5, 92, 0, 0, 2635, 2636, 5, 115, 0, 0, 2636, 2637, 5, 104, 0, 0, 2637, 2638, 5, 97, 0, 0, 2638, 2639, 5, 114, 0, 0, 2639, 2697, 5, 112, 0, 0, 2640, 2641, 5, 92, 0, 0, 2641, 2642, 5, 112, 0, 0, 2642, 2643, 5, 114, 0, 0, 2643, 2644, 5, 105, 0, 0, 2644, 2645, 5, 109, 0, 0, 2645, 2697, 5, 101, 0, 0, 2646, 2647, 5, 92, 0, 0, 2647, 2648, 5, 73, 0, 0, 2648, 2697, 5, 109, 0, 0, 2649, 2650, 5, 92, 0, 0, 2650, 2651, 5, 102, 0, 0, 2651, 2652, 5, 108, 0, 0, 2652, 2653, 5, 97, 0, 0, 2653, 2697, 5, 116, 0, 0, 2654, 2655, 5, 92, 0, 0, 2655, 2656, 5, 115, 0, 0, 2656, 2657, 5, 113, 0, 0, 2657, 2658, 5, 117, 0, 0, 2658, 2659, 5, 97, 0, 0, 2659, 2660, 5, 114, 0, 0, 2660, 2697, 5, 101, 0, 0, 2661, 2662, 5, 92, 0, 0, 2662, 2663, 5, 98, 0, 0, 2663, 2664, 5, 97, 0, 0, 2664, 2665, 5, 99, 0, 0, 2665, 2666, 5, 107, 0, 0, 2666, 2667, 5, 112, 0, 0, 2667, 2668, 5, 114, 0, 0, 2668, 2669, 5, 105, 0, 0, 2669, 2670, 5, 109, 0, 0, 2670, 2697, 5, 101, 0, 0, 2671, 2672, 5, 92, 0, 0, 2672, 2673, 5, 82, 0, 0, 2673, 2697, 5, 101, 0, 0, 2674, 2675, 5, 92, 0, 0, 2675, 2676, 5, 110, 0, 0, 2676, 2677, 5, 97, 0, 0, 2677, 2678, 5, 116, 0, 0, 2678, 2679, 5, 117, 0, 0, 2679, 2680, 5, 114, 0, 0, 2680, 2681, 5, 97, 0, 0, 2681, 2697, 5, 108, 0, 0, 2682, 2683, 5, 92, 0, 0, 2683, 2684, 5, 115, 0, 0, 2684, 2685, 5, 117, 0, 0, 2685, 2686, 5, 114, 0, 0, 2686, 2697, 5, 100, 0, 0, 2687, 2688, 5, 92, 0, 0, 2688, 2689, 5, 99, 0, 0, 2689, 2690, 5, 105, 0, 0, 2690, 2691, 5, 114, 0, 0, 2691, 2692, 5, 99, 0, 0, 2692, 2693, 5, 108, 0, 0, 2693, 2694, 5, 101, 0, 0, 2694, 2695, 5, 100, 0, 0, 2695, 2697, 5, 83, 0, 0, 2696, 2346, 1, 0, 0, 0, 2696, 2351, 1, 0, 0, 0, 2696, 2354, 1, 0, 0, 0, 2696, 2360, 1, 0, 0, 0, 2696, 2368, 1, 0, 0, 0, 2696, 2374, 1, 0, 0, 0, 2696, 2382, 1, 0, 0, 0, 2696, 2391, 1, 0, 0, 0, 2696, 2405, 1, 0, 0, 0, 2696, 2409, 1, 0, 0, 0, 2696, 2418, 1, 0, 0, 0, 2696, 2425, 1, 0, 0, 0, 2696, 2440, 1, 0, 0, 0, 2696, 2449, 1, 0, 0, 0, 2696, 2460, 1, 0, 0, 0, 2696, 2468, 1, 0, 0, 0, 2696, 2479, 1, 0, 0, 0, 2696, 2491, 1, 0, 0, 0, 2696, 2497, 1, 0, 0, 0, 2696, 2502, 1, 0, 0, 0, 2696, 2515, 1, 0, 0, 0, 2696, 2525, 1, 0, 0, 0, 2696, 2531, 1, 0, 0, 0, 2696, 2536, 1, 0, 0, 0, 2696, 2545, 1, 0, 0, 0, 2696, 2555, 1, 0, 0, 0, 2696, 2559, 1, 0, 0, 0, 2696, 2564, 1, 0, 0, 0, 2696, 2576, 1, 0, 0, 0, 2696, 2583, 1, 0, 0, 0, 2696, 2596, 1, 0, 0, 0, 2696, 2604, 1, 0, 0, 0, 2696, 2616, 1, 0, 0, 0, 2696, 2620, 1, 0, 0, 0, 2696, 2634, 1, 0, 0, 0, 2696, 2640, 1, 0, 0, 0, 2696, 2646, 1, 0, 0, 0, 2696, 2649, 1, 0, 0, 0, 2696, 2654, 1, 0, 0, 0, 2696, 2661, 1, 0, 0, 0, 2696, 2671, 1, 0, 0, 0, 2696, 2674, 1, 0, 0, 0, 2696, 2682, 1, 0, 0, 0, 2696, 2687, 1, 0, 0, 0, 2697, 394, 1, 0, 0, 0, 2698, 2700, 3, 393, 196, 0, 2699, 2701, 7, 4, 0, 0, 2700, 2699, 1, 0, 0, 0, 2700, 2701, 1, 0, 0, 0, 2701, 396, 1, 0, 0, 0, 2702, 2703, 5, 92, 0, 0, 2703, 2704, 5, 112, 0, 0, 2704, 2705, 5, 105, 0, 0, 2705, 398, 1, 0, 0, 0, 2706, 2707, 5, 92, 0, 0, 2707, 2708, 5, 105, 0, 0, 2708, 2709, 5, 110, 0, 0, 2709, 2710, 5, 102, 0, 0, 2710, 2711, 5, 116, 0, 0, 2711, 2712, 5, 121, 0, 0, 2712, 400, 1, 0, 0, 0, 2713, 2714, 5, 92, 0, 0, 2714, 2715, 5, 112, 0, 0, 2715, 2716, 5, 97, 0, 0, 2716, 2717, 5, 114, 0, 0, 2717, 2718, 5, 116, 0, 0, 2718, 2719, 5, 105, 0, 0, 2719, 2720, 5, 97, 0, 0, 2720, 2721, 5, 108, 0, 0, 2721, 402, 1, 0, 0, 0, 2722, 2730, 3, 399, 199, 0, 2723, 2724, 3, 91, 45, 0, 2724, 2725, 3, 399, 199, 0, 2725, 2730, 1, 0, 0, 0, 2726, 2727, 3, 399, 199, 0, 2727, 2728, 3, 385, 192, 0, 2728, 2730, 1, 0, 0, 0, 2729, 2722, 1, 0, 0, 0, 2729, 2723, 1, 0, 0, 0, 2729, 2726, 1, 0, 0, 0, 2730, 404, 1, 0, 0, 0, 2731, 2732, 5, 92, 0, 0, 2732, 2733, 5, 101, 0, 0, 2733, 2734, 5, 109, 0, 0, 2734, 2735, 5, 112, 0, 0, 2735, 2736, 5, 116, 0, 0, 2736, 2737, 5, 121, 0, 0, 2737, 2738, 5, 115, 0, 0, 2738, 2739, 5, 101, 0, 0, 2739, 2740, 5, 116, 0, 0, 2740, 406, 1, 0, 0, 0, 2741, 2746, 3, 397, 198, 0, 2742, 2746, 3, 401, 200, 0, 2743, 2746, 3, 403, 201, 0, 2744, 2746, 3, 405, 202, 0, 2745, 2741, 1, 0, 0, 0, 2745, 2742, 1, 0, 0, 0, 2745, 2743, 1, 0, 0, 0, 2745, 2744, 1, 0, 0, 0, 2746, 408, 1, 0, 0, 0, 2747, 2748, 5, 92, 0, 0, 2748, 2749, 5, 118, 0, 0, 2749, 2750, 5, 97, 0, 0, 2750, 2751, 5, 114, 0, 0, 2751, 2752, 5, 105, 0, 0, 2752, 2753, 5, 97, 0, 0, 2753, 2754, 5, 98, 0, 0, 2754, 2755, 5, 108, 0, 0, 2755, 2756, 5, 101, 0, 0, 2756, 410, 1, 0, 0, 0, 2757, 2762, 3, 391, 195, 0, 2758, 2762, 3, 395, 197, 0, 2759, 2762, 3, 355, 177, 0, 2760, 2762, 3, 357, 178, 0, 2761, 2757, 1, 0, 0, 0, 2761, 2758, 1, 0, 0, 0, 2761, 2759, 1, 0, 0, 0, 2761, 2760, 1, 0, 0, 0, 2762, 2763, 1, 0, 0, 0, 2763, 2761, 1, 0, 0, 0, 2763, 2764, 1, 0, 0, 0, 2764, 2786, 1, 0, 0, 0, 2765, 2784, 3, 333, 166, 0, 2766, 2772, 3, 109, 54, 0, 2767, 2773, 3, 391, 195, 0, 2768, 2773, 3, 395, 197, 0, 2769, 2773, 3, 355, 177, 0, 2770, 2773, 3, 357, 178, 0, 2771, 2773, 3, 341, 170, 0, 2772, 2767, 1, 0, 0, 0, 2772, 2768, 1, 0, 0, 0, 2772, 2769, 1, 0, 0, 0, 2772, 2770, 1, 0, 0, 0, 2772, 2771, 1, 0, 0, 0, 2773, 2774, 1, 0, 0, 0, 2774, 2772, 1, 0, 0, 0, 2774, 2775, 1, 0, 0, 0, 2775, 2776, 1, 0, 0, 0, 2776, 2777, 3, 111, 55, 0, 2777, 2785, 1, 0, 0, 0, 2778, 2783, 3, 391, 195, 0, 2779, 2783, 3, 395, 197, 0, 2780, 2783, 3, 355, 177, 0, 2781, 2783, 3, 357, 178, 0, 2782, 2778, 1, 0, 0, 0, 2782, 2779, 1, 0, 0, 0, 2782, 2780, 1, 0, 0, 0, 2782, 2781, 1, 0, 0, 0, 2783, 2785, 1, 0, 0, 0, 2784, 2766, 1, 0, 0, 0, 2784, 2782, 1, 0, 0, 0, 2785, 2787, 1, 0, 0, 0, 2786, 2765, 1, 0, 0, 0, 2786, 2787, 1, 0, 0, 0, 2787, 412, 1, 0, 0, 0, 2788, 2789, 3, 409, 204, 0, 2789, 2790, 3, 109, 54, 0, 2790, 2791, 3, 411, 205, 0, 2791, 2793, 3, 111, 55, 0, 2792, 2794, 3, 385, 192, 0, 2793, 2792, 1, 0, 0, 0, 2793, 2794, 1, 0, 0, 0, 2794, 414, 1, 0, 0, 0, 44, 0, 791, 812, 1063, 1397, 1450, 1481, 1503, 1527, 1535, 1581, 1652, 1717, 1725, 1727, 1743, 1777, 1815, 1820, 1829, 1835, 1845, 1852, 1854, 1860, 1865, 1881, 1901, 1921, 1945, 2340, 2344, 2696, 2700, 2729, 2745, 2761, 2763, 2772, 2774, 2782, 2784, 2786, 2793, 1, 6, 0, 0]
\ No newline at end of file diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.py b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.py new file mode 100755 index 0000000..a6f9882 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.py @@ -0,0 +1,1446 @@ +# Generated from PS.g4 by ANTLR 4.11.1 +# encoding: utf-8 +from __future__ import print_function +from antlr4 import * +from io import StringIO +import sys + + +def serializedATN(): + return [ + 4, 0, 194, 2795, 6, -1, 2, 0, 7, 0, 2, 1, 7, 1, 2, 2, 7, 2, 2, 3, 7, 3, 2, 4, 7, 4, 2, 5, 7, + 5, 2, 6, 7, 6, 2, 7, 7, 7, 2, 8, 7, 8, 2, 9, 7, 9, 2, 10, 7, 10, 2, 11, 7, 11, 2, 12, 7, 12, + 2, 13, 7, 13, 2, 14, 7, 14, 2, 15, 7, 15, 2, 16, 7, 16, 2, 17, 7, 17, 2, 18, 7, 18, 2, 19, + 7, 19, 2, 20, 7, 20, 2, 21, 7, 21, 2, 22, 7, 22, 2, 23, 7, 23, 2, 24, 7, 24, 2, 25, 7, 25, + 2, 26, 7, 26, 2, 27, 7, 27, 2, 28, 7, 28, 2, 29, 7, 29, 2, 30, 7, 30, 2, 31, 7, 31, 2, 32, + 7, 32, 2, 33, 7, 33, 2, 34, 7, 34, 2, 35, 7, 35, 2, 36, 7, 36, 2, 37, 7, 37, 2, 38, 7, 38, + 2, 39, 7, 39, 2, 40, 7, 40, 2, 41, 7, 41, 2, 42, 7, 42, 2, 43, 7, 43, 2, 44, 7, 44, 2, 45, + 7, 45, 2, 46, 7, 46, 2, 47, 7, 47, 2, 48, 7, 48, 2, 49, 7, 49, 2, 50, 7, 50, 2, 51, 7, 51, + 2, 52, 7, 52, 2, 53, 7, 53, 2, 54, 7, 54, 2, 55, 7, 55, 2, 56, 7, 56, 2, 57, 7, 57, 2, 58, + 7, 58, 2, 59, 7, 59, 2, 60, 7, 60, 2, 61, 7, 61, 2, 62, 7, 62, 2, 63, 7, 63, 2, 64, 7, 64, + 2, 65, 7, 65, 2, 66, 7, 66, 2, 67, 7, 67, 2, 68, 7, 68, 2, 69, 7, 69, 2, 70, 7, 70, 2, 71, + 7, 71, 2, 72, 7, 72, 2, 73, 7, 73, 2, 74, 7, 74, 2, 75, 7, 75, 2, 76, 7, 76, 2, 77, 7, 77, + 2, 78, 7, 78, 2, 79, 7, 79, 2, 80, 7, 80, 2, 81, 7, 81, 2, 82, 7, 82, 2, 83, 7, 83, 2, 84, + 7, 84, 2, 85, 7, 85, 2, 86, 7, 86, 2, 87, 7, 87, 2, 88, 7, 88, 2, 89, 7, 89, 2, 90, 7, 90, + 2, 91, 7, 91, 2, 92, 7, 92, 2, 93, 7, 93, 2, 94, 7, 94, 2, 95, 7, 95, 2, 96, 7, 96, 2, 97, + 7, 97, 2, 98, 7, 98, 2, 99, 7, 99, 2, 100, 7, 100, 2, 101, 7, 101, 2, 102, 7, 102, 2, 103, + 7, 103, 2, 104, 7, 104, 2, 105, 7, 105, 2, 106, 7, 106, 2, 107, 7, 107, 2, 108, 7, 108, + 2, 109, 7, 109, 2, 110, 7, 110, 2, 111, 7, 111, 2, 112, 7, 112, 2, 113, 7, 113, 2, 114, + 7, 114, 2, 115, 7, 115, 2, 116, 7, 116, 2, 117, 7, 117, 2, 118, 7, 118, 2, 119, 7, 119, + 2, 120, 7, 120, 2, 121, 7, 121, 2, 122, 7, 122, 2, 123, 7, 123, 2, 124, 7, 124, 2, 125, + 7, 125, 2, 126, 7, 126, 2, 127, 7, 127, 2, 128, 7, 128, 2, 129, 7, 129, 2, 130, 7, 130, + 2, 131, 7, 131, 2, 132, 7, 132, 2, 133, 7, 133, 2, 134, 7, 134, 2, 135, 7, 135, 2, 136, + 7, 136, 2, 137, 7, 137, 2, 138, 7, 138, 2, 139, 7, 139, 2, 140, 7, 140, 2, 141, 7, 141, + 2, 142, 7, 142, 2, 143, 7, 143, 2, 144, 7, 144, 2, 145, 7, 145, 2, 146, 7, 146, 2, 147, + 7, 147, 2, 148, 7, 148, 2, 149, 7, 149, 2, 150, 7, 150, 2, 151, 7, 151, 2, 152, 7, 152, + 2, 153, 7, 153, 2, 154, 7, 154, 2, 155, 7, 155, 2, 156, 7, 156, 2, 157, 7, 157, 2, 158, + 7, 158, 2, 159, 7, 159, 2, 160, 7, 160, 2, 161, 7, 161, 2, 162, 7, 162, 2, 163, 7, 163, + 2, 164, 7, 164, 2, 165, 7, 165, 2, 166, 7, 166, 2, 167, 7, 167, 2, 168, 7, 168, 2, 169, + 7, 169, 2, 170, 7, 170, 2, 171, 7, 171, 2, 172, 7, 172, 2, 173, 7, 173, 2, 174, 7, 174, + 2, 175, 7, 175, 2, 176, 7, 176, 2, 177, 7, 177, 2, 178, 7, 178, 2, 179, 7, 179, 2, 180, + 7, 180, 2, 181, 7, 181, 2, 182, 7, 182, 2, 183, 7, 183, 2, 184, 7, 184, 2, 185, 7, 185, + 2, 186, 7, 186, 2, 187, 7, 187, 2, 188, 7, 188, 2, 189, 7, 189, 2, 190, 7, 190, 2, 191, + 7, 191, 2, 192, 7, 192, 2, 193, 7, 193, 2, 194, 7, 194, 2, 195, 7, 195, 2, 196, 7, 196, + 2, 197, 7, 197, 2, 198, 7, 198, 2, 199, 7, 199, 2, 200, 7, 200, 2, 201, 7, 201, 2, 202, + 7, 202, 2, 203, 7, 203, 2, 204, 7, 204, 2, 205, 7, 205, 2, 206, 7, 206, 1, 0, 1, 0, 1, + 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, + 2, 1, 2, 1, 2, 1, 2, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 4, 1, 4, 1, 4, 1, 4, 1, 4, 1, + 4, 1, 4, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 5, 1, 6, 1, 6, 1, 6, 1, + 6, 1, 6, 1, 7, 1, 7, 1, 7, 1, 7, 1, 7, 1, 7, 1, 8, 1, 8, 1, 8, 1, 8, 1, 8, 1, 8, 1, 8, 1, 9, 1, + 9, 1, 9, 1, 9, 1, 9, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 11, 1, 11, 1, 11, + 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 11, 1, 12, 1, 12, 1, 12, 1, 12, 1, 12, + 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, + 1, 13, 1, 13, 1, 13, 1, 14, 1, 14, 1, 14, 1, 14, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, + 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 15, 1, 16, 1, 16, 1, 16, 1, 16, 1, 16, 1, 16, 1, 17, + 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, + 1, 18, 1, 18, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 20, 1, 20, + 1, 20, 1, 20, 1, 20, 1, 20, 1, 20, 1, 20, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, 1, 21, + 1, 21, 1, 21, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 22, 1, 23, + 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 23, 1, 24, 1, 24, 1, 24, + 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 24, 1, 25, 1, 25, + 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, + 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 26, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, + 1, 27, 1, 27, 1, 27, 1, 27, 1, 27, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, + 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 30, 1, 30, 1, 30, + 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, + 1, 31, 1, 31, 1, 31, 1, 31, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, + 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 34, 1, 34, 1, 34, + 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, + 1, 35, 1, 35, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 37, 1, 37, + 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, + 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 38, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, + 1, 39, 1, 39, 1, 40, 1, 40, 1, 40, 1, 41, 1, 41, 1, 41, 1, 41, 1, 41, 1, 42, 1, 42, 1, 42, + 1, 42, 1, 42, 1, 42, 1, 42, 1, 42, 1, 43, 1, 43, 1, 44, 4, 44, 790, 8, 44, 11, 44, 12, 44, + 791, 1, 44, 1, 44, 1, 45, 1, 45, 1, 45, 1, 45, 1, 45, 1, 46, 1, 46, 1, 47, 1, 47, 1, 48, + 1, 48, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 3, 49, 813, 8, 49, 1, 50, 1, 50, 1, 51, + 1, 51, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 52, 1, 53, 1, 53, 1, 53, 1, 53, + 1, 53, 1, 53, 1, 53, 1, 53, 1, 54, 1, 54, 1, 55, 1, 55, 1, 56, 1, 56, 1, 56, 1, 57, 1, 57, + 1, 57, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 58, 1, 59, 1, 59, 1, 59, 1, 59, + 1, 59, 1, 59, 1, 59, 1, 59, 1, 60, 1, 60, 1, 61, 1, 61, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, + 1, 62, 1, 62, 1, 62, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 63, 1, 64, 1, 64, + 1, 65, 1, 65, 1, 65, 1, 65, 1, 65, 1, 65, 1, 65, 1, 66, 1, 66, 1, 66, 1, 66, 1, 66, 1, 66, + 1, 66, 1, 67, 1, 67, 1, 67, 1, 67, 1, 67, 1, 67, 1, 68, 1, 68, 1, 68, 1, 69, 1, 69, 1, 69, + 1, 69, 1, 69, 1, 69, 1, 69, 1, 69, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, 1, 70, + 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 71, 1, 72, 1, 72, 1, 72, + 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 72, 1, 73, 1, 73, 1, 73, 1, 73, 1, 73, 1, 73, + 1, 73, 1, 74, 1, 74, 1, 74, 1, 74, 1, 74, 1, 74, 1, 74, 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, + 1, 75, 1, 75, 1, 75, 1, 75, 1, 75, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, 1, 76, + 1, 76, 1, 76, 1, 77, 1, 77, 1, 77, 1, 77, 1, 77, 1, 77, 1, 78, 1, 78, 1, 78, 1, 78, 1, 78, + 1, 78, 1, 78, 1, 79, 1, 79, 1, 79, 1, 79, 1, 79, 1, 79, 1, 79, 1, 80, 1, 80, 1, 80, 1, 80, + 1, 80, 1, 80, 1, 80, 1, 80, 1, 81, 1, 81, 1, 81, 1, 81, 1, 81, 1, 82, 1, 82, 1, 82, 1, 82, + 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, + 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, + 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, + 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 1, 82, 3, 82, + 1064, 8, 82, 1, 83, 1, 83, 1, 83, 1, 83, 1, 83, 1, 84, 1, 84, 1, 84, 1, 84, 1, 84, 1, 85, + 1, 85, 1, 85, 1, 85, 1, 85, 1, 85, 1, 86, 1, 86, 1, 86, 1, 86, 1, 86, 1, 87, 1, 87, 1, 87, + 1, 87, 1, 88, 1, 88, 1, 88, 1, 88, 1, 88, 1, 89, 1, 89, 1, 89, 1, 89, 1, 89, 1, 90, 1, 90, + 1, 90, 1, 90, 1, 90, 1, 91, 1, 91, 1, 91, 1, 91, 1, 91, 1, 92, 1, 92, 1, 92, 1, 92, 1, 92, + 1, 93, 1, 93, 1, 93, 1, 93, 1, 93, 1, 94, 1, 94, 1, 94, 1, 94, 1, 94, 1, 95, 1, 95, 1, 95, + 1, 95, 1, 95, 1, 95, 1, 95, 1, 95, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, 1, 96, + 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 97, 1, 98, 1, 98, 1, 98, 1, 98, 1, 98, + 1, 98, 1, 98, 1, 98, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 99, 1, 100, 1, 100, + 1, 100, 1, 100, 1, 100, 1, 100, 1, 100, 1, 100, 1, 101, 1, 101, 1, 101, 1, 101, 1, 101, + 1, 101, 1, 102, 1, 102, 1, 102, 1, 102, 1, 102, 1, 102, 1, 103, 1, 103, 1, 103, 1, 103, + 1, 103, 1, 103, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 104, 1, 105, + 1, 105, 1, 105, 1, 105, 1, 105, 1, 105, 1, 105, 1, 105, 1, 106, 1, 106, 1, 106, 1, 106, + 1, 106, 1, 106, 1, 106, 1, 106, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, 1, 107, + 1, 107, 1, 107, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, 1, 108, + 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 109, 1, 110, 1, 110, + 1, 110, 1, 110, 1, 110, 1, 110, 1, 110, 1, 111, 1, 111, 1, 111, 1, 111, 1, 111, 1, 111, + 1, 111, 1, 111, 1, 112, 1, 112, 1, 112, 1, 112, 1, 112, 1, 112, 1, 112, 1, 113, 1, 113, + 1, 113, 1, 113, 1, 113, 1, 113, 1, 113, 1, 113, 1, 114, 1, 114, 1, 114, 1, 114, 1, 114, + 1, 114, 1, 114, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 115, 1, 116, + 1, 116, 1, 116, 1, 116, 1, 117, 1, 117, 1, 117, 1, 117, 1, 118, 1, 118, 1, 118, 1, 118, + 1, 118, 1, 118, 1, 119, 1, 119, 1, 119, 1, 119, 1, 119, 1, 120, 1, 120, 1, 120, 1, 120, + 1, 120, 1, 120, 1, 121, 1, 121, 1, 121, 1, 121, 1, 121, 1, 122, 1, 122, 1, 122, 1, 122, + 1, 122, 1, 123, 1, 123, 1, 123, 1, 123, 1, 123, 1, 123, 1, 123, 1, 124, 1, 124, 1, 124, + 1, 124, 1, 124, 1, 124, 1, 125, 1, 125, 1, 125, 1, 125, 1, 125, 1, 126, 1, 126, 1, 126, + 1, 126, 1, 126, 1, 127, 1, 127, 1, 127, 1, 127, 1, 127, 1, 128, 1, 128, 1, 128, 1, 128, + 1, 129, 1, 129, 1, 129, 1, 129, 1, 129, 1, 129, 1, 130, 1, 130, 1, 130, 1, 130, 1, 130, + 1, 131, 1, 131, 1, 131, 1, 131, 1, 131, 1, 132, 1, 132, 1, 132, 1, 132, 1, 132, 1, 133, + 1, 133, 1, 133, 1, 133, 1, 133, 1, 134, 1, 134, 1, 134, 1, 134, 1, 134, 1, 135, 1, 135, + 1, 135, 1, 135, 1, 135, 1, 136, 1, 136, 1, 136, 1, 136, 1, 136, 1, 136, 1, 136, 3, 136, + 1398, 8, 136, 1, 137, 1, 137, 1, 137, 1, 137, 1, 137, 1, 138, 1, 138, 1, 138, 1, 138, + 1, 138, 1, 138, 1, 138, 1, 139, 1, 139, 1, 139, 1, 139, 1, 139, 1, 139, 1, 139, 1, 140, + 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, + 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, + 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 1, 140, 3, 140, 1451, + 8, 140, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, 1, 141, + 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, + 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 1, 142, 3, 142, 1482, 8, 142, + 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, + 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 1, 143, 3, 143, 1504, + 8, 143, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, + 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, 1, 144, + 1, 144, 3, 144, 1528, 8, 144, 1, 145, 1, 145, 1, 145, 1, 145, 1, 145, 1, 145, 3, 145, + 1536, 8, 145, 1, 146, 1, 146, 1, 146, 1, 146, 1, 146, 1, 146, 1, 146, 1, 147, 1, 147, + 1, 147, 1, 147, 1, 147, 1, 147, 1, 148, 1, 148, 1, 148, 1, 148, 1, 148, 1, 149, 1, 149, + 1, 149, 1, 149, 1, 149, 1, 149, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, + 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, 1, 150, + 1, 150, 1, 150, 3, 150, 1582, 8, 150, 1, 151, 1, 151, 1, 151, 1, 151, 1, 151, 1, 151, + 1, 151, 1, 151, 1, 152, 1, 152, 1, 152, 1, 152, 1, 152, 1, 153, 1, 153, 1, 153, 1, 153, + 1, 153, 1, 153, 1, 153, 1, 153, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, + 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 154, 1, 155, 1, 155, 1, 155, 1, 155, + 1, 155, 1, 155, 1, 155, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, 1, 156, + 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 157, 1, 158, 1, 158, 1, 158, + 1, 158, 1, 158, 1, 158, 1, 158, 1, 158, 1, 159, 1, 159, 1, 159, 3, 159, 1653, 8, 159, + 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, 1, 160, + 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 161, 1, 162, 1, 162, + 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 162, 1, 163, 1, 163, + 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 163, 1, 164, 1, 164, 1, 165, 1, 165, + 1, 165, 1, 166, 1, 166, 1, 167, 1, 167, 1, 168, 1, 168, 1, 169, 1, 169, 1, 170, 1, 170, + 1, 171, 1, 171, 1, 172, 1, 172, 1, 173, 1, 173, 5, 173, 1716, 8, 173, 10, 173, 12, 173, + 1719, 9, 173, 1, 173, 1, 173, 1, 173, 4, 173, 1724, 8, 173, 11, 173, 12, 173, 1725, + 3, 173, 1728, 8, 173, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, + 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 1, 174, 3, 174, 1744, 8, 174, 1, 175, 1, 175, + 1, 176, 1, 176, 1, 177, 1, 177, 1, 178, 1, 178, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, + 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, + 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 1, 179, 3, 179, 1778, 8, 179, + 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, + 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, + 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, 1, 180, + 1, 180, 1, 180, 1, 180, 3, 180, 1816, 8, 180, 1, 181, 4, 181, 1819, 8, 181, 11, 181, + 12, 181, 1820, 1, 181, 1, 181, 1, 181, 1, 181, 1, 181, 5, 181, 1828, 8, 181, 10, 181, + 12, 181, 1831, 9, 181, 1, 181, 5, 181, 1834, 8, 181, 10, 181, 12, 181, 1837, 9, 181, + 1, 181, 1, 181, 1, 181, 1, 181, 1, 181, 5, 181, 1844, 8, 181, 10, 181, 12, 181, 1847, + 9, 181, 1, 181, 1, 181, 4, 181, 1851, 8, 181, 11, 181, 12, 181, 1852, 3, 181, 1855, + 8, 181, 1, 182, 1, 182, 1, 182, 1, 182, 3, 182, 1861, 8, 182, 1, 182, 4, 182, 1864, + 8, 182, 11, 182, 12, 182, 1865, 1, 183, 1, 183, 1, 183, 1, 183, 1, 184, 1, 184, 1, 185, + 1, 185, 1, 185, 1, 185, 1, 185, 1, 185, 1, 185, 1, 185, 3, 185, 1882, 8, 185, 1, 186, + 1, 186, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, + 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 1, 187, 3, 187, 1902, 8, 187, 1, 188, 1, 188, + 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, + 1, 189, 1, 189, 1, 189, 1, 189, 1, 189, 3, 189, 1922, 8, 189, 1, 190, 1, 190, 1, 190, + 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, + 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 1, 190, 3, 190, 1946, 8, 190, + 1, 191, 1, 191, 1, 192, 1, 192, 1, 192, 1, 193, 1, 193, 1, 193, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, + 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 1, 194, 3, 194, 2341, 8, 194, + 1, 195, 1, 195, 3, 195, 2345, 8, 195, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, 1, 196, + 1, 196, 1, 196, 1, 196, 3, 196, 2697, 8, 196, 1, 197, 1, 197, 3, 197, 2701, 8, 197, + 1, 198, 1, 198, 1, 198, 1, 198, 1, 199, 1, 199, 1, 199, 1, 199, 1, 199, 1, 199, 1, 199, + 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 200, 1, 201, 1, 201, + 1, 201, 1, 201, 1, 201, 1, 201, 1, 201, 3, 201, 2730, 8, 201, 1, 202, 1, 202, 1, 202, + 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 202, 1, 203, 1, 203, 1, 203, 1, 203, + 3, 203, 2746, 8, 203, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, 1, 204, + 1, 204, 1, 204, 1, 205, 1, 205, 1, 205, 1, 205, 4, 205, 2762, 8, 205, 11, 205, 12, 205, + 2763, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 4, 205, 2773, 8, 205, + 11, 205, 12, 205, 2774, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 1, 205, 3, 205, 2783, + 8, 205, 3, 205, 2785, 8, 205, 3, 205, 2787, 8, 205, 1, 206, 1, 206, 1, 206, 1, 206, + 1, 206, 3, 206, 2794, 8, 206, 1, 1717, 0, 207, 1, 1, 3, 2, 5, 3, 7, 4, 9, 5, 11, 6, 13, + 7, 15, 8, 17, 9, 19, 10, 21, 11, 23, 12, 25, 13, 27, 14, 29, 15, 31, 16, 33, 17, 35, 18, + 37, 19, 39, 20, 41, 21, 43, 22, 45, 23, 47, 24, 49, 25, 51, 26, 53, 27, 55, 28, 57, 29, + 59, 30, 61, 31, 63, 32, 65, 33, 67, 34, 69, 35, 71, 36, 73, 37, 75, 38, 77, 39, 79, 40, + 81, 41, 83, 42, 85, 43, 87, 44, 89, 45, 91, 46, 93, 47, 95, 48, 97, 49, 99, 50, 101, + 51, 103, 52, 105, 53, 107, 54, 109, 55, 111, 56, 113, 57, 115, 58, 117, 59, 119, 60, + 121, 61, 123, 62, 125, 63, 127, 64, 129, 65, 131, 66, 133, 67, 135, 68, 137, 69, 139, + 70, 141, 71, 143, 72, 145, 73, 147, 74, 149, 75, 151, 76, 153, 77, 155, 78, 157, 79, + 159, 80, 161, 81, 163, 82, 165, 83, 167, 84, 169, 85, 171, 86, 173, 87, 175, 88, 177, + 89, 179, 90, 181, 91, 183, 92, 185, 93, 187, 94, 189, 95, 191, 96, 193, 97, 195, 98, + 197, 99, 199, 100, 201, 101, 203, 102, 205, 103, 207, 104, 209, 105, 211, 106, 213, + 107, 215, 108, 217, 109, 219, 110, 221, 111, 223, 112, 225, 113, 227, 114, 229, + 115, 231, 116, 233, 117, 235, 118, 237, 119, 239, 120, 241, 121, 243, 122, 245, + 123, 247, 124, 249, 125, 251, 126, 253, 127, 255, 128, 257, 129, 259, 130, 261, + 131, 263, 132, 265, 133, 267, 134, 269, 135, 271, 136, 273, 137, 275, 138, 277, + 139, 279, 140, 281, 141, 283, 142, 285, 143, 287, 144, 289, 145, 291, 146, 293, + 147, 295, 148, 297, 149, 299, 150, 301, 151, 303, 152, 305, 153, 307, 154, 309, + 155, 311, 156, 313, 157, 315, 158, 317, 159, 319, 160, 321, 161, 323, 162, 325, + 163, 327, 164, 329, 165, 331, 166, 333, 167, 335, 168, 337, 169, 339, 170, 341, + 171, 343, 172, 345, 0, 347, 173, 349, 174, 351, 175, 353, 176, 355, 0, 357, 0, 359, + 177, 361, 178, 363, 179, 365, 180, 367, 181, 369, 182, 371, 183, 373, 184, 375, + 185, 377, 186, 379, 187, 381, 188, 383, 189, 385, 0, 387, 190, 389, 0, 391, 191, + 393, 0, 395, 192, 397, 0, 399, 0, 401, 0, 403, 0, 405, 0, 407, 193, 409, 0, 411, 0, + 413, 194, 1, 0, 5, 3, 0, 9, 10, 13, 13, 32, 32, 2, 0, 65, 90, 97, 122, 4, 0, 65, 68, 70, + 90, 97, 100, 102, 122, 1, 0, 48, 57, 1, 0, 32, 32, 2943, 0, 1, 1, 0, 0, 0, 0, 3, 1, 0, 0, + 0, 0, 5, 1, 0, 0, 0, 0, 7, 1, 0, 0, 0, 0, 9, 1, 0, 0, 0, 0, 11, 1, 0, 0, 0, 0, 13, 1, 0, 0, 0, + 0, 15, 1, 0, 0, 0, 0, 17, 1, 0, 0, 0, 0, 19, 1, 0, 0, 0, 0, 21, 1, 0, 0, 0, 0, 23, 1, 0, 0, 0, + 0, 25, 1, 0, 0, 0, 0, 27, 1, 0, 0, 0, 0, 29, 1, 0, 0, 0, 0, 31, 1, 0, 0, 0, 0, 33, 1, 0, 0, 0, + 0, 35, 1, 0, 0, 0, 0, 37, 1, 0, 0, 0, 0, 39, 1, 0, 0, 0, 0, 41, 1, 0, 0, 0, 0, 43, 1, 0, 0, 0, + 0, 45, 1, 0, 0, 0, 0, 47, 1, 0, 0, 0, 0, 49, 1, 0, 0, 0, 0, 51, 1, 0, 0, 0, 0, 53, 1, 0, 0, 0, + 0, 55, 1, 0, 0, 0, 0, 57, 1, 0, 0, 0, 0, 59, 1, 0, 0, 0, 0, 61, 1, 0, 0, 0, 0, 63, 1, 0, 0, 0, + 0, 65, 1, 0, 0, 0, 0, 67, 1, 0, 0, 0, 0, 69, 1, 0, 0, 0, 0, 71, 1, 0, 0, 0, 0, 73, 1, 0, 0, 0, + 0, 75, 1, 0, 0, 0, 0, 77, 1, 0, 0, 0, 0, 79, 1, 0, 0, 0, 0, 81, 1, 0, 0, 0, 0, 83, 1, 0, 0, 0, + 0, 85, 1, 0, 0, 0, 0, 87, 1, 0, 0, 0, 0, 89, 1, 0, 0, 0, 0, 91, 1, 0, 0, 0, 0, 93, 1, 0, 0, 0, + 0, 95, 1, 0, 0, 0, 0, 97, 1, 0, 0, 0, 0, 99, 1, 0, 0, 0, 0, 101, 1, 0, 0, 0, 0, 103, 1, 0, 0, + 0, 0, 105, 1, 0, 0, 0, 0, 107, 1, 0, 0, 0, 0, 109, 1, 0, 0, 0, 0, 111, 1, 0, 0, 0, 0, 113, + 1, 0, 0, 0, 0, 115, 1, 0, 0, 0, 0, 117, 1, 0, 0, 0, 0, 119, 1, 0, 0, 0, 0, 121, 1, 0, 0, 0, + 0, 123, 1, 0, 0, 0, 0, 125, 1, 0, 0, 0, 0, 127, 1, 0, 0, 0, 0, 129, 1, 0, 0, 0, 0, 131, 1, + 0, 0, 0, 0, 133, 1, 0, 0, 0, 0, 135, 1, 0, 0, 0, 0, 137, 1, 0, 0, 0, 0, 139, 1, 0, 0, 0, 0, + 141, 1, 0, 0, 0, 0, 143, 1, 0, 0, 0, 0, 145, 1, 0, 0, 0, 0, 147, 1, 0, 0, 0, 0, 149, 1, 0, + 0, 0, 0, 151, 1, 0, 0, 0, 0, 153, 1, 0, 0, 0, 0, 155, 1, 0, 0, 0, 0, 157, 1, 0, 0, 0, 0, 159, + 1, 0, 0, 0, 0, 161, 1, 0, 0, 0, 0, 163, 1, 0, 0, 0, 0, 165, 1, 0, 0, 0, 0, 167, 1, 0, 0, 0, + 0, 169, 1, 0, 0, 0, 0, 171, 1, 0, 0, 0, 0, 173, 1, 0, 0, 0, 0, 175, 1, 0, 0, 0, 0, 177, 1, + 0, 0, 0, 0, 179, 1, 0, 0, 0, 0, 181, 1, 0, 0, 0, 0, 183, 1, 0, 0, 0, 0, 185, 1, 0, 0, 0, 0, + 187, 1, 0, 0, 0, 0, 189, 1, 0, 0, 0, 0, 191, 1, 0, 0, 0, 0, 193, 1, 0, 0, 0, 0, 195, 1, 0, + 0, 0, 0, 197, 1, 0, 0, 0, 0, 199, 1, 0, 0, 0, 0, 201, 1, 0, 0, 0, 0, 203, 1, 0, 0, 0, 0, 205, + 1, 0, 0, 0, 0, 207, 1, 0, 0, 0, 0, 209, 1, 0, 0, 0, 0, 211, 1, 0, 0, 0, 0, 213, 1, 0, 0, 0, + 0, 215, 1, 0, 0, 0, 0, 217, 1, 0, 0, 0, 0, 219, 1, 0, 0, 0, 0, 221, 1, 0, 0, 0, 0, 223, 1, + 0, 0, 0, 0, 225, 1, 0, 0, 0, 0, 227, 1, 0, 0, 0, 0, 229, 1, 0, 0, 0, 0, 231, 1, 0, 0, 0, 0, + 233, 1, 0, 0, 0, 0, 235, 1, 0, 0, 0, 0, 237, 1, 0, 0, 0, 0, 239, 1, 0, 0, 0, 0, 241, 1, 0, + 0, 0, 0, 243, 1, 0, 0, 0, 0, 245, 1, 0, 0, 0, 0, 247, 1, 0, 0, 0, 0, 249, 1, 0, 0, 0, 0, 251, + 1, 0, 0, 0, 0, 253, 1, 0, 0, 0, 0, 255, 1, 0, 0, 0, 0, 257, 1, 0, 0, 0, 0, 259, 1, 0, 0, 0, + 0, 261, 1, 0, 0, 0, 0, 263, 1, 0, 0, 0, 0, 265, 1, 0, 0, 0, 0, 267, 1, 0, 0, 0, 0, 269, 1, + 0, 0, 0, 0, 271, 1, 0, 0, 0, 0, 273, 1, 0, 0, 0, 0, 275, 1, 0, 0, 0, 0, 277, 1, 0, 0, 0, 0, + 279, 1, 0, 0, 0, 0, 281, 1, 0, 0, 0, 0, 283, 1, 0, 0, 0, 0, 285, 1, 0, 0, 0, 0, 287, 1, 0, + 0, 0, 0, 289, 1, 0, 0, 0, 0, 291, 1, 0, 0, 0, 0, 293, 1, 0, 0, 0, 0, 295, 1, 0, 0, 0, 0, 297, + 1, 0, 0, 0, 0, 299, 1, 0, 0, 0, 0, 301, 1, 0, 0, 0, 0, 303, 1, 0, 0, 0, 0, 305, 1, 0, 0, 0, + 0, 307, 1, 0, 0, 0, 0, 309, 1, 0, 0, 0, 0, 311, 1, 0, 0, 0, 0, 313, 1, 0, 0, 0, 0, 315, 1, + 0, 0, 0, 0, 317, 1, 0, 0, 0, 0, 319, 1, 0, 0, 0, 0, 321, 1, 0, 0, 0, 0, 323, 1, 0, 0, 0, 0, + 325, 1, 0, 0, 0, 0, 327, 1, 0, 0, 0, 0, 329, 1, 0, 0, 0, 0, 331, 1, 0, 0, 0, 0, 333, 1, 0, + 0, 0, 0, 335, 1, 0, 0, 0, 0, 337, 1, 0, 0, 0, 0, 339, 1, 0, 0, 0, 0, 341, 1, 0, 0, 0, 0, 343, + 1, 0, 0, 0, 0, 347, 1, 0, 0, 0, 0, 349, 1, 0, 0, 0, 0, 351, 1, 0, 0, 0, 0, 353, 1, 0, 0, 0, + 0, 359, 1, 0, 0, 0, 0, 361, 1, 0, 0, 0, 0, 363, 1, 0, 0, 0, 0, 365, 1, 0, 0, 0, 0, 367, 1, + 0, 0, 0, 0, 369, 1, 0, 0, 0, 0, 371, 1, 0, 0, 0, 0, 373, 1, 0, 0, 0, 0, 375, 1, 0, 0, 0, 0, + 377, 1, 0, 0, 0, 0, 379, 1, 0, 0, 0, 0, 381, 1, 0, 0, 0, 0, 383, 1, 0, 0, 0, 0, 387, 1, 0, + 0, 0, 0, 391, 1, 0, 0, 0, 0, 395, 1, 0, 0, 0, 0, 407, 1, 0, 0, 0, 0, 413, 1, 0, 0, 0, 1, 415, + 1, 0, 0, 0, 3, 422, 1, 0, 0, 0, 5, 427, 1, 0, 0, 0, 7, 437, 1, 0, 0, 0, 9, 444, 1, 0, 0, 0, + 11, 451, 1, 0, 0, 0, 13, 462, 1, 0, 0, 0, 15, 467, 1, 0, 0, 0, 17, 473, 1, 0, 0, 0, 19, 480, + 1, 0, 0, 0, 21, 485, 1, 0, 0, 0, 23, 492, 1, 0, 0, 0, 25, 503, 1, 0, 0, 0, 27, 508, 1, 0, + 0, 0, 29, 524, 1, 0, 0, 0, 31, 528, 1, 0, 0, 0, 33, 540, 1, 0, 0, 0, 35, 546, 1, 0, 0, 0, + 37, 554, 1, 0, 0, 0, 39, 562, 1, 0, 0, 0, 41, 571, 1, 0, 0, 0, 43, 579, 1, 0, 0, 0, 45, 588, + 1, 0, 0, 0, 47, 598, 1, 0, 0, 0, 49, 609, 1, 0, 0, 0, 51, 623, 1, 0, 0, 0, 53, 633, 1, 0, + 0, 0, 55, 644, 1, 0, 0, 0, 57, 656, 1, 0, 0, 0, 59, 664, 1, 0, 0, 0, 61, 674, 1, 0, 0, 0, + 63, 683, 1, 0, 0, 0, 65, 694, 1, 0, 0, 0, 67, 703, 1, 0, 0, 0, 69, 713, 1, 0, 0, 0, 71, 723, + 1, 0, 0, 0, 73, 731, 1, 0, 0, 0, 75, 740, 1, 0, 0, 0, 77, 748, 1, 0, 0, 0, 79, 762, 1, 0, + 0, 0, 81, 770, 1, 0, 0, 0, 83, 773, 1, 0, 0, 0, 85, 778, 1, 0, 0, 0, 87, 786, 1, 0, 0, 0, + 89, 789, 1, 0, 0, 0, 91, 795, 1, 0, 0, 0, 93, 800, 1, 0, 0, 0, 95, 802, 1, 0, 0, 0, 97, 804, + 1, 0, 0, 0, 99, 812, 1, 0, 0, 0, 101, 814, 1, 0, 0, 0, 103, 816, 1, 0, 0, 0, 105, 818, 1, + 0, 0, 0, 107, 826, 1, 0, 0, 0, 109, 834, 1, 0, 0, 0, 111, 836, 1, 0, 0, 0, 113, 838, 1, + 0, 0, 0, 115, 841, 1, 0, 0, 0, 117, 844, 1, 0, 0, 0, 119, 852, 1, 0, 0, 0, 121, 860, 1, + 0, 0, 0, 123, 862, 1, 0, 0, 0, 125, 864, 1, 0, 0, 0, 127, 872, 1, 0, 0, 0, 129, 880, 1, + 0, 0, 0, 131, 882, 1, 0, 0, 0, 133, 889, 1, 0, 0, 0, 135, 896, 1, 0, 0, 0, 137, 902, 1, + 0, 0, 0, 139, 905, 1, 0, 0, 0, 141, 913, 1, 0, 0, 0, 143, 921, 1, 0, 0, 0, 145, 931, 1, + 0, 0, 0, 147, 941, 1, 0, 0, 0, 149, 948, 1, 0, 0, 0, 151, 955, 1, 0, 0, 0, 153, 965, 1, + 0, 0, 0, 155, 975, 1, 0, 0, 0, 157, 981, 1, 0, 0, 0, 159, 988, 1, 0, 0, 0, 161, 995, 1, + 0, 0, 0, 163, 1003, 1, 0, 0, 0, 165, 1063, 1, 0, 0, 0, 167, 1065, 1, 0, 0, 0, 169, 1070, + 1, 0, 0, 0, 171, 1075, 1, 0, 0, 0, 173, 1081, 1, 0, 0, 0, 175, 1086, 1, 0, 0, 0, 177, 1090, + 1, 0, 0, 0, 179, 1095, 1, 0, 0, 0, 181, 1100, 1, 0, 0, 0, 183, 1105, 1, 0, 0, 0, 185, 1110, + 1, 0, 0, 0, 187, 1115, 1, 0, 0, 0, 189, 1120, 1, 0, 0, 0, 191, 1125, 1, 0, 0, 0, 193, 1133, + 1, 0, 0, 0, 195, 1141, 1, 0, 0, 0, 197, 1149, 1, 0, 0, 0, 199, 1157, 1, 0, 0, 0, 201, 1165, + 1, 0, 0, 0, 203, 1173, 1, 0, 0, 0, 205, 1179, 1, 0, 0, 0, 207, 1185, 1, 0, 0, 0, 209, 1191, + 1, 0, 0, 0, 211, 1199, 1, 0, 0, 0, 213, 1207, 1, 0, 0, 0, 215, 1215, 1, 0, 0, 0, 217, 1224, + 1, 0, 0, 0, 219, 1233, 1, 0, 0, 0, 221, 1242, 1, 0, 0, 0, 223, 1249, 1, 0, 0, 0, 225, 1257, + 1, 0, 0, 0, 227, 1264, 1, 0, 0, 0, 229, 1272, 1, 0, 0, 0, 231, 1279, 1, 0, 0, 0, 233, 1287, + 1, 0, 0, 0, 235, 1291, 1, 0, 0, 0, 237, 1295, 1, 0, 0, 0, 239, 1301, 1, 0, 0, 0, 241, 1306, + 1, 0, 0, 0, 243, 1312, 1, 0, 0, 0, 245, 1317, 1, 0, 0, 0, 247, 1322, 1, 0, 0, 0, 249, 1329, + 1, 0, 0, 0, 251, 1335, 1, 0, 0, 0, 253, 1340, 1, 0, 0, 0, 255, 1345, 1, 0, 0, 0, 257, 1350, + 1, 0, 0, 0, 259, 1354, 1, 0, 0, 0, 261, 1360, 1, 0, 0, 0, 263, 1365, 1, 0, 0, 0, 265, 1370, + 1, 0, 0, 0, 267, 1375, 1, 0, 0, 0, 269, 1380, 1, 0, 0, 0, 271, 1385, 1, 0, 0, 0, 273, 1397, + 1, 0, 0, 0, 275, 1399, 1, 0, 0, 0, 277, 1404, 1, 0, 0, 0, 279, 1411, 1, 0, 0, 0, 281, 1450, + 1, 0, 0, 0, 283, 1452, 1, 0, 0, 0, 285, 1481, 1, 0, 0, 0, 287, 1503, 1, 0, 0, 0, 289, 1527, + 1, 0, 0, 0, 291, 1535, 1, 0, 0, 0, 293, 1537, 1, 0, 0, 0, 295, 1544, 1, 0, 0, 0, 297, 1550, + 1, 0, 0, 0, 299, 1555, 1, 0, 0, 0, 301, 1581, 1, 0, 0, 0, 303, 1583, 1, 0, 0, 0, 305, 1591, + 1, 0, 0, 0, 307, 1596, 1, 0, 0, 0, 309, 1604, 1, 0, 0, 0, 311, 1618, 1, 0, 0, 0, 313, 1625, + 1, 0, 0, 0, 315, 1633, 1, 0, 0, 0, 317, 1641, 1, 0, 0, 0, 319, 1652, 1, 0, 0, 0, 321, 1654, + 1, 0, 0, 0, 323, 1665, 1, 0, 0, 0, 325, 1674, 1, 0, 0, 0, 327, 1685, 1, 0, 0, 0, 329, 1694, + 1, 0, 0, 0, 331, 1696, 1, 0, 0, 0, 333, 1699, 1, 0, 0, 0, 335, 1701, 1, 0, 0, 0, 337, 1703, + 1, 0, 0, 0, 339, 1705, 1, 0, 0, 0, 341, 1707, 1, 0, 0, 0, 343, 1709, 1, 0, 0, 0, 345, 1711, + 1, 0, 0, 0, 347, 1713, 1, 0, 0, 0, 349, 1743, 1, 0, 0, 0, 351, 1745, 1, 0, 0, 0, 353, 1747, + 1, 0, 0, 0, 355, 1749, 1, 0, 0, 0, 357, 1751, 1, 0, 0, 0, 359, 1777, 1, 0, 0, 0, 361, 1815, + 1, 0, 0, 0, 363, 1854, 1, 0, 0, 0, 365, 1856, 1, 0, 0, 0, 367, 1867, 1, 0, 0, 0, 369, 1871, + 1, 0, 0, 0, 371, 1881, 1, 0, 0, 0, 373, 1883, 1, 0, 0, 0, 375, 1901, 1, 0, 0, 0, 377, 1903, + 1, 0, 0, 0, 379, 1921, 1, 0, 0, 0, 381, 1945, 1, 0, 0, 0, 383, 1947, 1, 0, 0, 0, 385, 1949, + 1, 0, 0, 0, 387, 1952, 1, 0, 0, 0, 389, 2340, 1, 0, 0, 0, 391, 2342, 1, 0, 0, 0, 393, 2696, + 1, 0, 0, 0, 395, 2698, 1, 0, 0, 0, 397, 2702, 1, 0, 0, 0, 399, 2706, 1, 0, 0, 0, 401, 2713, + 1, 0, 0, 0, 403, 2729, 1, 0, 0, 0, 405, 2731, 1, 0, 0, 0, 407, 2745, 1, 0, 0, 0, 409, 2747, + 1, 0, 0, 0, 411, 2761, 1, 0, 0, 0, 413, 2788, 1, 0, 0, 0, 415, 416, 5, 92, 0, 0, 416, 417, + 5, 97, 0, 0, 417, 418, 5, 99, 0, 0, 418, 419, 5, 117, 0, 0, 419, 420, 5, 116, 0, 0, 420, + 421, 5, 101, 0, 0, 421, 2, 1, 0, 0, 0, 422, 423, 5, 92, 0, 0, 423, 424, 5, 98, 0, 0, 424, + 425, 5, 97, 0, 0, 425, 426, 5, 114, 0, 0, 426, 4, 1, 0, 0, 0, 427, 428, 5, 92, 0, 0, 428, + 429, 5, 111, 0, 0, 429, 430, 5, 118, 0, 0, 430, 431, 5, 101, 0, 0, 431, 432, 5, 114, + 0, 0, 432, 433, 5, 108, 0, 0, 433, 434, 5, 105, 0, 0, 434, 435, 5, 110, 0, 0, 435, 436, + 5, 101, 0, 0, 436, 6, 1, 0, 0, 0, 437, 438, 5, 92, 0, 0, 438, 439, 5, 98, 0, 0, 439, 440, + 5, 114, 0, 0, 440, 441, 5, 101, 0, 0, 441, 442, 5, 118, 0, 0, 442, 443, 5, 101, 0, 0, + 443, 8, 1, 0, 0, 0, 444, 445, 5, 92, 0, 0, 445, 446, 5, 99, 0, 0, 446, 447, 5, 104, 0, + 0, 447, 448, 5, 101, 0, 0, 448, 449, 5, 99, 0, 0, 449, 450, 5, 107, 0, 0, 450, 10, 1, + 0, 0, 0, 451, 452, 5, 92, 0, 0, 452, 453, 5, 119, 0, 0, 453, 454, 5, 105, 0, 0, 454, 455, + 5, 100, 0, 0, 455, 456, 5, 101, 0, 0, 456, 457, 5, 99, 0, 0, 457, 458, 5, 104, 0, 0, 458, + 459, 5, 101, 0, 0, 459, 460, 5, 99, 0, 0, 460, 461, 5, 107, 0, 0, 461, 12, 1, 0, 0, 0, + 462, 463, 5, 92, 0, 0, 463, 464, 5, 100, 0, 0, 464, 465, 5, 111, 0, 0, 465, 466, 5, 116, + 0, 0, 466, 14, 1, 0, 0, 0, 467, 468, 5, 92, 0, 0, 468, 469, 5, 100, 0, 0, 469, 470, 5, + 100, 0, 0, 470, 471, 5, 111, 0, 0, 471, 472, 5, 116, 0, 0, 472, 16, 1, 0, 0, 0, 473, 474, + 5, 92, 0, 0, 474, 475, 5, 103, 0, 0, 475, 476, 5, 114, 0, 0, 476, 477, 5, 97, 0, 0, 477, + 478, 5, 118, 0, 0, 478, 479, 5, 101, 0, 0, 479, 18, 1, 0, 0, 0, 480, 481, 5, 92, 0, 0, + 481, 482, 5, 104, 0, 0, 482, 483, 5, 97, 0, 0, 483, 484, 5, 116, 0, 0, 484, 20, 1, 0, + 0, 0, 485, 486, 5, 92, 0, 0, 486, 487, 5, 116, 0, 0, 487, 488, 5, 105, 0, 0, 488, 489, + 5, 108, 0, 0, 489, 490, 5, 100, 0, 0, 490, 491, 5, 101, 0, 0, 491, 22, 1, 0, 0, 0, 492, + 493, 5, 92, 0, 0, 493, 494, 5, 119, 0, 0, 494, 495, 5, 105, 0, 0, 495, 496, 5, 100, 0, + 0, 496, 497, 5, 101, 0, 0, 497, 498, 5, 116, 0, 0, 498, 499, 5, 105, 0, 0, 499, 500, + 5, 108, 0, 0, 500, 501, 5, 100, 0, 0, 501, 502, 5, 101, 0, 0, 502, 24, 1, 0, 0, 0, 503, + 504, 5, 92, 0, 0, 504, 505, 5, 118, 0, 0, 505, 506, 5, 101, 0, 0, 506, 507, 5, 99, 0, + 0, 507, 26, 1, 0, 0, 0, 508, 509, 5, 92, 0, 0, 509, 510, 5, 111, 0, 0, 510, 511, 5, 118, + 0, 0, 511, 512, 5, 101, 0, 0, 512, 513, 5, 114, 0, 0, 513, 514, 5, 114, 0, 0, 514, 515, + 5, 105, 0, 0, 515, 516, 5, 103, 0, 0, 516, 517, 5, 104, 0, 0, 517, 518, 5, 116, 0, 0, + 518, 519, 5, 97, 0, 0, 519, 520, 5, 114, 0, 0, 520, 521, 5, 114, 0, 0, 521, 522, 5, 111, + 0, 0, 522, 523, 5, 119, 0, 0, 523, 28, 1, 0, 0, 0, 524, 525, 5, 92, 0, 0, 525, 526, 5, + 98, 0, 0, 526, 527, 5, 109, 0, 0, 527, 30, 1, 0, 0, 0, 528, 529, 5, 92, 0, 0, 529, 530, + 5, 98, 0, 0, 530, 531, 5, 111, 0, 0, 531, 532, 5, 108, 0, 0, 532, 533, 5, 100, 0, 0, 533, + 534, 5, 115, 0, 0, 534, 535, 5, 121, 0, 0, 535, 536, 5, 109, 0, 0, 536, 537, 5, 98, 0, + 0, 537, 538, 5, 111, 0, 0, 538, 539, 5, 108, 0, 0, 539, 32, 1, 0, 0, 0, 540, 541, 5, 92, + 0, 0, 541, 542, 5, 116, 0, 0, 542, 543, 5, 101, 0, 0, 543, 544, 5, 120, 0, 0, 544, 545, + 5, 116, 0, 0, 545, 34, 1, 0, 0, 0, 546, 547, 5, 92, 0, 0, 547, 548, 5, 116, 0, 0, 548, + 549, 5, 101, 0, 0, 549, 550, 5, 120, 0, 0, 550, 551, 5, 116, 0, 0, 551, 552, 5, 105, + 0, 0, 552, 553, 5, 116, 0, 0, 553, 36, 1, 0, 0, 0, 554, 555, 5, 92, 0, 0, 555, 556, 5, + 109, 0, 0, 556, 557, 5, 97, 0, 0, 557, 558, 5, 116, 0, 0, 558, 559, 5, 104, 0, 0, 559, + 560, 5, 98, 0, 0, 560, 561, 5, 98, 0, 0, 561, 38, 1, 0, 0, 0, 562, 563, 5, 92, 0, 0, 563, + 564, 5, 109, 0, 0, 564, 565, 5, 97, 0, 0, 565, 566, 5, 116, 0, 0, 566, 567, 5, 104, 0, + 0, 567, 568, 5, 98, 0, 0, 568, 569, 5, 105, 0, 0, 569, 570, 5, 110, 0, 0, 570, 40, 1, + 0, 0, 0, 571, 572, 5, 92, 0, 0, 572, 573, 5, 109, 0, 0, 573, 574, 5, 97, 0, 0, 574, 575, + 5, 116, 0, 0, 575, 576, 5, 104, 0, 0, 576, 577, 5, 98, 0, 0, 577, 578, 5, 102, 0, 0, 578, + 42, 1, 0, 0, 0, 579, 580, 5, 92, 0, 0, 580, 581, 5, 109, 0, 0, 581, 582, 5, 97, 0, 0, 582, + 583, 5, 116, 0, 0, 583, 584, 5, 104, 0, 0, 584, 585, 5, 99, 0, 0, 585, 586, 5, 97, 0, + 0, 586, 587, 5, 108, 0, 0, 587, 44, 1, 0, 0, 0, 588, 589, 5, 92, 0, 0, 589, 590, 5, 109, + 0, 0, 590, 591, 5, 97, 0, 0, 591, 592, 5, 116, 0, 0, 592, 593, 5, 104, 0, 0, 593, 594, + 5, 99, 0, 0, 594, 595, 5, 108, 0, 0, 595, 596, 5, 97, 0, 0, 596, 597, 5, 112, 0, 0, 597, + 46, 1, 0, 0, 0, 598, 599, 5, 92, 0, 0, 599, 600, 5, 109, 0, 0, 600, 601, 5, 97, 0, 0, 601, + 602, 5, 116, 0, 0, 602, 603, 5, 104, 0, 0, 603, 604, 5, 99, 0, 0, 604, 605, 5, 108, 0, + 0, 605, 606, 5, 111, 0, 0, 606, 607, 5, 115, 0, 0, 607, 608, 5, 101, 0, 0, 608, 48, 1, + 0, 0, 0, 609, 610, 5, 92, 0, 0, 610, 611, 5, 109, 0, 0, 611, 612, 5, 97, 0, 0, 612, 613, + 5, 116, 0, 0, 613, 614, 5, 104, 0, 0, 614, 615, 5, 101, 0, 0, 615, 616, 5, 108, 0, 0, + 616, 617, 5, 108, 0, 0, 617, 618, 5, 105, 0, 0, 618, 619, 5, 112, 0, 0, 619, 620, 5, + 115, 0, 0, 620, 621, 5, 105, 0, 0, 621, 622, 5, 115, 0, 0, 622, 50, 1, 0, 0, 0, 623, 624, + 5, 92, 0, 0, 624, 625, 5, 109, 0, 0, 625, 626, 5, 97, 0, 0, 626, 627, 5, 116, 0, 0, 627, + 628, 5, 104, 0, 0, 628, 629, 5, 102, 0, 0, 629, 630, 5, 114, 0, 0, 630, 631, 5, 97, 0, + 0, 631, 632, 5, 107, 0, 0, 632, 52, 1, 0, 0, 0, 633, 634, 5, 92, 0, 0, 634, 635, 5, 109, + 0, 0, 635, 636, 5, 97, 0, 0, 636, 637, 5, 116, 0, 0, 637, 638, 5, 104, 0, 0, 638, 639, + 5, 105, 0, 0, 639, 640, 5, 110, 0, 0, 640, 641, 5, 110, 0, 0, 641, 642, 5, 101, 0, 0, + 642, 643, 5, 114, 0, 0, 643, 54, 1, 0, 0, 0, 644, 645, 5, 92, 0, 0, 645, 646, 5, 109, + 0, 0, 646, 647, 5, 97, 0, 0, 647, 648, 5, 116, 0, 0, 648, 649, 5, 104, 0, 0, 649, 650, + 5, 110, 0, 0, 650, 651, 5, 111, 0, 0, 651, 652, 5, 114, 0, 0, 652, 653, 5, 109, 0, 0, + 653, 654, 5, 97, 0, 0, 654, 655, 5, 108, 0, 0, 655, 56, 1, 0, 0, 0, 656, 657, 5, 92, 0, + 0, 657, 658, 5, 109, 0, 0, 658, 659, 5, 97, 0, 0, 659, 660, 5, 116, 0, 0, 660, 661, 5, + 104, 0, 0, 661, 662, 5, 111, 0, 0, 662, 663, 5, 112, 0, 0, 663, 58, 1, 0, 0, 0, 664, 665, + 5, 92, 0, 0, 665, 666, 5, 109, 0, 0, 666, 667, 5, 97, 0, 0, 667, 668, 5, 116, 0, 0, 668, + 669, 5, 104, 0, 0, 669, 670, 5, 111, 0, 0, 670, 671, 5, 112, 0, 0, 671, 672, 5, 101, + 0, 0, 672, 673, 5, 110, 0, 0, 673, 60, 1, 0, 0, 0, 674, 675, 5, 92, 0, 0, 675, 676, 5, + 109, 0, 0, 676, 677, 5, 97, 0, 0, 677, 678, 5, 116, 0, 0, 678, 679, 5, 104, 0, 0, 679, + 680, 5, 111, 0, 0, 680, 681, 5, 114, 0, 0, 681, 682, 5, 100, 0, 0, 682, 62, 1, 0, 0, 0, + 683, 684, 5, 92, 0, 0, 684, 685, 5, 109, 0, 0, 685, 686, 5, 97, 0, 0, 686, 687, 5, 116, + 0, 0, 687, 688, 5, 104, 0, 0, 688, 689, 5, 112, 0, 0, 689, 690, 5, 117, 0, 0, 690, 691, + 5, 110, 0, 0, 691, 692, 5, 99, 0, 0, 692, 693, 5, 116, 0, 0, 693, 64, 1, 0, 0, 0, 694, + 695, 5, 92, 0, 0, 695, 696, 5, 109, 0, 0, 696, 697, 5, 97, 0, 0, 697, 698, 5, 116, 0, + 0, 698, 699, 5, 104, 0, 0, 699, 700, 5, 114, 0, 0, 700, 701, 5, 101, 0, 0, 701, 702, + 5, 108, 0, 0, 702, 66, 1, 0, 0, 0, 703, 704, 5, 92, 0, 0, 704, 705, 5, 109, 0, 0, 705, + 706, 5, 97, 0, 0, 706, 707, 5, 116, 0, 0, 707, 708, 5, 104, 0, 0, 708, 709, 5, 114, 0, + 0, 709, 710, 5, 105, 0, 0, 710, 711, 5, 110, 0, 0, 711, 712, 5, 103, 0, 0, 712, 68, 1, + 0, 0, 0, 713, 714, 5, 92, 0, 0, 714, 715, 5, 109, 0, 0, 715, 716, 5, 97, 0, 0, 716, 717, + 5, 116, 0, 0, 717, 718, 5, 104, 0, 0, 718, 719, 5, 114, 0, 0, 719, 720, 5, 108, 0, 0, + 720, 721, 5, 97, 0, 0, 721, 722, 5, 112, 0, 0, 722, 70, 1, 0, 0, 0, 723, 724, 5, 92, 0, + 0, 724, 725, 5, 109, 0, 0, 725, 726, 5, 97, 0, 0, 726, 727, 5, 116, 0, 0, 727, 728, 5, + 104, 0, 0, 728, 729, 5, 114, 0, 0, 729, 730, 5, 109, 0, 0, 730, 72, 1, 0, 0, 0, 731, 732, + 5, 92, 0, 0, 732, 733, 5, 109, 0, 0, 733, 734, 5, 97, 0, 0, 734, 735, 5, 116, 0, 0, 735, + 736, 5, 104, 0, 0, 736, 737, 5, 115, 0, 0, 737, 738, 5, 99, 0, 0, 738, 739, 5, 114, 0, + 0, 739, 74, 1, 0, 0, 0, 740, 741, 5, 92, 0, 0, 741, 742, 5, 109, 0, 0, 742, 743, 5, 97, + 0, 0, 743, 744, 5, 116, 0, 0, 744, 745, 5, 104, 0, 0, 745, 746, 5, 115, 0, 0, 746, 747, + 5, 102, 0, 0, 747, 76, 1, 0, 0, 0, 748, 749, 5, 92, 0, 0, 749, 750, 5, 109, 0, 0, 750, + 751, 5, 97, 0, 0, 751, 752, 5, 116, 0, 0, 752, 753, 5, 104, 0, 0, 753, 754, 5, 115, 0, + 0, 754, 755, 5, 116, 0, 0, 755, 756, 5, 101, 0, 0, 756, 757, 5, 114, 0, 0, 757, 758, + 5, 108, 0, 0, 758, 759, 5, 105, 0, 0, 759, 760, 5, 110, 0, 0, 760, 761, 5, 103, 0, 0, + 761, 78, 1, 0, 0, 0, 762, 763, 5, 92, 0, 0, 763, 764, 5, 109, 0, 0, 764, 765, 5, 97, 0, + 0, 765, 766, 5, 116, 0, 0, 766, 767, 5, 104, 0, 0, 767, 768, 5, 116, 0, 0, 768, 769, + 5, 116, 0, 0, 769, 80, 1, 0, 0, 0, 770, 771, 5, 94, 0, 0, 771, 772, 5, 84, 0, 0, 772, 82, + 1, 0, 0, 0, 773, 774, 5, 94, 0, 0, 774, 775, 5, 123, 0, 0, 775, 776, 5, 84, 0, 0, 776, + 777, 5, 125, 0, 0, 777, 84, 1, 0, 0, 0, 778, 779, 5, 94, 0, 0, 779, 780, 5, 123, 0, 0, + 780, 781, 5, 92, 0, 0, 781, 782, 5, 116, 0, 0, 782, 783, 5, 111, 0, 0, 783, 784, 5, 112, + 0, 0, 784, 785, 5, 125, 0, 0, 785, 86, 1, 0, 0, 0, 786, 787, 5, 39, 0, 0, 787, 88, 1, 0, + 0, 0, 788, 790, 7, 0, 0, 0, 789, 788, 1, 0, 0, 0, 790, 791, 1, 0, 0, 0, 791, 789, 1, 0, + 0, 0, 791, 792, 1, 0, 0, 0, 792, 793, 1, 0, 0, 0, 793, 794, 6, 44, 0, 0, 794, 90, 1, 0, + 0, 0, 795, 796, 5, 92, 0, 0, 796, 797, 5, 36, 0, 0, 797, 798, 1, 0, 0, 0, 798, 799, 6, + 45, 0, 0, 799, 92, 1, 0, 0, 0, 800, 801, 5, 43, 0, 0, 801, 94, 1, 0, 0, 0, 802, 803, 5, + 45, 0, 0, 803, 96, 1, 0, 0, 0, 804, 805, 5, 42, 0, 0, 805, 98, 1, 0, 0, 0, 806, 813, 5, + 47, 0, 0, 807, 808, 5, 92, 0, 0, 808, 809, 5, 111, 0, 0, 809, 810, 5, 118, 0, 0, 810, + 811, 5, 101, 0, 0, 811, 813, 5, 114, 0, 0, 812, 806, 1, 0, 0, 0, 812, 807, 1, 0, 0, 0, + 813, 100, 1, 0, 0, 0, 814, 815, 5, 40, 0, 0, 815, 102, 1, 0, 0, 0, 816, 817, 5, 41, 0, + 0, 817, 104, 1, 0, 0, 0, 818, 819, 5, 92, 0, 0, 819, 820, 5, 108, 0, 0, 820, 821, 5, 103, + 0, 0, 821, 822, 5, 114, 0, 0, 822, 823, 5, 111, 0, 0, 823, 824, 5, 117, 0, 0, 824, 825, + 5, 112, 0, 0, 825, 106, 1, 0, 0, 0, 826, 827, 5, 92, 0, 0, 827, 828, 5, 114, 0, 0, 828, + 829, 5, 103, 0, 0, 829, 830, 5, 114, 0, 0, 830, 831, 5, 111, 0, 0, 831, 832, 5, 117, + 0, 0, 832, 833, 5, 112, 0, 0, 833, 108, 1, 0, 0, 0, 834, 835, 5, 123, 0, 0, 835, 110, + 1, 0, 0, 0, 836, 837, 5, 125, 0, 0, 837, 112, 1, 0, 0, 0, 838, 839, 5, 92, 0, 0, 839, 840, + 5, 123, 0, 0, 840, 114, 1, 0, 0, 0, 841, 842, 5, 92, 0, 0, 842, 843, 5, 125, 0, 0, 843, + 116, 1, 0, 0, 0, 844, 845, 5, 92, 0, 0, 845, 846, 5, 108, 0, 0, 846, 847, 5, 98, 0, 0, + 847, 848, 5, 114, 0, 0, 848, 849, 5, 97, 0, 0, 849, 850, 5, 99, 0, 0, 850, 851, 5, 101, + 0, 0, 851, 118, 1, 0, 0, 0, 852, 853, 5, 92, 0, 0, 853, 854, 5, 114, 0, 0, 854, 855, 5, + 98, 0, 0, 855, 856, 5, 114, 0, 0, 856, 857, 5, 97, 0, 0, 857, 858, 5, 99, 0, 0, 858, 859, + 5, 101, 0, 0, 859, 120, 1, 0, 0, 0, 860, 861, 5, 91, 0, 0, 861, 122, 1, 0, 0, 0, 862, 863, + 5, 93, 0, 0, 863, 124, 1, 0, 0, 0, 864, 865, 5, 92, 0, 0, 865, 866, 5, 108, 0, 0, 866, + 867, 5, 98, 0, 0, 867, 868, 5, 114, 0, 0, 868, 869, 5, 97, 0, 0, 869, 870, 5, 99, 0, 0, + 870, 871, 5, 107, 0, 0, 871, 126, 1, 0, 0, 0, 872, 873, 5, 92, 0, 0, 873, 874, 5, 114, + 0, 0, 874, 875, 5, 98, 0, 0, 875, 876, 5, 114, 0, 0, 876, 877, 5, 97, 0, 0, 877, 878, + 5, 99, 0, 0, 878, 879, 5, 107, 0, 0, 879, 128, 1, 0, 0, 0, 880, 881, 5, 124, 0, 0, 881, + 130, 1, 0, 0, 0, 882, 883, 5, 92, 0, 0, 883, 884, 5, 108, 0, 0, 884, 885, 5, 118, 0, 0, + 885, 886, 5, 101, 0, 0, 886, 887, 5, 114, 0, 0, 887, 888, 5, 116, 0, 0, 888, 132, 1, + 0, 0, 0, 889, 890, 5, 92, 0, 0, 890, 891, 5, 114, 0, 0, 891, 892, 5, 118, 0, 0, 892, 893, + 5, 101, 0, 0, 893, 894, 5, 114, 0, 0, 894, 895, 5, 116, 0, 0, 895, 134, 1, 0, 0, 0, 896, + 897, 5, 92, 0, 0, 897, 898, 5, 118, 0, 0, 898, 899, 5, 101, 0, 0, 899, 900, 5, 114, 0, + 0, 900, 901, 5, 116, 0, 0, 901, 136, 1, 0, 0, 0, 902, 903, 5, 92, 0, 0, 903, 904, 5, 124, + 0, 0, 904, 138, 1, 0, 0, 0, 905, 906, 5, 92, 0, 0, 906, 907, 5, 108, 0, 0, 907, 908, 5, + 102, 0, 0, 908, 909, 5, 108, 0, 0, 909, 910, 5, 111, 0, 0, 910, 911, 5, 111, 0, 0, 911, + 912, 5, 114, 0, 0, 912, 140, 1, 0, 0, 0, 913, 914, 5, 92, 0, 0, 914, 915, 5, 114, 0, 0, + 915, 916, 5, 102, 0, 0, 916, 917, 5, 108, 0, 0, 917, 918, 5, 111, 0, 0, 918, 919, 5, + 111, 0, 0, 919, 920, 5, 114, 0, 0, 920, 142, 1, 0, 0, 0, 921, 922, 5, 92, 0, 0, 922, 923, + 5, 108, 0, 0, 923, 924, 5, 108, 0, 0, 924, 925, 5, 99, 0, 0, 925, 926, 5, 111, 0, 0, 926, + 927, 5, 114, 0, 0, 927, 928, 5, 110, 0, 0, 928, 929, 5, 101, 0, 0, 929, 930, 5, 114, + 0, 0, 930, 144, 1, 0, 0, 0, 931, 932, 5, 92, 0, 0, 932, 933, 5, 108, 0, 0, 933, 934, 5, + 114, 0, 0, 934, 935, 5, 99, 0, 0, 935, 936, 5, 111, 0, 0, 936, 937, 5, 114, 0, 0, 937, + 938, 5, 110, 0, 0, 938, 939, 5, 101, 0, 0, 939, 940, 5, 114, 0, 0, 940, 146, 1, 0, 0, + 0, 941, 942, 5, 92, 0, 0, 942, 943, 5, 108, 0, 0, 943, 944, 5, 99, 0, 0, 944, 945, 5, + 101, 0, 0, 945, 946, 5, 105, 0, 0, 946, 947, 5, 108, 0, 0, 947, 148, 1, 0, 0, 0, 948, + 949, 5, 92, 0, 0, 949, 950, 5, 114, 0, 0, 950, 951, 5, 99, 0, 0, 951, 952, 5, 101, 0, + 0, 952, 953, 5, 105, 0, 0, 953, 954, 5, 108, 0, 0, 954, 150, 1, 0, 0, 0, 955, 956, 5, + 92, 0, 0, 956, 957, 5, 117, 0, 0, 957, 958, 5, 108, 0, 0, 958, 959, 5, 99, 0, 0, 959, + 960, 5, 111, 0, 0, 960, 961, 5, 114, 0, 0, 961, 962, 5, 110, 0, 0, 962, 963, 5, 101, + 0, 0, 963, 964, 5, 114, 0, 0, 964, 152, 1, 0, 0, 0, 965, 966, 5, 92, 0, 0, 966, 967, 5, + 117, 0, 0, 967, 968, 5, 114, 0, 0, 968, 969, 5, 99, 0, 0, 969, 970, 5, 111, 0, 0, 970, + 971, 5, 114, 0, 0, 971, 972, 5, 110, 0, 0, 972, 973, 5, 101, 0, 0, 973, 974, 5, 114, + 0, 0, 974, 154, 1, 0, 0, 0, 975, 976, 5, 92, 0, 0, 976, 977, 5, 108, 0, 0, 977, 978, 5, + 101, 0, 0, 978, 979, 5, 102, 0, 0, 979, 980, 5, 116, 0, 0, 980, 156, 1, 0, 0, 0, 981, + 982, 5, 92, 0, 0, 982, 983, 5, 114, 0, 0, 983, 984, 5, 105, 0, 0, 984, 985, 5, 103, 0, + 0, 985, 986, 5, 104, 0, 0, 986, 987, 5, 116, 0, 0, 987, 158, 1, 0, 0, 0, 988, 989, 5, + 92, 0, 0, 989, 990, 5, 109, 0, 0, 990, 991, 5, 108, 0, 0, 991, 992, 5, 101, 0, 0, 992, + 993, 5, 102, 0, 0, 993, 994, 5, 116, 0, 0, 994, 160, 1, 0, 0, 0, 995, 996, 5, 92, 0, 0, + 996, 997, 5, 109, 0, 0, 997, 998, 5, 114, 0, 0, 998, 999, 5, 105, 0, 0, 999, 1000, 5, + 103, 0, 0, 1000, 1001, 5, 104, 0, 0, 1001, 1002, 5, 116, 0, 0, 1002, 162, 1, 0, 0, 0, + 1003, 1004, 5, 92, 0, 0, 1004, 1005, 5, 108, 0, 0, 1005, 1006, 5, 105, 0, 0, 1006, + 1007, 5, 109, 0, 0, 1007, 164, 1, 0, 0, 0, 1008, 1009, 5, 92, 0, 0, 1009, 1010, 5, 116, + 0, 0, 1010, 1064, 5, 111, 0, 0, 1011, 1012, 5, 92, 0, 0, 1012, 1013, 5, 114, 0, 0, 1013, + 1014, 5, 105, 0, 0, 1014, 1015, 5, 103, 0, 0, 1015, 1016, 5, 104, 0, 0, 1016, 1017, + 5, 116, 0, 0, 1017, 1018, 5, 97, 0, 0, 1018, 1019, 5, 114, 0, 0, 1019, 1020, 5, 114, + 0, 0, 1020, 1021, 5, 111, 0, 0, 1021, 1064, 5, 119, 0, 0, 1022, 1023, 5, 92, 0, 0, 1023, + 1024, 5, 82, 0, 0, 1024, 1025, 5, 105, 0, 0, 1025, 1026, 5, 103, 0, 0, 1026, 1027, + 5, 104, 0, 0, 1027, 1028, 5, 116, 0, 0, 1028, 1029, 5, 97, 0, 0, 1029, 1030, 5, 114, + 0, 0, 1030, 1031, 5, 114, 0, 0, 1031, 1032, 5, 111, 0, 0, 1032, 1064, 5, 119, 0, 0, + 1033, 1034, 5, 92, 0, 0, 1034, 1035, 5, 108, 0, 0, 1035, 1036, 5, 111, 0, 0, 1036, + 1037, 5, 110, 0, 0, 1037, 1038, 5, 103, 0, 0, 1038, 1039, 5, 114, 0, 0, 1039, 1040, + 5, 105, 0, 0, 1040, 1041, 5, 103, 0, 0, 1041, 1042, 5, 104, 0, 0, 1042, 1043, 5, 116, + 0, 0, 1043, 1044, 5, 97, 0, 0, 1044, 1045, 5, 114, 0, 0, 1045, 1046, 5, 114, 0, 0, 1046, + 1047, 5, 111, 0, 0, 1047, 1064, 5, 119, 0, 0, 1048, 1049, 5, 92, 0, 0, 1049, 1050, + 5, 76, 0, 0, 1050, 1051, 5, 111, 0, 0, 1051, 1052, 5, 110, 0, 0, 1052, 1053, 5, 103, + 0, 0, 1053, 1054, 5, 114, 0, 0, 1054, 1055, 5, 105, 0, 0, 1055, 1056, 5, 103, 0, 0, + 1056, 1057, 5, 104, 0, 0, 1057, 1058, 5, 116, 0, 0, 1058, 1059, 5, 97, 0, 0, 1059, + 1060, 5, 114, 0, 0, 1060, 1061, 5, 114, 0, 0, 1061, 1062, 5, 111, 0, 0, 1062, 1064, + 5, 119, 0, 0, 1063, 1008, 1, 0, 0, 0, 1063, 1011, 1, 0, 0, 0, 1063, 1022, 1, 0, 0, 0, + 1063, 1033, 1, 0, 0, 0, 1063, 1048, 1, 0, 0, 0, 1064, 166, 1, 0, 0, 0, 1065, 1066, 5, + 92, 0, 0, 1066, 1067, 5, 105, 0, 0, 1067, 1068, 5, 110, 0, 0, 1068, 1069, 5, 116, 0, + 0, 1069, 168, 1, 0, 0, 0, 1070, 1071, 5, 92, 0, 0, 1071, 1072, 5, 115, 0, 0, 1072, 1073, + 5, 117, 0, 0, 1073, 1074, 5, 109, 0, 0, 1074, 170, 1, 0, 0, 0, 1075, 1076, 5, 92, 0, + 0, 1076, 1077, 5, 112, 0, 0, 1077, 1078, 5, 114, 0, 0, 1078, 1079, 5, 111, 0, 0, 1079, + 1080, 5, 100, 0, 0, 1080, 172, 1, 0, 0, 0, 1081, 1082, 5, 92, 0, 0, 1082, 1083, 5, 108, + 0, 0, 1083, 1084, 5, 111, 0, 0, 1084, 1085, 5, 103, 0, 0, 1085, 174, 1, 0, 0, 0, 1086, + 1087, 5, 92, 0, 0, 1087, 1088, 5, 108, 0, 0, 1088, 1089, 5, 110, 0, 0, 1089, 176, 1, + 0, 0, 0, 1090, 1091, 5, 92, 0, 0, 1091, 1092, 5, 101, 0, 0, 1092, 1093, 5, 120, 0, 0, + 1093, 1094, 5, 112, 0, 0, 1094, 178, 1, 0, 0, 0, 1095, 1096, 5, 92, 0, 0, 1096, 1097, + 5, 115, 0, 0, 1097, 1098, 5, 105, 0, 0, 1098, 1099, 5, 110, 0, 0, 1099, 180, 1, 0, 0, + 0, 1100, 1101, 5, 92, 0, 0, 1101, 1102, 5, 99, 0, 0, 1102, 1103, 5, 111, 0, 0, 1103, + 1104, 5, 115, 0, 0, 1104, 182, 1, 0, 0, 0, 1105, 1106, 5, 92, 0, 0, 1106, 1107, 5, 116, + 0, 0, 1107, 1108, 5, 97, 0, 0, 1108, 1109, 5, 110, 0, 0, 1109, 184, 1, 0, 0, 0, 1110, + 1111, 5, 92, 0, 0, 1111, 1112, 5, 99, 0, 0, 1112, 1113, 5, 115, 0, 0, 1113, 1114, 5, + 99, 0, 0, 1114, 186, 1, 0, 0, 0, 1115, 1116, 5, 92, 0, 0, 1116, 1117, 5, 115, 0, 0, 1117, + 1118, 5, 101, 0, 0, 1118, 1119, 5, 99, 0, 0, 1119, 188, 1, 0, 0, 0, 1120, 1121, 5, 92, + 0, 0, 1121, 1122, 5, 99, 0, 0, 1122, 1123, 5, 111, 0, 0, 1123, 1124, 5, 116, 0, 0, 1124, + 190, 1, 0, 0, 0, 1125, 1126, 5, 92, 0, 0, 1126, 1127, 5, 97, 0, 0, 1127, 1128, 5, 114, + 0, 0, 1128, 1129, 5, 99, 0, 0, 1129, 1130, 5, 115, 0, 0, 1130, 1131, 5, 105, 0, 0, 1131, + 1132, 5, 110, 0, 0, 1132, 192, 1, 0, 0, 0, 1133, 1134, 5, 92, 0, 0, 1134, 1135, 5, 97, + 0, 0, 1135, 1136, 5, 114, 0, 0, 1136, 1137, 5, 99, 0, 0, 1137, 1138, 5, 99, 0, 0, 1138, + 1139, 5, 111, 0, 0, 1139, 1140, 5, 115, 0, 0, 1140, 194, 1, 0, 0, 0, 1141, 1142, 5, + 92, 0, 0, 1142, 1143, 5, 97, 0, 0, 1143, 1144, 5, 114, 0, 0, 1144, 1145, 5, 99, 0, 0, + 1145, 1146, 5, 116, 0, 0, 1146, 1147, 5, 97, 0, 0, 1147, 1148, 5, 110, 0, 0, 1148, + 196, 1, 0, 0, 0, 1149, 1150, 5, 92, 0, 0, 1150, 1151, 5, 97, 0, 0, 1151, 1152, 5, 114, + 0, 0, 1152, 1153, 5, 99, 0, 0, 1153, 1154, 5, 99, 0, 0, 1154, 1155, 5, 115, 0, 0, 1155, + 1156, 5, 99, 0, 0, 1156, 198, 1, 0, 0, 0, 1157, 1158, 5, 92, 0, 0, 1158, 1159, 5, 97, + 0, 0, 1159, 1160, 5, 114, 0, 0, 1160, 1161, 5, 99, 0, 0, 1161, 1162, 5, 115, 0, 0, 1162, + 1163, 5, 101, 0, 0, 1163, 1164, 5, 99, 0, 0, 1164, 200, 1, 0, 0, 0, 1165, 1166, 5, 92, + 0, 0, 1166, 1167, 5, 97, 0, 0, 1167, 1168, 5, 114, 0, 0, 1168, 1169, 5, 99, 0, 0, 1169, + 1170, 5, 99, 0, 0, 1170, 1171, 5, 111, 0, 0, 1171, 1172, 5, 116, 0, 0, 1172, 202, 1, + 0, 0, 0, 1173, 1174, 5, 92, 0, 0, 1174, 1175, 5, 115, 0, 0, 1175, 1176, 5, 105, 0, 0, + 1176, 1177, 5, 110, 0, 0, 1177, 1178, 5, 104, 0, 0, 1178, 204, 1, 0, 0, 0, 1179, 1180, + 5, 92, 0, 0, 1180, 1181, 5, 99, 0, 0, 1181, 1182, 5, 111, 0, 0, 1182, 1183, 5, 115, + 0, 0, 1183, 1184, 5, 104, 0, 0, 1184, 206, 1, 0, 0, 0, 1185, 1186, 5, 92, 0, 0, 1186, + 1187, 5, 116, 0, 0, 1187, 1188, 5, 97, 0, 0, 1188, 1189, 5, 110, 0, 0, 1189, 1190, + 5, 104, 0, 0, 1190, 208, 1, 0, 0, 0, 1191, 1192, 5, 92, 0, 0, 1192, 1193, 5, 97, 0, 0, + 1193, 1194, 5, 114, 0, 0, 1194, 1195, 5, 115, 0, 0, 1195, 1196, 5, 105, 0, 0, 1196, + 1197, 5, 110, 0, 0, 1197, 1198, 5, 104, 0, 0, 1198, 210, 1, 0, 0, 0, 1199, 1200, 5, + 92, 0, 0, 1200, 1201, 5, 97, 0, 0, 1201, 1202, 5, 114, 0, 0, 1202, 1203, 5, 99, 0, 0, + 1203, 1204, 5, 111, 0, 0, 1204, 1205, 5, 115, 0, 0, 1205, 1206, 5, 104, 0, 0, 1206, + 212, 1, 0, 0, 0, 1207, 1208, 5, 92, 0, 0, 1208, 1209, 5, 97, 0, 0, 1209, 1210, 5, 114, + 0, 0, 1210, 1211, 5, 116, 0, 0, 1211, 1212, 5, 97, 0, 0, 1212, 1213, 5, 110, 0, 0, 1213, + 1214, 5, 104, 0, 0, 1214, 214, 1, 0, 0, 0, 1215, 1216, 5, 92, 0, 0, 1216, 1217, 5, 97, + 0, 0, 1217, 1218, 5, 114, 0, 0, 1218, 1219, 5, 99, 0, 0, 1219, 1220, 5, 115, 0, 0, 1220, + 1221, 5, 105, 0, 0, 1221, 1222, 5, 110, 0, 0, 1222, 1223, 5, 104, 0, 0, 1223, 216, + 1, 0, 0, 0, 1224, 1225, 5, 92, 0, 0, 1225, 1226, 5, 97, 0, 0, 1226, 1227, 5, 114, 0, + 0, 1227, 1228, 5, 99, 0, 0, 1228, 1229, 5, 99, 0, 0, 1229, 1230, 5, 111, 0, 0, 1230, + 1231, 5, 115, 0, 0, 1231, 1232, 5, 104, 0, 0, 1232, 218, 1, 0, 0, 0, 1233, 1234, 5, + 92, 0, 0, 1234, 1235, 5, 97, 0, 0, 1235, 1236, 5, 114, 0, 0, 1236, 1237, 5, 99, 0, 0, + 1237, 1238, 5, 116, 0, 0, 1238, 1239, 5, 97, 0, 0, 1239, 1240, 5, 110, 0, 0, 1240, + 1241, 5, 104, 0, 0, 1241, 220, 1, 0, 0, 0, 1242, 1243, 5, 97, 0, 0, 1243, 1244, 5, 114, + 0, 0, 1244, 1245, 5, 115, 0, 0, 1245, 1246, 5, 105, 0, 0, 1246, 1247, 5, 110, 0, 0, + 1247, 1248, 5, 104, 0, 0, 1248, 222, 1, 0, 0, 0, 1249, 1250, 5, 97, 0, 0, 1250, 1251, + 5, 114, 0, 0, 1251, 1252, 5, 99, 0, 0, 1252, 1253, 5, 115, 0, 0, 1253, 1254, 5, 105, + 0, 0, 1254, 1255, 5, 110, 0, 0, 1255, 1256, 5, 104, 0, 0, 1256, 224, 1, 0, 0, 0, 1257, + 1258, 5, 97, 0, 0, 1258, 1259, 5, 114, 0, 0, 1259, 1260, 5, 99, 0, 0, 1260, 1261, 5, + 111, 0, 0, 1261, 1262, 5, 115, 0, 0, 1262, 1263, 5, 104, 0, 0, 1263, 226, 1, 0, 0, 0, + 1264, 1265, 5, 97, 0, 0, 1265, 1266, 5, 114, 0, 0, 1266, 1267, 5, 99, 0, 0, 1267, 1268, + 5, 99, 0, 0, 1268, 1269, 5, 111, 0, 0, 1269, 1270, 5, 115, 0, 0, 1270, 1271, 5, 104, + 0, 0, 1271, 228, 1, 0, 0, 0, 1272, 1273, 5, 97, 0, 0, 1273, 1274, 5, 114, 0, 0, 1274, + 1275, 5, 116, 0, 0, 1275, 1276, 5, 97, 0, 0, 1276, 1277, 5, 110, 0, 0, 1277, 1278, + 5, 104, 0, 0, 1278, 230, 1, 0, 0, 0, 1279, 1280, 5, 97, 0, 0, 1280, 1281, 5, 114, 0, + 0, 1281, 1282, 5, 99, 0, 0, 1282, 1283, 5, 116, 0, 0, 1283, 1284, 5, 97, 0, 0, 1284, + 1285, 5, 110, 0, 0, 1285, 1286, 5, 104, 0, 0, 1286, 232, 1, 0, 0, 0, 1287, 1288, 5, + 103, 0, 0, 1288, 1289, 5, 99, 0, 0, 1289, 1290, 5, 100, 0, 0, 1290, 234, 1, 0, 0, 0, + 1291, 1292, 5, 108, 0, 0, 1292, 1293, 5, 99, 0, 0, 1293, 1294, 5, 109, 0, 0, 1294, + 236, 1, 0, 0, 0, 1295, 1296, 5, 102, 0, 0, 1296, 1297, 5, 108, 0, 0, 1297, 1298, 5, + 111, 0, 0, 1298, 1299, 5, 111, 0, 0, 1299, 1300, 5, 114, 0, 0, 1300, 238, 1, 0, 0, 0, + 1301, 1302, 5, 99, 0, 0, 1302, 1303, 5, 101, 0, 0, 1303, 1304, 5, 105, 0, 0, 1304, + 1305, 5, 108, 0, 0, 1305, 240, 1, 0, 0, 0, 1306, 1307, 5, 92, 0, 0, 1307, 1308, 5, 115, + 0, 0, 1308, 1309, 5, 113, 0, 0, 1309, 1310, 5, 114, 0, 0, 1310, 1311, 5, 116, 0, 0, + 1311, 242, 1, 0, 0, 0, 1312, 1313, 5, 92, 0, 0, 1313, 1314, 5, 103, 0, 0, 1314, 1315, + 5, 99, 0, 0, 1315, 1316, 5, 100, 0, 0, 1316, 244, 1, 0, 0, 0, 1317, 1318, 5, 92, 0, 0, + 1318, 1319, 5, 108, 0, 0, 1319, 1320, 5, 99, 0, 0, 1320, 1321, 5, 109, 0, 0, 1321, + 246, 1, 0, 0, 0, 1322, 1323, 5, 92, 0, 0, 1323, 1324, 5, 102, 0, 0, 1324, 1325, 5, 108, + 0, 0, 1325, 1326, 5, 111, 0, 0, 1326, 1327, 5, 111, 0, 0, 1327, 1328, 5, 114, 0, 0, + 1328, 248, 1, 0, 0, 0, 1329, 1330, 5, 92, 0, 0, 1330, 1331, 5, 99, 0, 0, 1331, 1332, + 5, 101, 0, 0, 1332, 1333, 5, 105, 0, 0, 1333, 1334, 5, 108, 0, 0, 1334, 250, 1, 0, 0, + 0, 1335, 1336, 5, 92, 0, 0, 1336, 1337, 5, 109, 0, 0, 1337, 1338, 5, 97, 0, 0, 1338, + 1339, 5, 120, 0, 0, 1339, 252, 1, 0, 0, 0, 1340, 1341, 5, 92, 0, 0, 1341, 1342, 5, 109, + 0, 0, 1342, 1343, 5, 105, 0, 0, 1343, 1344, 5, 110, 0, 0, 1344, 254, 1, 0, 0, 0, 1345, + 1346, 5, 92, 0, 0, 1346, 1347, 5, 100, 0, 0, 1347, 1348, 5, 101, 0, 0, 1348, 1349, + 5, 116, 0, 0, 1349, 256, 1, 0, 0, 0, 1350, 1351, 5, 101, 0, 0, 1351, 1352, 5, 121, 0, + 0, 1352, 1353, 5, 101, 0, 0, 1353, 258, 1, 0, 0, 0, 1354, 1355, 5, 122, 0, 0, 1355, + 1356, 5, 101, 0, 0, 1356, 1357, 5, 114, 0, 0, 1357, 1358, 5, 111, 0, 0, 1358, 1359, + 5, 115, 0, 0, 1359, 260, 1, 0, 0, 0, 1360, 1361, 5, 111, 0, 0, 1361, 1362, 5, 110, 0, + 0, 1362, 1363, 5, 101, 0, 0, 1363, 1364, 5, 115, 0, 0, 1364, 262, 1, 0, 0, 0, 1365, + 1366, 5, 99, 0, 0, 1366, 1367, 5, 111, 0, 0, 1367, 1368, 5, 108, 0, 0, 1368, 1369, + 5, 115, 0, 0, 1369, 264, 1, 0, 0, 0, 1370, 1371, 5, 114, 0, 0, 1371, 1372, 5, 111, 0, + 0, 1372, 1373, 5, 119, 0, 0, 1373, 1374, 5, 115, 0, 0, 1374, 266, 1, 0, 0, 0, 1375, + 1376, 5, 100, 0, 0, 1376, 1377, 5, 105, 0, 0, 1377, 1378, 5, 97, 0, 0, 1378, 1379, + 5, 103, 0, 0, 1379, 268, 1, 0, 0, 0, 1380, 1381, 5, 110, 0, 0, 1381, 1382, 5, 111, 0, + 0, 1382, 1383, 5, 114, 0, 0, 1383, 1384, 5, 109, 0, 0, 1384, 270, 1, 0, 0, 0, 1385, + 1386, 5, 114, 0, 0, 1386, 1387, 5, 97, 0, 0, 1387, 1388, 5, 110, 0, 0, 1388, 1389, + 5, 107, 0, 0, 1389, 272, 1, 0, 0, 0, 1390, 1391, 5, 116, 0, 0, 1391, 1392, 5, 114, 0, + 0, 1392, 1393, 5, 97, 0, 0, 1393, 1394, 5, 99, 0, 0, 1394, 1398, 5, 101, 0, 0, 1395, + 1396, 5, 116, 0, 0, 1396, 1398, 5, 114, 0, 0, 1397, 1390, 1, 0, 0, 0, 1397, 1395, 1, + 0, 0, 0, 1398, 274, 1, 0, 0, 0, 1399, 1400, 5, 114, 0, 0, 1400, 1401, 5, 114, 0, 0, 1401, + 1402, 5, 101, 0, 0, 1402, 1403, 5, 102, 0, 0, 1403, 276, 1, 0, 0, 0, 1404, 1405, 5, + 104, 0, 0, 1405, 1406, 5, 115, 0, 0, 1406, 1407, 5, 116, 0, 0, 1407, 1408, 5, 97, 0, + 0, 1408, 1409, 5, 99, 0, 0, 1409, 1410, 5, 107, 0, 0, 1410, 278, 1, 0, 0, 0, 1411, 1412, + 5, 118, 0, 0, 1412, 1413, 5, 115, 0, 0, 1413, 1414, 5, 116, 0, 0, 1414, 1415, 5, 97, + 0, 0, 1415, 1416, 5, 99, 0, 0, 1416, 1417, 5, 107, 0, 0, 1417, 280, 1, 0, 0, 0, 1418, + 1419, 5, 111, 0, 0, 1419, 1420, 5, 114, 0, 0, 1420, 1421, 5, 116, 0, 0, 1421, 1451, + 5, 104, 0, 0, 1422, 1423, 5, 111, 0, 0, 1423, 1424, 5, 114, 0, 0, 1424, 1425, 5, 116, + 0, 0, 1425, 1426, 5, 104, 0, 0, 1426, 1451, 5, 111, 0, 0, 1427, 1428, 5, 111, 0, 0, + 1428, 1429, 5, 114, 0, 0, 1429, 1430, 5, 116, 0, 0, 1430, 1431, 5, 104, 0, 0, 1431, + 1432, 5, 111, 0, 0, 1432, 1433, 5, 103, 0, 0, 1433, 1434, 5, 111, 0, 0, 1434, 1435, + 5, 110, 0, 0, 1435, 1436, 5, 97, 0, 0, 1436, 1451, 5, 108, 0, 0, 1437, 1438, 5, 111, + 0, 0, 1438, 1439, 5, 114, 0, 0, 1439, 1440, 5, 116, 0, 0, 1440, 1441, 5, 104, 0, 0, + 1441, 1442, 5, 111, 0, 0, 1442, 1443, 5, 103, 0, 0, 1443, 1444, 5, 111, 0, 0, 1444, + 1445, 5, 110, 0, 0, 1445, 1446, 5, 97, 0, 0, 1446, 1447, 5, 108, 0, 0, 1447, 1448, + 5, 105, 0, 0, 1448, 1449, 5, 122, 0, 0, 1449, 1451, 5, 101, 0, 0, 1450, 1418, 1, 0, + 0, 0, 1450, 1422, 1, 0, 0, 0, 1450, 1427, 1, 0, 0, 0, 1450, 1437, 1, 0, 0, 0, 1451, 282, + 1, 0, 0, 0, 1452, 1453, 5, 110, 0, 0, 1453, 1454, 5, 117, 0, 0, 1454, 1455, 5, 108, + 0, 0, 1455, 1456, 5, 108, 0, 0, 1456, 1457, 5, 115, 0, 0, 1457, 1458, 5, 112, 0, 0, + 1458, 1459, 5, 97, 0, 0, 1459, 1460, 5, 99, 0, 0, 1460, 1461, 5, 101, 0, 0, 1461, 284, + 1, 0, 0, 0, 1462, 1463, 5, 101, 0, 0, 1463, 1464, 5, 105, 0, 0, 1464, 1482, 5, 103, + 0, 0, 1465, 1466, 5, 101, 0, 0, 1466, 1467, 5, 105, 0, 0, 1467, 1468, 5, 103, 0, 0, + 1468, 1469, 5, 101, 0, 0, 1469, 1482, 5, 110, 0, 0, 1470, 1471, 5, 100, 0, 0, 1471, + 1472, 5, 105, 0, 0, 1472, 1473, 5, 97, 0, 0, 1473, 1474, 5, 103, 0, 0, 1474, 1475, + 5, 111, 0, 0, 1475, 1476, 5, 110, 0, 0, 1476, 1477, 5, 97, 0, 0, 1477, 1478, 5, 108, + 0, 0, 1478, 1479, 5, 105, 0, 0, 1479, 1480, 5, 122, 0, 0, 1480, 1482, 5, 101, 0, 0, + 1481, 1462, 1, 0, 0, 0, 1481, 1465, 1, 0, 0, 0, 1481, 1470, 1, 0, 0, 0, 1482, 286, 1, + 0, 0, 0, 1483, 1484, 5, 101, 0, 0, 1484, 1485, 5, 105, 0, 0, 1485, 1486, 5, 103, 0, + 0, 1486, 1487, 5, 101, 0, 0, 1487, 1488, 5, 110, 0, 0, 1488, 1489, 5, 118, 0, 0, 1489, + 1490, 5, 97, 0, 0, 1490, 1491, 5, 108, 0, 0, 1491, 1504, 5, 115, 0, 0, 1492, 1493, + 5, 101, 0, 0, 1493, 1494, 5, 105, 0, 0, 1494, 1495, 5, 103, 0, 0, 1495, 1496, 5, 101, + 0, 0, 1496, 1497, 5, 110, 0, 0, 1497, 1498, 5, 118, 0, 0, 1498, 1499, 5, 97, 0, 0, 1499, + 1500, 5, 108, 0, 0, 1500, 1501, 5, 117, 0, 0, 1501, 1502, 5, 101, 0, 0, 1502, 1504, + 5, 115, 0, 0, 1503, 1483, 1, 0, 0, 0, 1503, 1492, 1, 0, 0, 0, 1504, 288, 1, 0, 0, 0, 1505, + 1506, 5, 101, 0, 0, 1506, 1507, 5, 105, 0, 0, 1507, 1508, 5, 103, 0, 0, 1508, 1509, + 5, 101, 0, 0, 1509, 1510, 5, 110, 0, 0, 1510, 1511, 5, 118, 0, 0, 1511, 1512, 5, 101, + 0, 0, 1512, 1513, 5, 99, 0, 0, 1513, 1514, 5, 116, 0, 0, 1514, 1528, 5, 115, 0, 0, 1515, + 1516, 5, 101, 0, 0, 1516, 1517, 5, 105, 0, 0, 1517, 1518, 5, 103, 0, 0, 1518, 1519, + 5, 101, 0, 0, 1519, 1520, 5, 110, 0, 0, 1520, 1521, 5, 118, 0, 0, 1521, 1522, 5, 101, + 0, 0, 1522, 1523, 5, 99, 0, 0, 1523, 1524, 5, 116, 0, 0, 1524, 1525, 5, 111, 0, 0, 1525, + 1526, 5, 114, 0, 0, 1526, 1528, 5, 115, 0, 0, 1527, 1505, 1, 0, 0, 0, 1527, 1515, 1, + 0, 0, 0, 1528, 290, 1, 0, 0, 0, 1529, 1530, 5, 115, 0, 0, 1530, 1531, 5, 118, 0, 0, 1531, + 1536, 5, 100, 0, 0, 1532, 1533, 5, 83, 0, 0, 1533, 1534, 5, 86, 0, 0, 1534, 1536, 5, + 68, 0, 0, 1535, 1529, 1, 0, 0, 0, 1535, 1532, 1, 0, 0, 0, 1536, 292, 1, 0, 0, 0, 1537, + 1538, 5, 92, 0, 0, 1538, 1539, 5, 116, 0, 0, 1539, 1540, 5, 105, 0, 0, 1540, 1541, + 5, 109, 0, 0, 1541, 1542, 5, 101, 0, 0, 1542, 1543, 5, 115, 0, 0, 1543, 294, 1, 0, 0, + 0, 1544, 1545, 5, 92, 0, 0, 1545, 1546, 5, 99, 0, 0, 1546, 1547, 5, 100, 0, 0, 1547, + 1548, 5, 111, 0, 0, 1548, 1549, 5, 116, 0, 0, 1549, 296, 1, 0, 0, 0, 1550, 1551, 5, + 92, 0, 0, 1551, 1552, 5, 100, 0, 0, 1552, 1553, 5, 105, 0, 0, 1553, 1554, 5, 118, 0, + 0, 1554, 298, 1, 0, 0, 0, 1555, 1556, 5, 92, 0, 0, 1556, 1557, 5, 102, 0, 0, 1557, 1558, + 5, 114, 0, 0, 1558, 1559, 5, 97, 0, 0, 1559, 1560, 5, 99, 0, 0, 1560, 300, 1, 0, 0, 0, + 1561, 1562, 5, 92, 0, 0, 1562, 1563, 5, 98, 0, 0, 1563, 1564, 5, 105, 0, 0, 1564, 1565, + 5, 110, 0, 0, 1565, 1566, 5, 111, 0, 0, 1566, 1582, 5, 109, 0, 0, 1567, 1568, 5, 92, + 0, 0, 1568, 1569, 5, 116, 0, 0, 1569, 1570, 5, 98, 0, 0, 1570, 1571, 5, 105, 0, 0, 1571, + 1572, 5, 110, 0, 0, 1572, 1573, 5, 111, 0, 0, 1573, 1582, 5, 109, 0, 0, 1574, 1575, + 5, 92, 0, 0, 1575, 1576, 5, 100, 0, 0, 1576, 1577, 5, 98, 0, 0, 1577, 1578, 5, 105, + 0, 0, 1578, 1579, 5, 110, 0, 0, 1579, 1580, 5, 111, 0, 0, 1580, 1582, 5, 109, 0, 0, + 1581, 1561, 1, 0, 0, 0, 1581, 1567, 1, 0, 0, 0, 1581, 1574, 1, 0, 0, 0, 1582, 302, 1, + 0, 0, 0, 1583, 1584, 5, 92, 0, 0, 1584, 1585, 5, 99, 0, 0, 1585, 1586, 5, 104, 0, 0, + 1586, 1587, 5, 111, 0, 0, 1587, 1588, 5, 111, 0, 0, 1588, 1589, 5, 115, 0, 0, 1589, + 1590, 5, 101, 0, 0, 1590, 304, 1, 0, 0, 0, 1591, 1592, 5, 92, 0, 0, 1592, 1593, 5, 109, + 0, 0, 1593, 1594, 5, 111, 0, 0, 1594, 1595, 5, 100, 0, 0, 1595, 306, 1, 0, 0, 0, 1596, + 1597, 5, 92, 0, 0, 1597, 1598, 5, 109, 0, 0, 1598, 1599, 5, 97, 0, 0, 1599, 1600, 5, + 116, 0, 0, 1600, 1601, 5, 104, 0, 0, 1601, 1602, 5, 105, 0, 0, 1602, 1603, 5, 116, + 0, 0, 1603, 308, 1, 0, 0, 0, 1604, 1605, 5, 92, 0, 0, 1605, 1606, 5, 111, 0, 0, 1606, + 1607, 5, 112, 0, 0, 1607, 1608, 5, 101, 0, 0, 1608, 1609, 5, 114, 0, 0, 1609, 1610, + 5, 97, 0, 0, 1610, 1611, 5, 116, 0, 0, 1611, 1612, 5, 111, 0, 0, 1612, 1613, 5, 114, + 0, 0, 1613, 1614, 5, 110, 0, 0, 1614, 1615, 5, 97, 0, 0, 1615, 1616, 5, 109, 0, 0, 1616, + 1617, 5, 101, 0, 0, 1617, 310, 1, 0, 0, 0, 1618, 1619, 5, 109, 0, 0, 1619, 1620, 5, + 97, 0, 0, 1620, 1621, 5, 116, 0, 0, 1621, 1622, 5, 114, 0, 0, 1622, 1623, 5, 105, 0, + 0, 1623, 1624, 5, 120, 0, 0, 1624, 312, 1, 0, 0, 0, 1625, 1626, 5, 112, 0, 0, 1626, + 1627, 5, 109, 0, 0, 1627, 1628, 5, 97, 0, 0, 1628, 1629, 5, 116, 0, 0, 1629, 1630, + 5, 114, 0, 0, 1630, 1631, 5, 105, 0, 0, 1631, 1632, 5, 120, 0, 0, 1632, 314, 1, 0, 0, + 0, 1633, 1634, 5, 98, 0, 0, 1634, 1635, 5, 109, 0, 0, 1635, 1636, 5, 97, 0, 0, 1636, + 1637, 5, 116, 0, 0, 1637, 1638, 5, 114, 0, 0, 1638, 1639, 5, 105, 0, 0, 1639, 1640, + 5, 120, 0, 0, 1640, 316, 1, 0, 0, 0, 1641, 1642, 5, 118, 0, 0, 1642, 1643, 5, 109, 0, + 0, 1643, 1644, 5, 97, 0, 0, 1644, 1645, 5, 116, 0, 0, 1645, 1646, 5, 114, 0, 0, 1646, + 1647, 5, 105, 0, 0, 1647, 1648, 5, 120, 0, 0, 1648, 318, 1, 0, 0, 0, 1649, 1653, 3, + 311, 155, 0, 1650, 1653, 3, 313, 156, 0, 1651, 1653, 3, 315, 157, 0, 1652, 1649, + 1, 0, 0, 0, 1652, 1650, 1, 0, 0, 0, 1652, 1651, 1, 0, 0, 0, 1653, 320, 1, 0, 0, 0, 1654, + 1655, 5, 92, 0, 0, 1655, 1656, 5, 98, 0, 0, 1656, 1657, 5, 101, 0, 0, 1657, 1658, 5, + 103, 0, 0, 1658, 1659, 5, 105, 0, 0, 1659, 1660, 5, 110, 0, 0, 1660, 1661, 1, 0, 0, + 0, 1661, 1662, 3, 109, 54, 0, 1662, 1663, 3, 319, 159, 0, 1663, 1664, 3, 111, 55, + 0, 1664, 322, 1, 0, 0, 0, 1665, 1666, 5, 92, 0, 0, 1666, 1667, 5, 101, 0, 0, 1667, 1668, + 5, 110, 0, 0, 1668, 1669, 5, 100, 0, 0, 1669, 1670, 1, 0, 0, 0, 1670, 1671, 3, 109, + 54, 0, 1671, 1672, 3, 319, 159, 0, 1672, 1673, 3, 111, 55, 0, 1673, 324, 1, 0, 0, 0, + 1674, 1675, 5, 92, 0, 0, 1675, 1676, 5, 98, 0, 0, 1676, 1677, 5, 101, 0, 0, 1677, 1678, + 5, 103, 0, 0, 1678, 1679, 5, 105, 0, 0, 1679, 1680, 5, 110, 0, 0, 1680, 1681, 1, 0, + 0, 0, 1681, 1682, 3, 109, 54, 0, 1682, 1683, 3, 317, 158, 0, 1683, 1684, 3, 111, 55, + 0, 1684, 326, 1, 0, 0, 0, 1685, 1686, 5, 92, 0, 0, 1686, 1687, 5, 101, 0, 0, 1687, 1688, + 5, 110, 0, 0, 1688, 1689, 5, 100, 0, 0, 1689, 1690, 1, 0, 0, 0, 1690, 1691, 3, 109, + 54, 0, 1691, 1692, 3, 317, 158, 0, 1692, 1693, 3, 111, 55, 0, 1693, 328, 1, 0, 0, 0, + 1694, 1695, 5, 38, 0, 0, 1695, 330, 1, 0, 0, 0, 1696, 1697, 5, 92, 0, 0, 1697, 1698, + 5, 92, 0, 0, 1698, 332, 1, 0, 0, 0, 1699, 1700, 5, 95, 0, 0, 1700, 334, 1, 0, 0, 0, 1701, + 1702, 5, 94, 0, 0, 1702, 336, 1, 0, 0, 0, 1703, 1704, 5, 58, 0, 0, 1704, 338, 1, 0, 0, + 0, 1705, 1706, 5, 59, 0, 0, 1706, 340, 1, 0, 0, 0, 1707, 1708, 5, 44, 0, 0, 1708, 342, + 1, 0, 0, 0, 1709, 1710, 5, 46, 0, 0, 1710, 344, 1, 0, 0, 0, 1711, 1712, 7, 0, 0, 0, 1712, + 346, 1, 0, 0, 0, 1713, 1717, 5, 100, 0, 0, 1714, 1716, 3, 345, 172, 0, 1715, 1714, + 1, 0, 0, 0, 1716, 1719, 1, 0, 0, 0, 1717, 1718, 1, 0, 0, 0, 1717, 1715, 1, 0, 0, 0, 1718, + 1727, 1, 0, 0, 0, 1719, 1717, 1, 0, 0, 0, 1720, 1728, 7, 1, 0, 0, 1721, 1723, 5, 92, + 0, 0, 1722, 1724, 7, 1, 0, 0, 1723, 1722, 1, 0, 0, 0, 1724, 1725, 1, 0, 0, 0, 1725, 1723, + 1, 0, 0, 0, 1725, 1726, 1, 0, 0, 0, 1726, 1728, 1, 0, 0, 0, 1727, 1720, 1, 0, 0, 0, 1727, + 1721, 1, 0, 0, 0, 1728, 348, 1, 0, 0, 0, 1729, 1744, 5, 101, 0, 0, 1730, 1731, 5, 92, + 0, 0, 1731, 1732, 5, 101, 0, 0, 1732, 1733, 5, 120, 0, 0, 1733, 1734, 5, 112, 0, 0, + 1734, 1735, 5, 111, 0, 0, 1735, 1736, 5, 110, 0, 0, 1736, 1737, 5, 101, 0, 0, 1737, + 1738, 5, 110, 0, 0, 1738, 1739, 5, 116, 0, 0, 1739, 1740, 5, 105, 0, 0, 1740, 1741, + 5, 97, 0, 0, 1741, 1742, 5, 108, 0, 0, 1742, 1744, 5, 69, 0, 0, 1743, 1729, 1, 0, 0, + 0, 1743, 1730, 1, 0, 0, 0, 1744, 350, 1, 0, 0, 0, 1745, 1746, 5, 69, 0, 0, 1746, 352, + 1, 0, 0, 0, 1747, 1748, 7, 2, 0, 0, 1748, 354, 1, 0, 0, 0, 1749, 1750, 7, 1, 0, 0, 1750, + 356, 1, 0, 0, 0, 1751, 1752, 7, 3, 0, 0, 1752, 358, 1, 0, 0, 0, 1753, 1754, 5, 92, 0, + 0, 1754, 1755, 5, 120, 0, 0, 1755, 1756, 5, 114, 0, 0, 1756, 1757, 5, 105, 0, 0, 1757, + 1758, 5, 103, 0, 0, 1758, 1759, 5, 104, 0, 0, 1759, 1760, 5, 116, 0, 0, 1760, 1761, + 5, 97, 0, 0, 1761, 1762, 5, 114, 0, 0, 1762, 1763, 5, 114, 0, 0, 1763, 1764, 5, 111, + 0, 0, 1764, 1778, 5, 119, 0, 0, 1765, 1766, 5, 92, 0, 0, 1766, 1767, 5, 120, 0, 0, 1767, + 1768, 5, 82, 0, 0, 1768, 1769, 5, 105, 0, 0, 1769, 1770, 5, 103, 0, 0, 1770, 1771, + 5, 104, 0, 0, 1771, 1772, 5, 116, 0, 0, 1772, 1773, 5, 97, 0, 0, 1773, 1774, 5, 114, + 0, 0, 1774, 1775, 5, 114, 0, 0, 1775, 1776, 5, 111, 0, 0, 1776, 1778, 5, 119, 0, 0, + 1777, 1753, 1, 0, 0, 0, 1777, 1765, 1, 0, 0, 0, 1778, 360, 1, 0, 0, 0, 1779, 1780, 5, + 60, 0, 0, 1780, 1781, 5, 45, 0, 0, 1781, 1816, 5, 62, 0, 0, 1782, 1783, 5, 60, 0, 0, + 1783, 1784, 5, 61, 0, 0, 1784, 1816, 5, 62, 0, 0, 1785, 1786, 5, 92, 0, 0, 1786, 1787, + 5, 108, 0, 0, 1787, 1788, 5, 101, 0, 0, 1788, 1789, 5, 102, 0, 0, 1789, 1790, 5, 116, + 0, 0, 1790, 1791, 5, 114, 0, 0, 1791, 1792, 5, 105, 0, 0, 1792, 1793, 5, 103, 0, 0, + 1793, 1794, 5, 104, 0, 0, 1794, 1795, 5, 116, 0, 0, 1795, 1796, 5, 97, 0, 0, 1796, + 1797, 5, 114, 0, 0, 1797, 1798, 5, 114, 0, 0, 1798, 1799, 5, 111, 0, 0, 1799, 1816, + 5, 119, 0, 0, 1800, 1801, 5, 92, 0, 0, 1801, 1802, 5, 76, 0, 0, 1802, 1803, 5, 101, + 0, 0, 1803, 1804, 5, 102, 0, 0, 1804, 1805, 5, 116, 0, 0, 1805, 1806, 5, 114, 0, 0, + 1806, 1807, 5, 105, 0, 0, 1807, 1808, 5, 103, 0, 0, 1808, 1809, 5, 104, 0, 0, 1809, + 1810, 5, 116, 0, 0, 1810, 1811, 5, 97, 0, 0, 1811, 1812, 5, 114, 0, 0, 1812, 1813, + 5, 114, 0, 0, 1813, 1814, 5, 111, 0, 0, 1814, 1816, 5, 119, 0, 0, 1815, 1779, 1, 0, + 0, 0, 1815, 1782, 1, 0, 0, 0, 1815, 1785, 1, 0, 0, 0, 1815, 1800, 1, 0, 0, 0, 1816, 362, + 1, 0, 0, 0, 1817, 1819, 3, 357, 178, 0, 1818, 1817, 1, 0, 0, 0, 1819, 1820, 1, 0, 0, + 0, 1820, 1818, 1, 0, 0, 0, 1820, 1821, 1, 0, 0, 0, 1821, 1829, 1, 0, 0, 0, 1822, 1823, + 3, 341, 170, 0, 1823, 1824, 3, 357, 178, 0, 1824, 1825, 3, 357, 178, 0, 1825, 1826, + 3, 357, 178, 0, 1826, 1828, 1, 0, 0, 0, 1827, 1822, 1, 0, 0, 0, 1828, 1831, 1, 0, 0, + 0, 1829, 1827, 1, 0, 0, 0, 1829, 1830, 1, 0, 0, 0, 1830, 1855, 1, 0, 0, 0, 1831, 1829, + 1, 0, 0, 0, 1832, 1834, 3, 357, 178, 0, 1833, 1832, 1, 0, 0, 0, 1834, 1837, 1, 0, 0, + 0, 1835, 1833, 1, 0, 0, 0, 1835, 1836, 1, 0, 0, 0, 1836, 1845, 1, 0, 0, 0, 1837, 1835, + 1, 0, 0, 0, 1838, 1839, 3, 341, 170, 0, 1839, 1840, 3, 357, 178, 0, 1840, 1841, 3, + 357, 178, 0, 1841, 1842, 3, 357, 178, 0, 1842, 1844, 1, 0, 0, 0, 1843, 1838, 1, 0, + 0, 0, 1844, 1847, 1, 0, 0, 0, 1845, 1843, 1, 0, 0, 0, 1845, 1846, 1, 0, 0, 0, 1846, 1848, + 1, 0, 0, 0, 1847, 1845, 1, 0, 0, 0, 1848, 1850, 3, 343, 171, 0, 1849, 1851, 3, 357, + 178, 0, 1850, 1849, 1, 0, 0, 0, 1851, 1852, 1, 0, 0, 0, 1852, 1850, 1, 0, 0, 0, 1852, + 1853, 1, 0, 0, 0, 1853, 1855, 1, 0, 0, 0, 1854, 1818, 1, 0, 0, 0, 1854, 1835, 1, 0, 0, + 0, 1855, 364, 1, 0, 0, 0, 1856, 1857, 3, 363, 181, 0, 1857, 1860, 3, 351, 175, 0, 1858, + 1861, 3, 95, 47, 0, 1859, 1861, 3, 93, 46, 0, 1860, 1858, 1, 0, 0, 0, 1860, 1859, 1, + 0, 0, 0, 1860, 1861, 1, 0, 0, 0, 1861, 1863, 1, 0, 0, 0, 1862, 1864, 3, 357, 178, 0, + 1863, 1862, 1, 0, 0, 0, 1864, 1865, 1, 0, 0, 0, 1865, 1863, 1, 0, 0, 0, 1865, 1866, + 1, 0, 0, 0, 1866, 366, 1, 0, 0, 0, 1867, 1868, 5, 92, 0, 0, 1868, 1869, 5, 105, 0, 0, + 1869, 1870, 5, 110, 0, 0, 1870, 368, 1, 0, 0, 0, 1871, 1872, 5, 61, 0, 0, 1872, 370, + 1, 0, 0, 0, 1873, 1874, 5, 61, 0, 0, 1874, 1882, 5, 61, 0, 0, 1875, 1876, 5, 92, 0, 0, + 1876, 1877, 5, 101, 0, 0, 1877, 1878, 5, 113, 0, 0, 1878, 1879, 5, 117, 0, 0, 1879, + 1880, 5, 105, 0, 0, 1880, 1882, 5, 118, 0, 0, 1881, 1873, 1, 0, 0, 0, 1881, 1875, 1, + 0, 0, 0, 1882, 372, 1, 0, 0, 0, 1883, 1884, 5, 60, 0, 0, 1884, 374, 1, 0, 0, 0, 1885, + 1886, 5, 92, 0, 0, 1886, 1887, 5, 108, 0, 0, 1887, 1888, 5, 101, 0, 0, 1888, 1902, + 5, 113, 0, 0, 1889, 1890, 5, 92, 0, 0, 1890, 1891, 5, 108, 0, 0, 1891, 1902, 5, 101, + 0, 0, 1892, 1893, 5, 92, 0, 0, 1893, 1894, 5, 108, 0, 0, 1894, 1895, 5, 101, 0, 0, 1895, + 1896, 5, 113, 0, 0, 1896, 1897, 5, 115, 0, 0, 1897, 1898, 5, 108, 0, 0, 1898, 1899, + 5, 97, 0, 0, 1899, 1900, 5, 110, 0, 0, 1900, 1902, 5, 116, 0, 0, 1901, 1885, 1, 0, 0, + 0, 1901, 1889, 1, 0, 0, 0, 1901, 1892, 1, 0, 0, 0, 1902, 376, 1, 0, 0, 0, 1903, 1904, + 5, 62, 0, 0, 1904, 378, 1, 0, 0, 0, 1905, 1906, 5, 92, 0, 0, 1906, 1907, 5, 103, 0, 0, + 1907, 1908, 5, 101, 0, 0, 1908, 1922, 5, 113, 0, 0, 1909, 1910, 5, 92, 0, 0, 1910, + 1911, 5, 103, 0, 0, 1911, 1922, 5, 101, 0, 0, 1912, 1913, 5, 92, 0, 0, 1913, 1914, + 5, 103, 0, 0, 1914, 1915, 5, 101, 0, 0, 1915, 1916, 5, 113, 0, 0, 1916, 1917, 5, 115, + 0, 0, 1917, 1918, 5, 108, 0, 0, 1918, 1919, 5, 97, 0, 0, 1919, 1920, 5, 110, 0, 0, 1920, + 1922, 5, 116, 0, 0, 1921, 1905, 1, 0, 0, 0, 1921, 1909, 1, 0, 0, 0, 1921, 1912, 1, 0, + 0, 0, 1922, 380, 1, 0, 0, 0, 1923, 1924, 5, 33, 0, 0, 1924, 1946, 5, 61, 0, 0, 1925, + 1926, 5, 33, 0, 0, 1926, 1927, 5, 61, 0, 0, 1927, 1946, 5, 61, 0, 0, 1928, 1929, 5, + 92, 0, 0, 1929, 1930, 5, 110, 0, 0, 1930, 1946, 5, 101, 0, 0, 1931, 1932, 5, 92, 0, + 0, 1932, 1933, 5, 110, 0, 0, 1933, 1934, 5, 101, 0, 0, 1934, 1946, 5, 113, 0, 0, 1935, + 1936, 5, 92, 0, 0, 1936, 1937, 5, 110, 0, 0, 1937, 1938, 5, 111, 0, 0, 1938, 1939, + 5, 116, 0, 0, 1939, 1940, 5, 92, 0, 0, 1940, 1941, 5, 101, 0, 0, 1941, 1942, 5, 113, + 0, 0, 1942, 1943, 5, 117, 0, 0, 1943, 1944, 5, 105, 0, 0, 1944, 1946, 5, 118, 0, 0, + 1945, 1923, 1, 0, 0, 0, 1945, 1925, 1, 0, 0, 0, 1945, 1928, 1, 0, 0, 0, 1945, 1931, + 1, 0, 0, 0, 1945, 1935, 1, 0, 0, 0, 1946, 382, 1, 0, 0, 0, 1947, 1948, 5, 33, 0, 0, 1948, + 384, 1, 0, 0, 0, 1949, 1950, 5, 92, 0, 0, 1950, 1951, 5, 37, 0, 0, 1951, 386, 1, 0, 0, + 0, 1952, 1953, 3, 363, 181, 0, 1953, 1954, 3, 385, 192, 0, 1954, 388, 1, 0, 0, 0, 1955, + 1956, 5, 92, 0, 0, 1956, 1957, 5, 99, 0, 0, 1957, 1958, 5, 104, 0, 0, 1958, 1959, 5, + 97, 0, 0, 1959, 1960, 5, 114, 0, 0, 1960, 1961, 5, 34, 0, 0, 1961, 1962, 5, 48, 0, 0, + 1962, 1963, 5, 48, 0, 0, 1963, 1964, 5, 48, 0, 0, 1964, 1965, 5, 51, 0, 0, 1965, 1966, + 5, 57, 0, 0, 1966, 2341, 5, 49, 0, 0, 1967, 1968, 5, 92, 0, 0, 1968, 1969, 5, 97, 0, + 0, 1969, 1970, 5, 108, 0, 0, 1970, 1971, 5, 112, 0, 0, 1971, 1972, 5, 104, 0, 0, 1972, + 2341, 5, 97, 0, 0, 1973, 1974, 5, 92, 0, 0, 1974, 1975, 5, 99, 0, 0, 1975, 1976, 5, + 104, 0, 0, 1976, 1977, 5, 97, 0, 0, 1977, 1978, 5, 114, 0, 0, 1978, 1979, 5, 34, 0, + 0, 1979, 1980, 5, 48, 0, 0, 1980, 1981, 5, 48, 0, 0, 1981, 1982, 5, 48, 0, 0, 1982, + 1983, 5, 51, 0, 0, 1983, 1984, 5, 57, 0, 0, 1984, 2341, 5, 50, 0, 0, 1985, 1986, 5, + 92, 0, 0, 1986, 1987, 5, 98, 0, 0, 1987, 1988, 5, 101, 0, 0, 1988, 1989, 5, 116, 0, + 0, 1989, 2341, 5, 97, 0, 0, 1990, 1991, 5, 92, 0, 0, 1991, 1992, 5, 71, 0, 0, 1992, + 1993, 5, 97, 0, 0, 1993, 1994, 5, 109, 0, 0, 1994, 1995, 5, 109, 0, 0, 1995, 2341, + 5, 97, 0, 0, 1996, 1997, 5, 92, 0, 0, 1997, 1998, 5, 103, 0, 0, 1998, 1999, 5, 97, 0, + 0, 1999, 2000, 5, 109, 0, 0, 2000, 2001, 5, 109, 0, 0, 2001, 2341, 5, 97, 0, 0, 2002, + 2003, 5, 92, 0, 0, 2003, 2004, 5, 68, 0, 0, 2004, 2005, 5, 101, 0, 0, 2005, 2006, 5, + 108, 0, 0, 2006, 2007, 5, 116, 0, 0, 2007, 2341, 5, 97, 0, 0, 2008, 2009, 5, 92, 0, + 0, 2009, 2010, 5, 100, 0, 0, 2010, 2011, 5, 101, 0, 0, 2011, 2012, 5, 108, 0, 0, 2012, + 2013, 5, 116, 0, 0, 2013, 2341, 5, 97, 0, 0, 2014, 2015, 5, 92, 0, 0, 2015, 2016, 5, + 99, 0, 0, 2016, 2017, 5, 104, 0, 0, 2017, 2018, 5, 97, 0, 0, 2018, 2019, 5, 114, 0, + 0, 2019, 2020, 5, 34, 0, 0, 2020, 2021, 5, 48, 0, 0, 2021, 2022, 5, 48, 0, 0, 2022, + 2023, 5, 48, 0, 0, 2023, 2024, 5, 49, 0, 0, 2024, 2025, 5, 57, 0, 0, 2025, 2341, 5, + 48, 0, 0, 2026, 2027, 5, 92, 0, 0, 2027, 2028, 5, 101, 0, 0, 2028, 2029, 5, 112, 0, + 0, 2029, 2030, 5, 115, 0, 0, 2030, 2031, 5, 105, 0, 0, 2031, 2032, 5, 108, 0, 0, 2032, + 2033, 5, 111, 0, 0, 2033, 2341, 5, 110, 0, 0, 2034, 2035, 5, 92, 0, 0, 2035, 2036, + 5, 118, 0, 0, 2036, 2037, 5, 97, 0, 0, 2037, 2038, 5, 114, 0, 0, 2038, 2039, 5, 101, + 0, 0, 2039, 2040, 5, 112, 0, 0, 2040, 2041, 5, 115, 0, 0, 2041, 2042, 5, 105, 0, 0, + 2042, 2043, 5, 108, 0, 0, 2043, 2044, 5, 111, 0, 0, 2044, 2341, 5, 110, 0, 0, 2045, + 2046, 5, 92, 0, 0, 2046, 2047, 5, 99, 0, 0, 2047, 2048, 5, 104, 0, 0, 2048, 2049, 5, + 97, 0, 0, 2049, 2050, 5, 114, 0, 0, 2050, 2051, 5, 34, 0, 0, 2051, 2052, 5, 48, 0, 0, + 2052, 2053, 5, 48, 0, 0, 2053, 2054, 5, 48, 0, 0, 2054, 2055, 5, 51, 0, 0, 2055, 2056, + 5, 57, 0, 0, 2056, 2341, 5, 54, 0, 0, 2057, 2058, 5, 92, 0, 0, 2058, 2059, 5, 122, 0, + 0, 2059, 2060, 5, 101, 0, 0, 2060, 2061, 5, 116, 0, 0, 2061, 2341, 5, 97, 0, 0, 2062, + 2063, 5, 92, 0, 0, 2063, 2064, 5, 99, 0, 0, 2064, 2065, 5, 104, 0, 0, 2065, 2066, 5, + 97, 0, 0, 2066, 2067, 5, 114, 0, 0, 2067, 2068, 5, 34, 0, 0, 2068, 2069, 5, 48, 0, 0, + 2069, 2070, 5, 48, 0, 0, 2070, 2071, 5, 48, 0, 0, 2071, 2072, 5, 51, 0, 0, 2072, 2073, + 5, 57, 0, 0, 2073, 2341, 5, 55, 0, 0, 2074, 2075, 5, 92, 0, 0, 2075, 2076, 5, 101, 0, + 0, 2076, 2077, 5, 116, 0, 0, 2077, 2341, 5, 97, 0, 0, 2078, 2079, 5, 92, 0, 0, 2079, + 2080, 5, 84, 0, 0, 2080, 2081, 5, 104, 0, 0, 2081, 2082, 5, 101, 0, 0, 2082, 2083, + 5, 116, 0, 0, 2083, 2341, 5, 97, 0, 0, 2084, 2085, 5, 92, 0, 0, 2085, 2086, 5, 116, + 0, 0, 2086, 2087, 5, 104, 0, 0, 2087, 2088, 5, 101, 0, 0, 2088, 2089, 5, 116, 0, 0, + 2089, 2341, 5, 97, 0, 0, 2090, 2091, 5, 92, 0, 0, 2091, 2092, 5, 118, 0, 0, 2092, 2093, + 5, 97, 0, 0, 2093, 2094, 5, 114, 0, 0, 2094, 2095, 5, 116, 0, 0, 2095, 2096, 5, 104, + 0, 0, 2096, 2097, 5, 101, 0, 0, 2097, 2098, 5, 116, 0, 0, 2098, 2341, 5, 97, 0, 0, 2099, + 2100, 5, 92, 0, 0, 2100, 2101, 5, 99, 0, 0, 2101, 2102, 5, 104, 0, 0, 2102, 2103, 5, + 97, 0, 0, 2103, 2104, 5, 114, 0, 0, 2104, 2105, 5, 34, 0, 0, 2105, 2106, 5, 48, 0, 0, + 2106, 2107, 5, 48, 0, 0, 2107, 2108, 5, 48, 0, 0, 2108, 2109, 5, 51, 0, 0, 2109, 2110, + 5, 57, 0, 0, 2110, 2341, 5, 57, 0, 0, 2111, 2112, 5, 92, 0, 0, 2112, 2113, 5, 105, 0, + 0, 2113, 2114, 5, 111, 0, 0, 2114, 2115, 5, 116, 0, 0, 2115, 2341, 5, 97, 0, 0, 2116, + 2117, 5, 92, 0, 0, 2117, 2118, 5, 99, 0, 0, 2118, 2119, 5, 104, 0, 0, 2119, 2120, 5, + 97, 0, 0, 2120, 2121, 5, 114, 0, 0, 2121, 2122, 5, 34, 0, 0, 2122, 2123, 5, 48, 0, 0, + 2123, 2124, 5, 48, 0, 0, 2124, 2125, 5, 48, 0, 0, 2125, 2126, 5, 51, 0, 0, 2126, 2127, + 5, 57, 0, 0, 2127, 2341, 5, 65, 0, 0, 2128, 2129, 5, 92, 0, 0, 2129, 2130, 5, 107, 0, + 0, 2130, 2131, 5, 97, 0, 0, 2131, 2132, 5, 112, 0, 0, 2132, 2133, 5, 112, 0, 0, 2133, + 2341, 5, 97, 0, 0, 2134, 2135, 5, 92, 0, 0, 2135, 2136, 5, 76, 0, 0, 2136, 2137, 5, + 97, 0, 0, 2137, 2138, 5, 109, 0, 0, 2138, 2139, 5, 98, 0, 0, 2139, 2140, 5, 100, 0, + 0, 2140, 2341, 5, 97, 0, 0, 2141, 2142, 5, 92, 0, 0, 2142, 2143, 5, 108, 0, 0, 2143, + 2144, 5, 97, 0, 0, 2144, 2145, 5, 109, 0, 0, 2145, 2146, 5, 98, 0, 0, 2146, 2147, 5, + 100, 0, 0, 2147, 2341, 5, 97, 0, 0, 2148, 2149, 5, 92, 0, 0, 2149, 2150, 5, 99, 0, 0, + 2150, 2151, 5, 104, 0, 0, 2151, 2152, 5, 97, 0, 0, 2152, 2153, 5, 114, 0, 0, 2153, + 2154, 5, 34, 0, 0, 2154, 2155, 5, 48, 0, 0, 2155, 2156, 5, 48, 0, 0, 2156, 2157, 5, + 48, 0, 0, 2157, 2158, 5, 51, 0, 0, 2158, 2159, 5, 57, 0, 0, 2159, 2341, 5, 67, 0, 0, + 2160, 2161, 5, 92, 0, 0, 2161, 2162, 5, 109, 0, 0, 2162, 2341, 5, 117, 0, 0, 2163, + 2164, 5, 92, 0, 0, 2164, 2165, 5, 99, 0, 0, 2165, 2166, 5, 104, 0, 0, 2166, 2167, 5, + 97, 0, 0, 2167, 2168, 5, 114, 0, 0, 2168, 2169, 5, 34, 0, 0, 2169, 2170, 5, 48, 0, 0, + 2170, 2171, 5, 48, 0, 0, 2171, 2172, 5, 48, 0, 0, 2172, 2173, 5, 51, 0, 0, 2173, 2174, + 5, 57, 0, 0, 2174, 2341, 5, 68, 0, 0, 2175, 2176, 5, 92, 0, 0, 2176, 2177, 5, 110, 0, + 0, 2177, 2341, 5, 117, 0, 0, 2178, 2179, 5, 92, 0, 0, 2179, 2180, 5, 88, 0, 0, 2180, + 2341, 5, 105, 0, 0, 2181, 2182, 5, 92, 0, 0, 2182, 2183, 5, 120, 0, 0, 2183, 2341, + 5, 105, 0, 0, 2184, 2185, 5, 92, 0, 0, 2185, 2186, 5, 99, 0, 0, 2186, 2187, 5, 104, + 0, 0, 2187, 2188, 5, 97, 0, 0, 2188, 2189, 5, 114, 0, 0, 2189, 2190, 5, 34, 0, 0, 2190, + 2191, 5, 48, 0, 0, 2191, 2192, 5, 48, 0, 0, 2192, 2193, 5, 48, 0, 0, 2193, 2194, 5, + 51, 0, 0, 2194, 2195, 5, 57, 0, 0, 2195, 2341, 5, 70, 0, 0, 2196, 2197, 5, 92, 0, 0, + 2197, 2198, 5, 111, 0, 0, 2198, 2199, 5, 109, 0, 0, 2199, 2200, 5, 105, 0, 0, 2200, + 2201, 5, 99, 0, 0, 2201, 2202, 5, 114, 0, 0, 2202, 2203, 5, 111, 0, 0, 2203, 2341, + 5, 110, 0, 0, 2204, 2205, 5, 92, 0, 0, 2205, 2206, 5, 80, 0, 0, 2206, 2341, 5, 105, + 0, 0, 2207, 2208, 5, 92, 0, 0, 2208, 2209, 5, 118, 0, 0, 2209, 2210, 5, 97, 0, 0, 2210, + 2211, 5, 114, 0, 0, 2211, 2212, 5, 112, 0, 0, 2212, 2341, 5, 105, 0, 0, 2213, 2214, + 5, 92, 0, 0, 2214, 2215, 5, 99, 0, 0, 2215, 2216, 5, 104, 0, 0, 2216, 2217, 5, 97, 0, + 0, 2217, 2218, 5, 114, 0, 0, 2218, 2219, 5, 34, 0, 0, 2219, 2220, 5, 48, 0, 0, 2220, + 2221, 5, 48, 0, 0, 2221, 2222, 5, 48, 0, 0, 2222, 2223, 5, 51, 0, 0, 2223, 2224, 5, + 65, 0, 0, 2224, 2341, 5, 49, 0, 0, 2225, 2226, 5, 92, 0, 0, 2226, 2227, 5, 114, 0, 0, + 2227, 2228, 5, 104, 0, 0, 2228, 2341, 5, 111, 0, 0, 2229, 2230, 5, 92, 0, 0, 2230, + 2231, 5, 118, 0, 0, 2231, 2232, 5, 97, 0, 0, 2232, 2233, 5, 114, 0, 0, 2233, 2234, + 5, 114, 0, 0, 2234, 2235, 5, 104, 0, 0, 2235, 2341, 5, 111, 0, 0, 2236, 2237, 5, 92, + 0, 0, 2237, 2238, 5, 83, 0, 0, 2238, 2239, 5, 105, 0, 0, 2239, 2240, 5, 103, 0, 0, 2240, + 2241, 5, 109, 0, 0, 2241, 2341, 5, 97, 0, 0, 2242, 2243, 5, 92, 0, 0, 2243, 2244, 5, + 115, 0, 0, 2244, 2245, 5, 105, 0, 0, 2245, 2246, 5, 103, 0, 0, 2246, 2247, 5, 109, + 0, 0, 2247, 2341, 5, 97, 0, 0, 2248, 2249, 5, 92, 0, 0, 2249, 2250, 5, 118, 0, 0, 2250, + 2251, 5, 97, 0, 0, 2251, 2252, 5, 114, 0, 0, 2252, 2253, 5, 115, 0, 0, 2253, 2254, + 5, 105, 0, 0, 2254, 2255, 5, 103, 0, 0, 2255, 2256, 5, 109, 0, 0, 2256, 2341, 5, 97, + 0, 0, 2257, 2258, 5, 92, 0, 0, 2258, 2259, 5, 99, 0, 0, 2259, 2260, 5, 104, 0, 0, 2260, + 2261, 5, 97, 0, 0, 2261, 2262, 5, 114, 0, 0, 2262, 2263, 5, 34, 0, 0, 2263, 2264, 5, + 48, 0, 0, 2264, 2265, 5, 48, 0, 0, 2265, 2266, 5, 48, 0, 0, 2266, 2267, 5, 51, 0, 0, + 2267, 2268, 5, 65, 0, 0, 2268, 2341, 5, 52, 0, 0, 2269, 2270, 5, 92, 0, 0, 2270, 2271, + 5, 116, 0, 0, 2271, 2272, 5, 97, 0, 0, 2272, 2341, 5, 117, 0, 0, 2273, 2274, 5, 92, + 0, 0, 2274, 2275, 5, 85, 0, 0, 2275, 2276, 5, 112, 0, 0, 2276, 2277, 5, 115, 0, 0, 2277, + 2278, 5, 105, 0, 0, 2278, 2279, 5, 108, 0, 0, 2279, 2280, 5, 111, 0, 0, 2280, 2341, + 5, 110, 0, 0, 2281, 2282, 5, 92, 0, 0, 2282, 2283, 5, 117, 0, 0, 2283, 2284, 5, 112, + 0, 0, 2284, 2285, 5, 115, 0, 0, 2285, 2286, 5, 105, 0, 0, 2286, 2287, 5, 108, 0, 0, + 2287, 2288, 5, 111, 0, 0, 2288, 2341, 5, 110, 0, 0, 2289, 2290, 5, 92, 0, 0, 2290, + 2291, 5, 80, 0, 0, 2291, 2292, 5, 104, 0, 0, 2292, 2341, 5, 105, 0, 0, 2293, 2294, + 5, 92, 0, 0, 2294, 2295, 5, 112, 0, 0, 2295, 2296, 5, 104, 0, 0, 2296, 2341, 5, 105, + 0, 0, 2297, 2298, 5, 92, 0, 0, 2298, 2299, 5, 118, 0, 0, 2299, 2300, 5, 97, 0, 0, 2300, + 2301, 5, 114, 0, 0, 2301, 2302, 5, 112, 0, 0, 2302, 2303, 5, 104, 0, 0, 2303, 2341, + 5, 105, 0, 0, 2304, 2305, 5, 92, 0, 0, 2305, 2306, 5, 99, 0, 0, 2306, 2307, 5, 104, + 0, 0, 2307, 2308, 5, 97, 0, 0, 2308, 2309, 5, 114, 0, 0, 2309, 2310, 5, 34, 0, 0, 2310, + 2311, 5, 48, 0, 0, 2311, 2312, 5, 48, 0, 0, 2312, 2313, 5, 48, 0, 0, 2313, 2314, 5, + 51, 0, 0, 2314, 2315, 5, 65, 0, 0, 2315, 2341, 5, 55, 0, 0, 2316, 2317, 5, 92, 0, 0, + 2317, 2318, 5, 99, 0, 0, 2318, 2319, 5, 104, 0, 0, 2319, 2341, 5, 105, 0, 0, 2320, + 2321, 5, 92, 0, 0, 2321, 2322, 5, 80, 0, 0, 2322, 2323, 5, 115, 0, 0, 2323, 2341, 5, + 105, 0, 0, 2324, 2325, 5, 92, 0, 0, 2325, 2326, 5, 112, 0, 0, 2326, 2327, 5, 115, 0, + 0, 2327, 2341, 5, 105, 0, 0, 2328, 2329, 5, 92, 0, 0, 2329, 2330, 5, 79, 0, 0, 2330, + 2331, 5, 109, 0, 0, 2331, 2332, 5, 101, 0, 0, 2332, 2333, 5, 103, 0, 0, 2333, 2341, + 5, 97, 0, 0, 2334, 2335, 5, 92, 0, 0, 2335, 2336, 5, 111, 0, 0, 2336, 2337, 5, 109, + 0, 0, 2337, 2338, 5, 101, 0, 0, 2338, 2339, 5, 103, 0, 0, 2339, 2341, 5, 97, 0, 0, 2340, + 1955, 1, 0, 0, 0, 2340, 1967, 1, 0, 0, 0, 2340, 1973, 1, 0, 0, 0, 2340, 1985, 1, 0, 0, + 0, 2340, 1990, 1, 0, 0, 0, 2340, 1996, 1, 0, 0, 0, 2340, 2002, 1, 0, 0, 0, 2340, 2008, + 1, 0, 0, 0, 2340, 2014, 1, 0, 0, 0, 2340, 2026, 1, 0, 0, 0, 2340, 2034, 1, 0, 0, 0, 2340, + 2045, 1, 0, 0, 0, 2340, 2057, 1, 0, 0, 0, 2340, 2062, 1, 0, 0, 0, 2340, 2074, 1, 0, 0, + 0, 2340, 2078, 1, 0, 0, 0, 2340, 2084, 1, 0, 0, 0, 2340, 2090, 1, 0, 0, 0, 2340, 2099, + 1, 0, 0, 0, 2340, 2111, 1, 0, 0, 0, 2340, 2116, 1, 0, 0, 0, 2340, 2128, 1, 0, 0, 0, 2340, + 2134, 1, 0, 0, 0, 2340, 2141, 1, 0, 0, 0, 2340, 2148, 1, 0, 0, 0, 2340, 2160, 1, 0, 0, + 0, 2340, 2163, 1, 0, 0, 0, 2340, 2175, 1, 0, 0, 0, 2340, 2178, 1, 0, 0, 0, 2340, 2181, + 1, 0, 0, 0, 2340, 2184, 1, 0, 0, 0, 2340, 2196, 1, 0, 0, 0, 2340, 2204, 1, 0, 0, 0, 2340, + 2207, 1, 0, 0, 0, 2340, 2213, 1, 0, 0, 0, 2340, 2225, 1, 0, 0, 0, 2340, 2229, 1, 0, 0, + 0, 2340, 2236, 1, 0, 0, 0, 2340, 2242, 1, 0, 0, 0, 2340, 2248, 1, 0, 0, 0, 2340, 2257, + 1, 0, 0, 0, 2340, 2269, 1, 0, 0, 0, 2340, 2273, 1, 0, 0, 0, 2340, 2281, 1, 0, 0, 0, 2340, + 2289, 1, 0, 0, 0, 2340, 2293, 1, 0, 0, 0, 2340, 2297, 1, 0, 0, 0, 2340, 2304, 1, 0, 0, + 0, 2340, 2316, 1, 0, 0, 0, 2340, 2320, 1, 0, 0, 0, 2340, 2324, 1, 0, 0, 0, 2340, 2328, + 1, 0, 0, 0, 2340, 2334, 1, 0, 0, 0, 2341, 390, 1, 0, 0, 0, 2342, 2344, 3, 389, 194, 0, + 2343, 2345, 7, 4, 0, 0, 2344, 2343, 1, 0, 0, 0, 2344, 2345, 1, 0, 0, 0, 2345, 392, 1, + 0, 0, 0, 2346, 2347, 5, 92, 0, 0, 2347, 2348, 5, 66, 0, 0, 2348, 2349, 5, 98, 0, 0, 2349, + 2350, 5, 98, 0, 0, 2350, 2697, 5, 107, 0, 0, 2351, 2352, 5, 92, 0, 0, 2352, 2353, 5, + 119, 0, 0, 2353, 2697, 5, 112, 0, 0, 2354, 2355, 5, 92, 0, 0, 2355, 2356, 5, 110, 0, + 0, 2356, 2357, 5, 97, 0, 0, 2357, 2358, 5, 98, 0, 0, 2358, 2359, 5, 108, 0, 0, 2359, + 2697, 5, 97, 0, 0, 2360, 2361, 5, 92, 0, 0, 2361, 2362, 5, 98, 0, 0, 2362, 2363, 5, + 105, 0, 0, 2363, 2364, 5, 103, 0, 0, 2364, 2365, 5, 115, 0, 0, 2365, 2366, 5, 116, + 0, 0, 2366, 2367, 5, 97, 0, 0, 2367, 2697, 5, 114, 0, 0, 2368, 2369, 5, 92, 0, 0, 2369, + 2370, 5, 97, 0, 0, 2370, 2371, 5, 110, 0, 0, 2371, 2372, 5, 103, 0, 0, 2372, 2373, + 5, 108, 0, 0, 2373, 2697, 5, 101, 0, 0, 2374, 2375, 5, 92, 0, 0, 2375, 2376, 5, 110, + 0, 0, 2376, 2377, 5, 101, 0, 0, 2377, 2378, 5, 120, 0, 0, 2378, 2379, 5, 105, 0, 0, + 2379, 2380, 5, 115, 0, 0, 2380, 2381, 5, 116, 0, 0, 2381, 2697, 5, 115, 0, 0, 2382, + 2383, 5, 92, 0, 0, 2383, 2384, 5, 100, 0, 0, 2384, 2385, 5, 105, 0, 0, 2385, 2386, + 5, 97, 0, 0, 2386, 2387, 5, 103, 0, 0, 2387, 2388, 5, 100, 0, 0, 2388, 2389, 5, 111, + 0, 0, 2389, 2390, 5, 119, 0, 0, 2390, 2697, 5, 110, 0, 0, 2391, 2392, 5, 92, 0, 0, 2392, + 2393, 5, 109, 0, 0, 2393, 2394, 5, 101, 0, 0, 2394, 2395, 5, 97, 0, 0, 2395, 2396, + 5, 115, 0, 0, 2396, 2397, 5, 117, 0, 0, 2397, 2398, 5, 114, 0, 0, 2398, 2399, 5, 101, + 0, 0, 2399, 2400, 5, 100, 0, 0, 2400, 2401, 5, 97, 0, 0, 2401, 2402, 5, 110, 0, 0, 2402, + 2403, 5, 103, 0, 0, 2403, 2404, 5, 108, 0, 0, 2404, 2697, 5, 101, 0, 0, 2405, 2406, + 5, 92, 0, 0, 2406, 2407, 5, 101, 0, 0, 2407, 2408, 5, 116, 0, 0, 2408, 2697, 5, 104, + 0, 0, 2409, 2410, 5, 92, 0, 0, 2410, 2411, 5, 101, 0, 0, 2411, 2412, 5, 109, 0, 0, 2412, + 2413, 5, 112, 0, 0, 2413, 2414, 5, 116, 0, 0, 2414, 2415, 5, 121, 0, 0, 2415, 2416, + 5, 115, 0, 0, 2416, 2417, 5, 101, 0, 0, 2417, 2697, 5, 116, 0, 0, 2418, 2419, 5, 92, + 0, 0, 2419, 2420, 5, 100, 0, 0, 2420, 2421, 5, 105, 0, 0, 2421, 2422, 5, 97, 0, 0, 2422, + 2423, 5, 103, 0, 0, 2423, 2424, 5, 117, 0, 0, 2424, 2697, 5, 112, 0, 0, 2425, 2426, + 5, 92, 0, 0, 2426, 2427, 5, 115, 0, 0, 2427, 2428, 5, 112, 0, 0, 2428, 2429, 5, 104, + 0, 0, 2429, 2430, 5, 101, 0, 0, 2430, 2431, 5, 114, 0, 0, 2431, 2432, 5, 105, 0, 0, + 2432, 2433, 5, 99, 0, 0, 2433, 2434, 5, 97, 0, 0, 2434, 2435, 5, 108, 0, 0, 2435, 2436, + 5, 97, 0, 0, 2436, 2437, 5, 110, 0, 0, 2437, 2438, 5, 103, 0, 0, 2438, 2439, 5, 108, + 0, 0, 2439, 2697, 5, 101, 0, 0, 2440, 2441, 5, 92, 0, 0, 2441, 2442, 5, 99, 0, 0, 2442, + 2443, 5, 108, 0, 0, 2443, 2444, 5, 117, 0, 0, 2444, 2445, 5, 98, 0, 0, 2445, 2446, + 5, 115, 0, 0, 2446, 2447, 5, 117, 0, 0, 2447, 2448, 5, 105, 0, 0, 2448, 2697, 5, 116, + 0, 0, 2449, 2450, 5, 92, 0, 0, 2450, 2451, 5, 118, 0, 0, 2451, 2452, 5, 97, 0, 0, 2452, + 2453, 5, 114, 0, 0, 2453, 2454, 5, 110, 0, 0, 2454, 2455, 5, 111, 0, 0, 2455, 2456, + 5, 116, 0, 0, 2456, 2457, 5, 104, 0, 0, 2457, 2458, 5, 105, 0, 0, 2458, 2459, 5, 110, + 0, 0, 2459, 2697, 5, 103, 0, 0, 2460, 2461, 5, 92, 0, 0, 2461, 2462, 5, 68, 0, 0, 2462, + 2463, 5, 105, 0, 0, 2463, 2464, 5, 97, 0, 0, 2464, 2465, 5, 109, 0, 0, 2465, 2466, + 5, 111, 0, 0, 2466, 2467, 5, 110, 0, 0, 2467, 2697, 5, 100, 0, 0, 2468, 2469, 5, 92, + 0, 0, 2469, 2470, 5, 99, 0, 0, 2470, 2471, 5, 111, 0, 0, 2471, 2472, 5, 109, 0, 0, 2472, + 2473, 5, 112, 0, 0, 2473, 2474, 5, 108, 0, 0, 2474, 2475, 5, 101, 0, 0, 2475, 2476, + 5, 109, 0, 0, 2476, 2477, 5, 101, 0, 0, 2477, 2478, 5, 110, 0, 0, 2478, 2697, 5, 116, + 0, 0, 2479, 2480, 5, 92, 0, 0, 2480, 2481, 5, 100, 0, 0, 2481, 2482, 5, 105, 0, 0, 2482, + 2483, 5, 97, 0, 0, 2483, 2484, 5, 109, 0, 0, 2484, 2485, 5, 111, 0, 0, 2485, 2486, + 5, 110, 0, 0, 2486, 2487, 5, 100, 0, 0, 2487, 2488, 5, 115, 0, 0, 2488, 2489, 5, 117, + 0, 0, 2489, 2490, 5, 105, 0, 0, 2490, 2697, 5, 116, 0, 0, 2491, 2492, 5, 92, 0, 0, 2492, + 2493, 5, 105, 0, 0, 2493, 2494, 5, 109, 0, 0, 2494, 2495, 5, 97, 0, 0, 2495, 2496, + 5, 116, 0, 0, 2496, 2697, 5, 104, 0, 0, 2497, 2498, 5, 92, 0, 0, 2498, 2499, 5, 70, + 0, 0, 2499, 2500, 5, 105, 0, 0, 2500, 2501, 5, 110, 0, 0, 2501, 2697, 5, 118, 0, 0, + 2502, 2503, 5, 92, 0, 0, 2503, 2504, 5, 116, 0, 0, 2504, 2505, 5, 114, 0, 0, 2505, + 2506, 5, 105, 0, 0, 2506, 2507, 5, 97, 0, 0, 2507, 2508, 5, 110, 0, 0, 2508, 2509, + 5, 103, 0, 0, 2509, 2510, 5, 108, 0, 0, 2510, 2511, 5, 101, 0, 0, 2511, 2512, 5, 100, + 0, 0, 2512, 2513, 5, 111, 0, 0, 2513, 2514, 5, 119, 0, 0, 2514, 2697, 5, 110, 0, 0, + 2515, 2516, 5, 92, 0, 0, 2516, 2517, 5, 104, 0, 0, 2517, 2518, 5, 101, 0, 0, 2518, + 2519, 5, 97, 0, 0, 2519, 2520, 5, 114, 0, 0, 2520, 2521, 5, 116, 0, 0, 2521, 2522, + 5, 115, 0, 0, 2522, 2523, 5, 117, 0, 0, 2523, 2524, 5, 105, 0, 0, 2524, 2697, 5, 116, + 0, 0, 2525, 2526, 5, 92, 0, 0, 2526, 2527, 5, 106, 0, 0, 2527, 2528, 5, 109, 0, 0, 2528, + 2529, 5, 97, 0, 0, 2529, 2530, 5, 116, 0, 0, 2530, 2697, 5, 104, 0, 0, 2531, 2532, + 5, 92, 0, 0, 2532, 2533, 5, 71, 0, 0, 2533, 2534, 5, 97, 0, 0, 2534, 2535, 5, 109, 0, + 0, 2535, 2697, 5, 101, 0, 0, 2536, 2537, 5, 92, 0, 0, 2537, 2538, 5, 116, 0, 0, 2538, + 2539, 5, 114, 0, 0, 2539, 2540, 5, 105, 0, 0, 2540, 2541, 5, 97, 0, 0, 2541, 2542, + 5, 110, 0, 0, 2542, 2543, 5, 103, 0, 0, 2543, 2544, 5, 108, 0, 0, 2544, 2697, 5, 101, + 0, 0, 2545, 2546, 5, 92, 0, 0, 2546, 2547, 5, 115, 0, 0, 2547, 2548, 5, 112, 0, 0, 2548, + 2549, 5, 97, 0, 0, 2549, 2550, 5, 100, 0, 0, 2550, 2551, 5, 101, 0, 0, 2551, 2552, + 5, 115, 0, 0, 2552, 2553, 5, 117, 0, 0, 2553, 2554, 5, 105, 0, 0, 2554, 2697, 5, 116, + 0, 0, 2555, 2556, 5, 92, 0, 0, 2556, 2557, 5, 101, 0, 0, 2557, 2558, 5, 108, 0, 0, 2558, + 2697, 5, 108, 0, 0, 2559, 2560, 5, 92, 0, 0, 2560, 2561, 5, 104, 0, 0, 2561, 2562, + 5, 98, 0, 0, 2562, 2563, 5, 97, 0, 0, 2563, 2697, 5, 114, 0, 0, 2564, 2565, 5, 92, 0, + 0, 2565, 2566, 5, 118, 0, 0, 2566, 2567, 5, 97, 0, 0, 2567, 2568, 5, 114, 0, 0, 2568, + 2569, 5, 116, 0, 0, 2569, 2570, 5, 114, 0, 0, 2570, 2571, 5, 105, 0, 0, 2571, 2572, + 5, 97, 0, 0, 2572, 2573, 5, 110, 0, 0, 2573, 2574, 5, 103, 0, 0, 2574, 2575, 5, 108, + 0, 0, 2575, 2697, 5, 101, 0, 0, 2576, 2577, 5, 92, 0, 0, 2577, 2578, 5, 104, 0, 0, 2578, + 2579, 5, 115, 0, 0, 2579, 2580, 5, 108, 0, 0, 2580, 2581, 5, 97, 0, 0, 2581, 2582, + 5, 115, 0, 0, 2582, 2697, 5, 104, 0, 0, 2583, 2584, 5, 92, 0, 0, 2584, 2585, 5, 98, + 0, 0, 2585, 2586, 5, 108, 0, 0, 2586, 2587, 5, 97, 0, 0, 2587, 2588, 5, 99, 0, 0, 2588, + 2589, 5, 107, 0, 0, 2589, 2590, 5, 108, 0, 0, 2590, 2591, 5, 111, 0, 0, 2591, 2592, + 5, 122, 0, 0, 2592, 2593, 5, 101, 0, 0, 2593, 2594, 5, 110, 0, 0, 2594, 2595, 5, 103, + 0, 0, 2595, 2697, 5, 101, 0, 0, 2596, 2597, 5, 92, 0, 0, 2597, 2598, 5, 108, 0, 0, 2598, + 2599, 5, 111, 0, 0, 2599, 2600, 5, 122, 0, 0, 2600, 2601, 5, 101, 0, 0, 2601, 2602, + 5, 110, 0, 0, 2602, 2603, 5, 103, 0, 0, 2603, 2697, 5, 101, 0, 0, 2604, 2605, 5, 92, + 0, 0, 2605, 2606, 5, 98, 0, 0, 2606, 2607, 5, 108, 0, 0, 2607, 2608, 5, 97, 0, 0, 2608, + 2609, 5, 99, 0, 0, 2609, 2610, 5, 107, 0, 0, 2610, 2611, 5, 115, 0, 0, 2611, 2612, + 5, 113, 0, 0, 2612, 2613, 5, 117, 0, 0, 2613, 2614, 5, 97, 0, 0, 2614, 2615, 5, 114, + 0, 0, 2615, 2697, 5, 101, 0, 0, 2616, 2617, 5, 92, 0, 0, 2617, 2618, 5, 109, 0, 0, 2618, + 2619, 5, 104, 0, 0, 2619, 2697, 5, 111, 0, 0, 2620, 2621, 5, 92, 0, 0, 2621, 2622, + 5, 98, 0, 0, 2622, 2623, 5, 108, 0, 0, 2623, 2624, 5, 97, 0, 0, 2624, 2625, 5, 99, 0, + 0, 2625, 2626, 5, 107, 0, 0, 2626, 2627, 5, 116, 0, 0, 2627, 2628, 5, 114, 0, 0, 2628, + 2629, 5, 105, 0, 0, 2629, 2630, 5, 97, 0, 0, 2630, 2631, 5, 110, 0, 0, 2631, 2632, + 5, 103, 0, 0, 2632, 2633, 5, 108, 0, 0, 2633, 2697, 5, 101, 0, 0, 2634, 2635, 5, 92, + 0, 0, 2635, 2636, 5, 115, 0, 0, 2636, 2637, 5, 104, 0, 0, 2637, 2638, 5, 97, 0, 0, 2638, + 2639, 5, 114, 0, 0, 2639, 2697, 5, 112, 0, 0, 2640, 2641, 5, 92, 0, 0, 2641, 2642, + 5, 112, 0, 0, 2642, 2643, 5, 114, 0, 0, 2643, 2644, 5, 105, 0, 0, 2644, 2645, 5, 109, + 0, 0, 2645, 2697, 5, 101, 0, 0, 2646, 2647, 5, 92, 0, 0, 2647, 2648, 5, 73, 0, 0, 2648, + 2697, 5, 109, 0, 0, 2649, 2650, 5, 92, 0, 0, 2650, 2651, 5, 102, 0, 0, 2651, 2652, + 5, 108, 0, 0, 2652, 2653, 5, 97, 0, 0, 2653, 2697, 5, 116, 0, 0, 2654, 2655, 5, 92, + 0, 0, 2655, 2656, 5, 115, 0, 0, 2656, 2657, 5, 113, 0, 0, 2657, 2658, 5, 117, 0, 0, + 2658, 2659, 5, 97, 0, 0, 2659, 2660, 5, 114, 0, 0, 2660, 2697, 5, 101, 0, 0, 2661, + 2662, 5, 92, 0, 0, 2662, 2663, 5, 98, 0, 0, 2663, 2664, 5, 97, 0, 0, 2664, 2665, 5, + 99, 0, 0, 2665, 2666, 5, 107, 0, 0, 2666, 2667, 5, 112, 0, 0, 2667, 2668, 5, 114, 0, + 0, 2668, 2669, 5, 105, 0, 0, 2669, 2670, 5, 109, 0, 0, 2670, 2697, 5, 101, 0, 0, 2671, + 2672, 5, 92, 0, 0, 2672, 2673, 5, 82, 0, 0, 2673, 2697, 5, 101, 0, 0, 2674, 2675, 5, + 92, 0, 0, 2675, 2676, 5, 110, 0, 0, 2676, 2677, 5, 97, 0, 0, 2677, 2678, 5, 116, 0, + 0, 2678, 2679, 5, 117, 0, 0, 2679, 2680, 5, 114, 0, 0, 2680, 2681, 5, 97, 0, 0, 2681, + 2697, 5, 108, 0, 0, 2682, 2683, 5, 92, 0, 0, 2683, 2684, 5, 115, 0, 0, 2684, 2685, + 5, 117, 0, 0, 2685, 2686, 5, 114, 0, 0, 2686, 2697, 5, 100, 0, 0, 2687, 2688, 5, 92, + 0, 0, 2688, 2689, 5, 99, 0, 0, 2689, 2690, 5, 105, 0, 0, 2690, 2691, 5, 114, 0, 0, 2691, + 2692, 5, 99, 0, 0, 2692, 2693, 5, 108, 0, 0, 2693, 2694, 5, 101, 0, 0, 2694, 2695, + 5, 100, 0, 0, 2695, 2697, 5, 83, 0, 0, 2696, 2346, 1, 0, 0, 0, 2696, 2351, 1, 0, 0, 0, + 2696, 2354, 1, 0, 0, 0, 2696, 2360, 1, 0, 0, 0, 2696, 2368, 1, 0, 0, 0, 2696, 2374, + 1, 0, 0, 0, 2696, 2382, 1, 0, 0, 0, 2696, 2391, 1, 0, 0, 0, 2696, 2405, 1, 0, 0, 0, 2696, + 2409, 1, 0, 0, 0, 2696, 2418, 1, 0, 0, 0, 2696, 2425, 1, 0, 0, 0, 2696, 2440, 1, 0, 0, + 0, 2696, 2449, 1, 0, 0, 0, 2696, 2460, 1, 0, 0, 0, 2696, 2468, 1, 0, 0, 0, 2696, 2479, + 1, 0, 0, 0, 2696, 2491, 1, 0, 0, 0, 2696, 2497, 1, 0, 0, 0, 2696, 2502, 1, 0, 0, 0, 2696, + 2515, 1, 0, 0, 0, 2696, 2525, 1, 0, 0, 0, 2696, 2531, 1, 0, 0, 0, 2696, 2536, 1, 0, 0, + 0, 2696, 2545, 1, 0, 0, 0, 2696, 2555, 1, 0, 0, 0, 2696, 2559, 1, 0, 0, 0, 2696, 2564, + 1, 0, 0, 0, 2696, 2576, 1, 0, 0, 0, 2696, 2583, 1, 0, 0, 0, 2696, 2596, 1, 0, 0, 0, 2696, + 2604, 1, 0, 0, 0, 2696, 2616, 1, 0, 0, 0, 2696, 2620, 1, 0, 0, 0, 2696, 2634, 1, 0, 0, + 0, 2696, 2640, 1, 0, 0, 0, 2696, 2646, 1, 0, 0, 0, 2696, 2649, 1, 0, 0, 0, 2696, 2654, + 1, 0, 0, 0, 2696, 2661, 1, 0, 0, 0, 2696, 2671, 1, 0, 0, 0, 2696, 2674, 1, 0, 0, 0, 2696, + 2682, 1, 0, 0, 0, 2696, 2687, 1, 0, 0, 0, 2697, 394, 1, 0, 0, 0, 2698, 2700, 3, 393, + 196, 0, 2699, 2701, 7, 4, 0, 0, 2700, 2699, 1, 0, 0, 0, 2700, 2701, 1, 0, 0, 0, 2701, + 396, 1, 0, 0, 0, 2702, 2703, 5, 92, 0, 0, 2703, 2704, 5, 112, 0, 0, 2704, 2705, 5, 105, + 0, 0, 2705, 398, 1, 0, 0, 0, 2706, 2707, 5, 92, 0, 0, 2707, 2708, 5, 105, 0, 0, 2708, + 2709, 5, 110, 0, 0, 2709, 2710, 5, 102, 0, 0, 2710, 2711, 5, 116, 0, 0, 2711, 2712, + 5, 121, 0, 0, 2712, 400, 1, 0, 0, 0, 2713, 2714, 5, 92, 0, 0, 2714, 2715, 5, 112, 0, + 0, 2715, 2716, 5, 97, 0, 0, 2716, 2717, 5, 114, 0, 0, 2717, 2718, 5, 116, 0, 0, 2718, + 2719, 5, 105, 0, 0, 2719, 2720, 5, 97, 0, 0, 2720, 2721, 5, 108, 0, 0, 2721, 402, 1, + 0, 0, 0, 2722, 2730, 3, 399, 199, 0, 2723, 2724, 3, 91, 45, 0, 2724, 2725, 3, 399, + 199, 0, 2725, 2730, 1, 0, 0, 0, 2726, 2727, 3, 399, 199, 0, 2727, 2728, 3, 385, 192, + 0, 2728, 2730, 1, 0, 0, 0, 2729, 2722, 1, 0, 0, 0, 2729, 2723, 1, 0, 0, 0, 2729, 2726, + 1, 0, 0, 0, 2730, 404, 1, 0, 0, 0, 2731, 2732, 5, 92, 0, 0, 2732, 2733, 5, 101, 0, 0, + 2733, 2734, 5, 109, 0, 0, 2734, 2735, 5, 112, 0, 0, 2735, 2736, 5, 116, 0, 0, 2736, + 2737, 5, 121, 0, 0, 2737, 2738, 5, 115, 0, 0, 2738, 2739, 5, 101, 0, 0, 2739, 2740, + 5, 116, 0, 0, 2740, 406, 1, 0, 0, 0, 2741, 2746, 3, 397, 198, 0, 2742, 2746, 3, 401, + 200, 0, 2743, 2746, 3, 403, 201, 0, 2744, 2746, 3, 405, 202, 0, 2745, 2741, 1, 0, + 0, 0, 2745, 2742, 1, 0, 0, 0, 2745, 2743, 1, 0, 0, 0, 2745, 2744, 1, 0, 0, 0, 2746, 408, + 1, 0, 0, 0, 2747, 2748, 5, 92, 0, 0, 2748, 2749, 5, 118, 0, 0, 2749, 2750, 5, 97, 0, + 0, 2750, 2751, 5, 114, 0, 0, 2751, 2752, 5, 105, 0, 0, 2752, 2753, 5, 97, 0, 0, 2753, + 2754, 5, 98, 0, 0, 2754, 2755, 5, 108, 0, 0, 2755, 2756, 5, 101, 0, 0, 2756, 410, 1, + 0, 0, 0, 2757, 2762, 3, 391, 195, 0, 2758, 2762, 3, 395, 197, 0, 2759, 2762, 3, 355, + 177, 0, 2760, 2762, 3, 357, 178, 0, 2761, 2757, 1, 0, 0, 0, 2761, 2758, 1, 0, 0, 0, + 2761, 2759, 1, 0, 0, 0, 2761, 2760, 1, 0, 0, 0, 2762, 2763, 1, 0, 0, 0, 2763, 2761, + 1, 0, 0, 0, 2763, 2764, 1, 0, 0, 0, 2764, 2786, 1, 0, 0, 0, 2765, 2784, 3, 333, 166, + 0, 2766, 2772, 3, 109, 54, 0, 2767, 2773, 3, 391, 195, 0, 2768, 2773, 3, 395, 197, + 0, 2769, 2773, 3, 355, 177, 0, 2770, 2773, 3, 357, 178, 0, 2771, 2773, 3, 341, 170, + 0, 2772, 2767, 1, 0, 0, 0, 2772, 2768, 1, 0, 0, 0, 2772, 2769, 1, 0, 0, 0, 2772, 2770, + 1, 0, 0, 0, 2772, 2771, 1, 0, 0, 0, 2773, 2774, 1, 0, 0, 0, 2774, 2772, 1, 0, 0, 0, 2774, + 2775, 1, 0, 0, 0, 2775, 2776, 1, 0, 0, 0, 2776, 2777, 3, 111, 55, 0, 2777, 2785, 1, + 0, 0, 0, 2778, 2783, 3, 391, 195, 0, 2779, 2783, 3, 395, 197, 0, 2780, 2783, 3, 355, + 177, 0, 2781, 2783, 3, 357, 178, 0, 2782, 2778, 1, 0, 0, 0, 2782, 2779, 1, 0, 0, 0, + 2782, 2780, 1, 0, 0, 0, 2782, 2781, 1, 0, 0, 0, 2783, 2785, 1, 0, 0, 0, 2784, 2766, + 1, 0, 0, 0, 2784, 2782, 1, 0, 0, 0, 2785, 2787, 1, 0, 0, 0, 2786, 2765, 1, 0, 0, 0, 2786, + 2787, 1, 0, 0, 0, 2787, 412, 1, 0, 0, 0, 2788, 2789, 3, 409, 204, 0, 2789, 2790, 3, + 109, 54, 0, 2790, 2791, 3, 411, 205, 0, 2791, 2793, 3, 111, 55, 0, 2792, 2794, 3, + 385, 192, 0, 2793, 2792, 1, 0, 0, 0, 2793, 2794, 1, 0, 0, 0, 2794, 414, 1, 0, 0, 0, 44, + 0, 791, 812, 1063, 1397, 1450, 1481, 1503, 1527, 1535, 1581, 1652, 1717, 1725, + 1727, 1743, 1777, 1815, 1820, 1829, 1835, 1845, 1852, 1854, 1860, 1865, 1881, + 1901, 1921, 1945, 2340, 2344, 2696, 2700, 2729, 2745, 2761, 2763, 2772, 2774, + 2782, 2784, 2786, 2793, 1, 6, 0, 0 + ] + + +class PSLexer(Lexer): + + atn = ATNDeserializer().deserialize(serializedATN()) + + decisionsToDFA = [DFA(ds, i) for i, ds in enumerate(atn.decisionToState)] + + T__0 = 1 + T__1 = 2 + T__2 = 3 + T__3 = 4 + T__4 = 5 + T__5 = 6 + T__6 = 7 + T__7 = 8 + T__8 = 9 + T__9 = 10 + T__10 = 11 + T__11 = 12 + T__12 = 13 + T__13 = 14 + T__14 = 15 + T__15 = 16 + T__16 = 17 + T__17 = 18 + T__18 = 19 + T__19 = 20 + T__20 = 21 + T__21 = 22 + T__22 = 23 + T__23 = 24 + T__24 = 25 + T__25 = 26 + T__26 = 27 + T__27 = 28 + T__28 = 29 + T__29 = 30 + T__30 = 31 + T__31 = 32 + T__32 = 33 + T__33 = 34 + T__34 = 35 + T__35 = 36 + T__36 = 37 + T__37 = 38 + T__38 = 39 + T__39 = 40 + T__40 = 41 + T__41 = 42 + T__42 = 43 + T__43 = 44 + WS = 45 + DOLLAR_SIGN = 46 + ADD = 47 + SUB = 48 + MUL = 49 + DIV = 50 + L_PAREN = 51 + R_PAREN = 52 + L_GROUP = 53 + R_GROUP = 54 + L_BRACE = 55 + R_BRACE = 56 + L_BRACE_VISUAL = 57 + R_BRACE_VISUAL = 58 + L_BRACE_CMD = 59 + R_BRACE_CMD = 60 + L_BRACKET = 61 + R_BRACKET = 62 + L_BRACK = 63 + R_BRACK = 64 + BAR = 65 + L_VERT = 66 + R_VERT = 67 + VERT = 68 + NORM = 69 + L_FLOOR = 70 + R_FLOOR = 71 + LL_CORNER = 72 + LR_CORNER = 73 + L_CEIL = 74 + R_CEIL = 75 + UL_CORNER = 76 + UR_CORNER = 77 + L_LEFT = 78 + R_RIGHT = 79 + ML_LEFT = 80 + MR_RIGHT = 81 + FUNC_LIM = 82 + LIM_APPROACH_SYM = 83 + FUNC_INT = 84 + FUNC_SUM = 85 + FUNC_PROD = 86 + FUNC_LOG = 87 + FUNC_LN = 88 + FUNC_EXP = 89 + FUNC_SIN = 90 + FUNC_COS = 91 + FUNC_TAN = 92 + FUNC_CSC = 93 + FUNC_SEC = 94 + FUNC_COT = 95 + FUNC_ARCSIN = 96 + FUNC_ARCCOS = 97 + FUNC_ARCTAN = 98 + FUNC_ARCCSC = 99 + FUNC_ARCSEC = 100 + FUNC_ARCCOT = 101 + FUNC_SINH = 102 + FUNC_COSH = 103 + FUNC_TANH = 104 + FUNC_ARSINH = 105 + FUNC_ARCOSH = 106 + FUNC_ARTANH = 107 + FUNC_ARCSINH = 108 + FUNC_ARCCOSH = 109 + FUNC_ARCTANH = 110 + FUNC_ARSINH_NAME = 111 + FUNC_ARCSINH_NAME = 112 + FUNC_ARCOSH_NAME = 113 + FUNC_ARCCOSH_NAME = 114 + FUNC_ARTANH_NAME = 115 + FUNC_ARCTANH_NAME = 116 + FUNC_GCD_NAME = 117 + FUNC_LCM_NAME = 118 + FUNC_FLOOR_NAME = 119 + FUNC_CEIL_NAME = 120 + FUNC_SQRT = 121 + FUNC_GCD = 122 + FUNC_LCM = 123 + FUNC_FLOOR = 124 + FUNC_CEIL = 125 + FUNC_MAX = 126 + FUNC_MIN = 127 + FUNC_DET = 128 + FUNC_EYE_NAME = 129 + FUNC_ZEROS_NAME = 130 + FUNC_ONES_NAME = 131 + FUNC_COLS_NAME = 132 + FUNC_ROWS_NAME = 133 + FUNC_DIAG_NAME = 134 + FUNC_NORM_NAME = 135 + FUNC_RANK_NAME = 136 + FUNC_TRACE_NAME = 137 + FUNC_RREF_NAME = 138 + FUNC_HSTACK_NAME = 139 + FUNC_VSTACK_NAME = 140 + FUNC_ORTHOGONALIZE_NAME = 141 + FUNC_NULLSPACE_NAME = 142 + FUNC_DIAGONALIZE_NAME = 143 + FUNC_EIGENVALS_NAME = 144 + FUNC_EIGENVECTORS_NAME = 145 + FUNC_SVD_NAME = 146 + CMD_TIMES = 147 + CMD_CDOT = 148 + CMD_DIV = 149 + CMD_FRAC = 150 + CMD_BINOM = 151 + CMD_CHOOSE = 152 + CMD_MOD = 153 + CMD_MATHIT = 154 + CMD_OPERATORNAME = 155 + MATRIX_TYPE_MATRIX = 156 + MATRIX_TYPE_PMATRIX = 157 + MATRIX_TYPE_BMATRIX = 158 + MATRIX_TYPE_DET = 159 + MATRIX_TYPES = 160 + CMD_MATRIX_START = 161 + CMD_MATRIX_END = 162 + CMD_DET_START = 163 + CMD_DET_END = 164 + MATRIX_DEL_COL = 165 + MATRIX_DEL_ROW = 166 + UNDERSCORE = 167 + CARET = 168 + COLON = 169 + SEMICOLON = 170 + COMMA = 171 + PERIOD = 172 + DIFFERENTIAL = 173 + EXP_E = 174 + E_NOTATION_E = 175 + LETTER_NO_E = 176 + MATRIX_XRIGHTARROW = 177 + TRANSFORM_EXCHANGE = 178 + NUMBER = 179 + E_NOTATION = 180 + IN = 181 + ASSIGNMENT = 182 + EQUAL = 183 + LT = 184 + LTE = 185 + GT = 186 + GTE = 187 + UNEQUAL = 188 + BANG = 189 + PERCENT_NUMBER = 190 + GREEK_CMD = 191 + OTHER_SYMBOL_CMD = 192 + SYMBOL = 193 + VARIABLE = 194 + + channelNames = [u"DEFAULT_TOKEN_CHANNEL", u"HIDDEN"] + + modeNames = [u"DEFAULT_MODE"] + + literalNames = [u"<INVALID>", + u"'\\acute'", u"'\\bar'", u"'\\overline'", u"'\\breve'", u"'\\check'", + u"'\\widecheck'", u"'\\dot'", u"'\\ddot'", u"'\\grave'", u"'\\hat'", + u"'\\tilde'", u"'\\widetilde'", u"'\\vec'", u"'\\overrightarrow'", + u"'\\bm'", u"'\\boldsymbol'", u"'\\text'", u"'\\textit'", u"'\\mathbb'", + u"'\\mathbin'", u"'\\mathbf'", u"'\\mathcal'", u"'\\mathclap'", + u"'\\mathclose'", u"'\\mathellipsis'", u"'\\mathfrak'", u"'\\mathinner'", + u"'\\mathnormal'", u"'\\mathop'", u"'\\mathopen'", u"'\\mathord'", + u"'\\mathpunct'", u"'\\mathrel'", u"'\\mathring'", u"'\\mathrlap'", + u"'\\mathrm'", u"'\\mathscr'", u"'\\mathsf'", u"'\\mathsterling'", + u"'\\mathtt'", u"'^T'", u"'^{T}'", u"'^{\\top}'", u"'''", u"'\\$'", + u"'+'", u"'-'", u"'*'", u"'('", u"')'", u"'\\lgroup'", u"'\\rgroup'", + u"'{'", u"'}'", u"'\\{'", u"'\\}'", u"'\\lbrace'", u"'\\rbrace'", + u"'['", u"']'", u"'\\lbrack'", u"'\\rbrack'", u"'|'", u"'\\lvert'", + u"'\\rvert'", u"'\\vert'", u"'\\|'", u"'\\lfloor'", u"'\\rfloor'", + u"'\\llcorner'", u"'\\lrcorner'", u"'\\lceil'", u"'\\rceil'", + u"'\\ulcorner'", u"'\\urcorner'", u"'\\left'", u"'\\right'", + u"'\\mleft'", u"'\\mright'", u"'\\lim'", u"'\\int'", u"'\\sum'", + u"'\\prod'", u"'\\log'", u"'\\ln'", u"'\\exp'", u"'\\sin'", + u"'\\cos'", u"'\\tan'", u"'\\csc'", u"'\\sec'", u"'\\cot'", + u"'\\arcsin'", u"'\\arccos'", u"'\\arctan'", u"'\\arccsc'", + u"'\\arcsec'", u"'\\arccot'", u"'\\sinh'", u"'\\cosh'", u"'\\tanh'", + u"'\\arsinh'", u"'\\arcosh'", u"'\\artanh'", u"'\\arcsinh'", + u"'\\arccosh'", u"'\\arctanh'", u"'arsinh'", u"'arcsinh'", u"'arcosh'", + u"'arccosh'", u"'artanh'", u"'arctanh'", u"'gcd'", u"'lcm'", + u"'floor'", u"'ceil'", u"'\\sqrt'", u"'\\gcd'", u"'\\lcm'", + u"'\\floor'", u"'\\ceil'", u"'\\max'", u"'\\min'", u"'\\det'", + u"'eye'", u"'zeros'", u"'ones'", u"'cols'", u"'rows'", u"'diag'", + u"'norm'", u"'rank'", u"'rref'", u"'hstack'", u"'vstack'", u"'nullspace'", + u"'\\times'", u"'\\cdot'", u"'\\div'", u"'\\frac'", u"'\\choose'", + u"'\\mod'", u"'\\mathit'", u"'\\operatorname'", u"'matrix'", + u"'pmatrix'", u"'bmatrix'", u"'vmatrix'", u"'&'", u"'\\\\'", + u"'_'", u"'^'", u"':'", u"';'", u"','", u"'.'", u"'E'", u"'\\in'", + u"'='", u"'<'", u"'>'", u"'!'"] + + symbolicNames = [u"<INVALID>", + u"WS", u"DOLLAR_SIGN", u"ADD", u"SUB", u"MUL", u"DIV", u"L_PAREN", + u"R_PAREN", u"L_GROUP", u"R_GROUP", u"L_BRACE", u"R_BRACE", + u"L_BRACE_VISUAL", u"R_BRACE_VISUAL", u"L_BRACE_CMD", u"R_BRACE_CMD", + u"L_BRACKET", u"R_BRACKET", u"L_BRACK", u"R_BRACK", u"BAR", + u"L_VERT", u"R_VERT", u"VERT", u"NORM", u"L_FLOOR", u"R_FLOOR", + u"LL_CORNER", u"LR_CORNER", u"L_CEIL", u"R_CEIL", u"UL_CORNER", + u"UR_CORNER", u"L_LEFT", u"R_RIGHT", u"ML_LEFT", u"MR_RIGHT", + u"FUNC_LIM", u"LIM_APPROACH_SYM", u"FUNC_INT", u"FUNC_SUM", + u"FUNC_PROD", u"FUNC_LOG", u"FUNC_LN", u"FUNC_EXP", u"FUNC_SIN", + u"FUNC_COS", u"FUNC_TAN", u"FUNC_CSC", u"FUNC_SEC", u"FUNC_COT", + u"FUNC_ARCSIN", u"FUNC_ARCCOS", u"FUNC_ARCTAN", u"FUNC_ARCCSC", + u"FUNC_ARCSEC", u"FUNC_ARCCOT", u"FUNC_SINH", u"FUNC_COSH", + u"FUNC_TANH", u"FUNC_ARSINH", u"FUNC_ARCOSH", u"FUNC_ARTANH", + u"FUNC_ARCSINH", u"FUNC_ARCCOSH", u"FUNC_ARCTANH", u"FUNC_ARSINH_NAME", + u"FUNC_ARCSINH_NAME", u"FUNC_ARCOSH_NAME", u"FUNC_ARCCOSH_NAME", + u"FUNC_ARTANH_NAME", u"FUNC_ARCTANH_NAME", u"FUNC_GCD_NAME", + u"FUNC_LCM_NAME", u"FUNC_FLOOR_NAME", u"FUNC_CEIL_NAME", u"FUNC_SQRT", + u"FUNC_GCD", u"FUNC_LCM", u"FUNC_FLOOR", u"FUNC_CEIL", u"FUNC_MAX", + u"FUNC_MIN", u"FUNC_DET", u"FUNC_EYE_NAME", u"FUNC_ZEROS_NAME", + u"FUNC_ONES_NAME", u"FUNC_COLS_NAME", u"FUNC_ROWS_NAME", u"FUNC_DIAG_NAME", + u"FUNC_NORM_NAME", u"FUNC_RANK_NAME", u"FUNC_TRACE_NAME", u"FUNC_RREF_NAME", + u"FUNC_HSTACK_NAME", u"FUNC_VSTACK_NAME", u"FUNC_ORTHOGONALIZE_NAME", + u"FUNC_NULLSPACE_NAME", u"FUNC_DIAGONALIZE_NAME", u"FUNC_EIGENVALS_NAME", + u"FUNC_EIGENVECTORS_NAME", u"FUNC_SVD_NAME", u"CMD_TIMES", u"CMD_CDOT", + u"CMD_DIV", u"CMD_FRAC", u"CMD_BINOM", u"CMD_CHOOSE", u"CMD_MOD", + u"CMD_MATHIT", u"CMD_OPERATORNAME", u"MATRIX_TYPE_MATRIX", u"MATRIX_TYPE_PMATRIX", + u"MATRIX_TYPE_BMATRIX", u"MATRIX_TYPE_DET", u"MATRIX_TYPES", + u"CMD_MATRIX_START", u"CMD_MATRIX_END", u"CMD_DET_START", u"CMD_DET_END", + u"MATRIX_DEL_COL", u"MATRIX_DEL_ROW", u"UNDERSCORE", u"CARET", + u"COLON", u"SEMICOLON", u"COMMA", u"PERIOD", u"DIFFERENTIAL", + u"EXP_E", u"E_NOTATION_E", u"LETTER_NO_E", u"MATRIX_XRIGHTARROW", + u"TRANSFORM_EXCHANGE", u"NUMBER", u"E_NOTATION", u"IN", u"ASSIGNMENT", + u"EQUAL", u"LT", u"LTE", u"GT", u"GTE", u"UNEQUAL", u"BANG", + u"PERCENT_NUMBER", u"GREEK_CMD", u"OTHER_SYMBOL_CMD", u"SYMBOL", + u"VARIABLE"] + + ruleNames = [u"T__0", u"T__1", u"T__2", u"T__3", u"T__4", u"T__5", + u"T__6", u"T__7", u"T__8", u"T__9", u"T__10", u"T__11", + u"T__12", u"T__13", u"T__14", u"T__15", u"T__16", u"T__17", + u"T__18", u"T__19", u"T__20", u"T__21", u"T__22", u"T__23", + u"T__24", u"T__25", u"T__26", u"T__27", u"T__28", u"T__29", + u"T__30", u"T__31", u"T__32", u"T__33", u"T__34", u"T__35", + u"T__36", u"T__37", u"T__38", u"T__39", u"T__40", u"T__41", + u"T__42", u"T__43", u"WS", u"DOLLAR_SIGN", u"ADD", u"SUB", + u"MUL", u"DIV", u"L_PAREN", u"R_PAREN", u"L_GROUP", u"R_GROUP", + u"L_BRACE", u"R_BRACE", u"L_BRACE_VISUAL", u"R_BRACE_VISUAL", + u"L_BRACE_CMD", u"R_BRACE_CMD", u"L_BRACKET", u"R_BRACKET", + u"L_BRACK", u"R_BRACK", u"BAR", u"L_VERT", u"R_VERT", + u"VERT", u"NORM", u"L_FLOOR", u"R_FLOOR", u"LL_CORNER", + u"LR_CORNER", u"L_CEIL", u"R_CEIL", u"UL_CORNER", u"UR_CORNER", + u"L_LEFT", u"R_RIGHT", u"ML_LEFT", u"MR_RIGHT", u"FUNC_LIM", + u"LIM_APPROACH_SYM", u"FUNC_INT", u"FUNC_SUM", u"FUNC_PROD", + u"FUNC_LOG", u"FUNC_LN", u"FUNC_EXP", u"FUNC_SIN", u"FUNC_COS", + u"FUNC_TAN", u"FUNC_CSC", u"FUNC_SEC", u"FUNC_COT", u"FUNC_ARCSIN", + u"FUNC_ARCCOS", u"FUNC_ARCTAN", u"FUNC_ARCCSC", u"FUNC_ARCSEC", + u"FUNC_ARCCOT", u"FUNC_SINH", u"FUNC_COSH", u"FUNC_TANH", + u"FUNC_ARSINH", u"FUNC_ARCOSH", u"FUNC_ARTANH", u"FUNC_ARCSINH", + u"FUNC_ARCCOSH", u"FUNC_ARCTANH", u"FUNC_ARSINH_NAME", + u"FUNC_ARCSINH_NAME", u"FUNC_ARCOSH_NAME", u"FUNC_ARCCOSH_NAME", + u"FUNC_ARTANH_NAME", u"FUNC_ARCTANH_NAME", u"FUNC_GCD_NAME", + u"FUNC_LCM_NAME", u"FUNC_FLOOR_NAME", u"FUNC_CEIL_NAME", + u"FUNC_SQRT", u"FUNC_GCD", u"FUNC_LCM", u"FUNC_FLOOR", + u"FUNC_CEIL", u"FUNC_MAX", u"FUNC_MIN", u"FUNC_DET", u"FUNC_EYE_NAME", + u"FUNC_ZEROS_NAME", u"FUNC_ONES_NAME", u"FUNC_COLS_NAME", + u"FUNC_ROWS_NAME", u"FUNC_DIAG_NAME", u"FUNC_NORM_NAME", + u"FUNC_RANK_NAME", u"FUNC_TRACE_NAME", u"FUNC_RREF_NAME", + u"FUNC_HSTACK_NAME", u"FUNC_VSTACK_NAME", u"FUNC_ORTHOGONALIZE_NAME", + u"FUNC_NULLSPACE_NAME", u"FUNC_DIAGONALIZE_NAME", u"FUNC_EIGENVALS_NAME", + u"FUNC_EIGENVECTORS_NAME", u"FUNC_SVD_NAME", u"CMD_TIMES", + u"CMD_CDOT", u"CMD_DIV", u"CMD_FRAC", u"CMD_BINOM", u"CMD_CHOOSE", + u"CMD_MOD", u"CMD_MATHIT", u"CMD_OPERATORNAME", u"MATRIX_TYPE_MATRIX", + u"MATRIX_TYPE_PMATRIX", u"MATRIX_TYPE_BMATRIX", u"MATRIX_TYPE_DET", + u"MATRIX_TYPES", u"CMD_MATRIX_START", u"CMD_MATRIX_END", + u"CMD_DET_START", u"CMD_DET_END", u"MATRIX_DEL_COL", u"MATRIX_DEL_ROW", + u"UNDERSCORE", u"CARET", u"COLON", u"SEMICOLON", u"COMMA", + u"PERIOD", u"WS_CHAR", u"DIFFERENTIAL", u"EXP_E", u"E_NOTATION_E", + u"LETTER_NO_E", u"LETTER", u"DIGIT", u"MATRIX_XRIGHTARROW", + u"TRANSFORM_EXCHANGE", u"NUMBER", u"E_NOTATION", u"IN", + u"ASSIGNMENT", u"EQUAL", u"LT", u"LTE", u"GT", u"GTE", + u"UNEQUAL", u"BANG", u"PERCENT_SIGN", u"PERCENT_NUMBER", + u"GREEK_LETTER", u"GREEK_CMD", u"OTHER_SYMBOL", u"OTHER_SYMBOL_CMD", + u"PI", u"INFTY_CMD", u"PARTIAL_CMD", u"INFTY", u"EMPTYSET", + u"SYMBOL", u"VARIABLE_CMD", u"VARIABLE_SYMBOL", u"VARIABLE"] + + grammarFileName = u"PS.g4" + + def __init__(self, input=None, output=sys.stdout): + super(PSLexer, self).__init__(input, output=output) + self.checkVersion("4.11.1") + self._interp = LexerATNSimulator(self, self.atn, self.decisionsToDFA, PredictionContextCache()) + self._actions = None + self._predicates = None diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.tokens b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.tokens new file mode 100755 index 0000000..d71163f --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSLexer.tokens @@ -0,0 +1,357 @@ +T__0=1 +T__1=2 +T__2=3 +T__3=4 +T__4=5 +T__5=6 +T__6=7 +T__7=8 +T__8=9 +T__9=10 +T__10=11 +T__11=12 +T__12=13 +T__13=14 +T__14=15 +T__15=16 +T__16=17 +T__17=18 +T__18=19 +T__19=20 +T__20=21 +T__21=22 +T__22=23 +T__23=24 +T__24=25 +T__25=26 +T__26=27 +T__27=28 +T__28=29 +T__29=30 +T__30=31 +T__31=32 +T__32=33 +T__33=34 +T__34=35 +T__35=36 +T__36=37 +T__37=38 +T__38=39 +T__39=40 +T__40=41 +T__41=42 +T__42=43 +T__43=44 +WS=45 +DOLLAR_SIGN=46 +ADD=47 +SUB=48 +MUL=49 +DIV=50 +L_PAREN=51 +R_PAREN=52 +L_GROUP=53 +R_GROUP=54 +L_BRACE=55 +R_BRACE=56 +L_BRACE_VISUAL=57 +R_BRACE_VISUAL=58 +L_BRACE_CMD=59 +R_BRACE_CMD=60 +L_BRACKET=61 +R_BRACKET=62 +L_BRACK=63 +R_BRACK=64 +BAR=65 +L_VERT=66 +R_VERT=67 +VERT=68 +NORM=69 +L_FLOOR=70 +R_FLOOR=71 +LL_CORNER=72 +LR_CORNER=73 +L_CEIL=74 +R_CEIL=75 +UL_CORNER=76 +UR_CORNER=77 +L_LEFT=78 +R_RIGHT=79 +ML_LEFT=80 +MR_RIGHT=81 +FUNC_LIM=82 +LIM_APPROACH_SYM=83 +FUNC_INT=84 +FUNC_SUM=85 +FUNC_PROD=86 +FUNC_LOG=87 +FUNC_LN=88 +FUNC_EXP=89 +FUNC_SIN=90 +FUNC_COS=91 +FUNC_TAN=92 +FUNC_CSC=93 +FUNC_SEC=94 +FUNC_COT=95 +FUNC_ARCSIN=96 +FUNC_ARCCOS=97 +FUNC_ARCTAN=98 +FUNC_ARCCSC=99 +FUNC_ARCSEC=100 +FUNC_ARCCOT=101 +FUNC_SINH=102 +FUNC_COSH=103 +FUNC_TANH=104 +FUNC_ARSINH=105 +FUNC_ARCOSH=106 +FUNC_ARTANH=107 +FUNC_ARCSINH=108 +FUNC_ARCCOSH=109 +FUNC_ARCTANH=110 +FUNC_ARSINH_NAME=111 +FUNC_ARCSINH_NAME=112 +FUNC_ARCOSH_NAME=113 +FUNC_ARCCOSH_NAME=114 +FUNC_ARTANH_NAME=115 +FUNC_ARCTANH_NAME=116 +FUNC_GCD_NAME=117 +FUNC_LCM_NAME=118 +FUNC_FLOOR_NAME=119 +FUNC_CEIL_NAME=120 +FUNC_SQRT=121 +FUNC_GCD=122 +FUNC_LCM=123 +FUNC_FLOOR=124 +FUNC_CEIL=125 +FUNC_MAX=126 +FUNC_MIN=127 +FUNC_DET=128 +FUNC_EYE_NAME=129 +FUNC_ZEROS_NAME=130 +FUNC_ONES_NAME=131 +FUNC_COLS_NAME=132 +FUNC_ROWS_NAME=133 +FUNC_DIAG_NAME=134 +FUNC_NORM_NAME=135 +FUNC_RANK_NAME=136 +FUNC_TRACE_NAME=137 +FUNC_RREF_NAME=138 +FUNC_HSTACK_NAME=139 +FUNC_VSTACK_NAME=140 +FUNC_ORTHOGONALIZE_NAME=141 +FUNC_NULLSPACE_NAME=142 +FUNC_DIAGONALIZE_NAME=143 +FUNC_EIGENVALS_NAME=144 +FUNC_EIGENVECTORS_NAME=145 +FUNC_SVD_NAME=146 +CMD_TIMES=147 +CMD_CDOT=148 +CMD_DIV=149 +CMD_FRAC=150 +CMD_BINOM=151 +CMD_CHOOSE=152 +CMD_MOD=153 +CMD_MATHIT=154 +CMD_OPERATORNAME=155 +MATRIX_TYPE_MATRIX=156 +MATRIX_TYPE_PMATRIX=157 +MATRIX_TYPE_BMATRIX=158 +MATRIX_TYPE_DET=159 +MATRIX_TYPES=160 +CMD_MATRIX_START=161 +CMD_MATRIX_END=162 +CMD_DET_START=163 +CMD_DET_END=164 +MATRIX_DEL_COL=165 +MATRIX_DEL_ROW=166 +UNDERSCORE=167 +CARET=168 +COLON=169 +SEMICOLON=170 +COMMA=171 +PERIOD=172 +DIFFERENTIAL=173 +EXP_E=174 +E_NOTATION_E=175 +LETTER_NO_E=176 +MATRIX_XRIGHTARROW=177 +TRANSFORM_EXCHANGE=178 +NUMBER=179 +E_NOTATION=180 +IN=181 +ASSIGNMENT=182 +EQUAL=183 +LT=184 +LTE=185 +GT=186 +GTE=187 +UNEQUAL=188 +BANG=189 +PERCENT_NUMBER=190 +GREEK_CMD=191 +OTHER_SYMBOL_CMD=192 +SYMBOL=193 +VARIABLE=194 +'\\acute'=1 +'\\bar'=2 +'\\overline'=3 +'\\breve'=4 +'\\check'=5 +'\\widecheck'=6 +'\\dot'=7 +'\\ddot'=8 +'\\grave'=9 +'\\hat'=10 +'\\tilde'=11 +'\\widetilde'=12 +'\\vec'=13 +'\\overrightarrow'=14 +'\\bm'=15 +'\\boldsymbol'=16 +'\\text'=17 +'\\textit'=18 +'\\mathbb'=19 +'\\mathbin'=20 +'\\mathbf'=21 +'\\mathcal'=22 +'\\mathclap'=23 +'\\mathclose'=24 +'\\mathellipsis'=25 +'\\mathfrak'=26 +'\\mathinner'=27 +'\\mathnormal'=28 +'\\mathop'=29 +'\\mathopen'=30 +'\\mathord'=31 +'\\mathpunct'=32 +'\\mathrel'=33 +'\\mathring'=34 +'\\mathrlap'=35 +'\\mathrm'=36 +'\\mathscr'=37 +'\\mathsf'=38 +'\\mathsterling'=39 +'\\mathtt'=40 +'^T'=41 +'^{T}'=42 +'^{\\top}'=43 +'\''=44 +'\\$'=46 +'+'=47 +'-'=48 +'*'=49 +'('=51 +')'=52 +'\\lgroup'=53 +'\\rgroup'=54 +'{'=55 +'}'=56 +'\\{'=57 +'\\}'=58 +'\\lbrace'=59 +'\\rbrace'=60 +'['=61 +']'=62 +'\\lbrack'=63 +'\\rbrack'=64 +'|'=65 +'\\lvert'=66 +'\\rvert'=67 +'\\vert'=68 +'\\|'=69 +'\\lfloor'=70 +'\\rfloor'=71 +'\\llcorner'=72 +'\\lrcorner'=73 +'\\lceil'=74 +'\\rceil'=75 +'\\ulcorner'=76 +'\\urcorner'=77 +'\\left'=78 +'\\right'=79 +'\\mleft'=80 +'\\mright'=81 +'\\lim'=82 +'\\int'=84 +'\\sum'=85 +'\\prod'=86 +'\\log'=87 +'\\ln'=88 +'\\exp'=89 +'\\sin'=90 +'\\cos'=91 +'\\tan'=92 +'\\csc'=93 +'\\sec'=94 +'\\cot'=95 +'\\arcsin'=96 +'\\arccos'=97 +'\\arctan'=98 +'\\arccsc'=99 +'\\arcsec'=100 +'\\arccot'=101 +'\\sinh'=102 +'\\cosh'=103 +'\\tanh'=104 +'\\arsinh'=105 +'\\arcosh'=106 +'\\artanh'=107 +'\\arcsinh'=108 +'\\arccosh'=109 +'\\arctanh'=110 +'arsinh'=111 +'arcsinh'=112 +'arcosh'=113 +'arccosh'=114 +'artanh'=115 +'arctanh'=116 +'gcd'=117 +'lcm'=118 +'floor'=119 +'ceil'=120 +'\\sqrt'=121 +'\\gcd'=122 +'\\lcm'=123 +'\\floor'=124 +'\\ceil'=125 +'\\max'=126 +'\\min'=127 +'\\det'=128 +'eye'=129 +'zeros'=130 +'ones'=131 +'cols'=132 +'rows'=133 +'diag'=134 +'norm'=135 +'rank'=136 +'rref'=138 +'hstack'=139 +'vstack'=140 +'nullspace'=142 +'\\times'=147 +'\\cdot'=148 +'\\div'=149 +'\\frac'=150 +'\\choose'=152 +'\\mod'=153 +'\\mathit'=154 +'\\operatorname'=155 +'matrix'=156 +'pmatrix'=157 +'bmatrix'=158 +'vmatrix'=159 +'&'=165 +'\\\\'=166 +'_'=167 +'^'=168 +':'=169 +';'=170 +','=171 +'.'=172 +'E'=175 +'\\in'=181 +'='=182 +'<'=184 +'>'=186 +'!'=189 diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSListener.py b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSListener.py new file mode 100755 index 0000000..0f7632c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSListener.py @@ -0,0 +1,573 @@ +# Generated from PS.g4 by ANTLR 4.11.1 +from antlr4 import * + +# This class defines a complete listener for a parse tree produced by PSParser. + + +class PSListener(ParseTreeListener): + + # Enter a parse tree produced by PSParser#accent_symbol. + def enterAccent_symbol(self, ctx): + pass + + # Exit a parse tree produced by PSParser#accent_symbol. + def exitAccent_symbol(self, ctx): + pass + + # Enter a parse tree produced by PSParser#math. + + def enterMath(self, ctx): + pass + + # Exit a parse tree produced by PSParser#math. + def exitMath(self, ctx): + pass + + # Enter a parse tree produced by PSParser#transpose. + + def enterTranspose(self, ctx): + pass + + # Exit a parse tree produced by PSParser#transpose. + def exitTranspose(self, ctx): + pass + + # Enter a parse tree produced by PSParser#transform_atom. + + def enterTransform_atom(self, ctx): + pass + + # Exit a parse tree produced by PSParser#transform_atom. + def exitTransform_atom(self, ctx): + pass + + # Enter a parse tree produced by PSParser#transform_scale. + + def enterTransform_scale(self, ctx): + pass + + # Exit a parse tree produced by PSParser#transform_scale. + def exitTransform_scale(self, ctx): + pass + + # Enter a parse tree produced by PSParser#transform_swap. + + def enterTransform_swap(self, ctx): + pass + + # Exit a parse tree produced by PSParser#transform_swap. + def exitTransform_swap(self, ctx): + pass + + # Enter a parse tree produced by PSParser#transform_assignment. + + def enterTransform_assignment(self, ctx): + pass + + # Exit a parse tree produced by PSParser#transform_assignment. + def exitTransform_assignment(self, ctx): + pass + + # Enter a parse tree produced by PSParser#elementary_transform. + + def enterElementary_transform(self, ctx): + pass + + # Exit a parse tree produced by PSParser#elementary_transform. + def exitElementary_transform(self, ctx): + pass + + # Enter a parse tree produced by PSParser#elementary_transforms. + + def enterElementary_transforms(self, ctx): + pass + + # Exit a parse tree produced by PSParser#elementary_transforms. + def exitElementary_transforms(self, ctx): + pass + + # Enter a parse tree produced by PSParser#matrix. + + def enterMatrix(self, ctx): + pass + + # Exit a parse tree produced by PSParser#matrix. + def exitMatrix(self, ctx): + pass + + # Enter a parse tree produced by PSParser#det. + + def enterDet(self, ctx): + pass + + # Exit a parse tree produced by PSParser#det. + def exitDet(self, ctx): + pass + + # Enter a parse tree produced by PSParser#matrix_row. + + def enterMatrix_row(self, ctx): + pass + + # Exit a parse tree produced by PSParser#matrix_row. + def exitMatrix_row(self, ctx): + pass + + # Enter a parse tree produced by PSParser#relation. + + def enterRelation(self, ctx): + pass + + # Exit a parse tree produced by PSParser#relation. + def exitRelation(self, ctx): + pass + + # Enter a parse tree produced by PSParser#relation_list. + + def enterRelation_list(self, ctx): + pass + + # Exit a parse tree produced by PSParser#relation_list. + def exitRelation_list(self, ctx): + pass + + # Enter a parse tree produced by PSParser#relation_list_content. + + def enterRelation_list_content(self, ctx): + pass + + # Exit a parse tree produced by PSParser#relation_list_content. + def exitRelation_list_content(self, ctx): + pass + + # Enter a parse tree produced by PSParser#equality. + + def enterEquality(self, ctx): + pass + + # Exit a parse tree produced by PSParser#equality. + def exitEquality(self, ctx): + pass + + # Enter a parse tree produced by PSParser#expr. + + def enterExpr(self, ctx): + pass + + # Exit a parse tree produced by PSParser#expr. + def exitExpr(self, ctx): + pass + + # Enter a parse tree produced by PSParser#additive. + + def enterAdditive(self, ctx): + pass + + # Exit a parse tree produced by PSParser#additive. + def exitAdditive(self, ctx): + pass + + # Enter a parse tree produced by PSParser#mp. + + def enterMp(self, ctx): + pass + + # Exit a parse tree produced by PSParser#mp. + def exitMp(self, ctx): + pass + + # Enter a parse tree produced by PSParser#mp_nofunc. + + def enterMp_nofunc(self, ctx): + pass + + # Exit a parse tree produced by PSParser#mp_nofunc. + def exitMp_nofunc(self, ctx): + pass + + # Enter a parse tree produced by PSParser#unary. + + def enterUnary(self, ctx): + pass + + # Exit a parse tree produced by PSParser#unary. + def exitUnary(self, ctx): + pass + + # Enter a parse tree produced by PSParser#unary_nofunc. + + def enterUnary_nofunc(self, ctx): + pass + + # Exit a parse tree produced by PSParser#unary_nofunc. + def exitUnary_nofunc(self, ctx): + pass + + # Enter a parse tree produced by PSParser#postfix. + + def enterPostfix(self, ctx): + pass + + # Exit a parse tree produced by PSParser#postfix. + def exitPostfix(self, ctx): + pass + + # Enter a parse tree produced by PSParser#postfix_nofunc. + + def enterPostfix_nofunc(self, ctx): + pass + + # Exit a parse tree produced by PSParser#postfix_nofunc. + def exitPostfix_nofunc(self, ctx): + pass + + # Enter a parse tree produced by PSParser#postfix_op. + + def enterPostfix_op(self, ctx): + pass + + # Exit a parse tree produced by PSParser#postfix_op. + def exitPostfix_op(self, ctx): + pass + + # Enter a parse tree produced by PSParser#eval_at. + + def enterEval_at(self, ctx): + pass + + # Exit a parse tree produced by PSParser#eval_at. + def exitEval_at(self, ctx): + pass + + # Enter a parse tree produced by PSParser#eval_at_sub. + + def enterEval_at_sub(self, ctx): + pass + + # Exit a parse tree produced by PSParser#eval_at_sub. + def exitEval_at_sub(self, ctx): + pass + + # Enter a parse tree produced by PSParser#eval_at_sup. + + def enterEval_at_sup(self, ctx): + pass + + # Exit a parse tree produced by PSParser#eval_at_sup. + def exitEval_at_sup(self, ctx): + pass + + # Enter a parse tree produced by PSParser#exp. + + def enterExp(self, ctx): + pass + + # Exit a parse tree produced by PSParser#exp. + def exitExp(self, ctx): + pass + + # Enter a parse tree produced by PSParser#exp_nofunc. + + def enterExp_nofunc(self, ctx): + pass + + # Exit a parse tree produced by PSParser#exp_nofunc. + def exitExp_nofunc(self, ctx): + pass + + # Enter a parse tree produced by PSParser#comp. + + def enterComp(self, ctx): + pass + + # Exit a parse tree produced by PSParser#comp. + def exitComp(self, ctx): + pass + + # Enter a parse tree produced by PSParser#comp_nofunc. + + def enterComp_nofunc(self, ctx): + pass + + # Exit a parse tree produced by PSParser#comp_nofunc. + def exitComp_nofunc(self, ctx): + pass + + # Enter a parse tree produced by PSParser#group. + + def enterGroup(self, ctx): + pass + + # Exit a parse tree produced by PSParser#group. + def exitGroup(self, ctx): + pass + + # Enter a parse tree produced by PSParser#norm_group. + + def enterNorm_group(self, ctx): + pass + + # Exit a parse tree produced by PSParser#norm_group. + def exitNorm_group(self, ctx): + pass + + # Enter a parse tree produced by PSParser#abs_group. + + def enterAbs_group(self, ctx): + pass + + # Exit a parse tree produced by PSParser#abs_group. + def exitAbs_group(self, ctx): + pass + + # Enter a parse tree produced by PSParser#floor_group. + + def enterFloor_group(self, ctx): + pass + + # Exit a parse tree produced by PSParser#floor_group. + def exitFloor_group(self, ctx): + pass + + # Enter a parse tree produced by PSParser#ceil_group. + + def enterCeil_group(self, ctx): + pass + + # Exit a parse tree produced by PSParser#ceil_group. + def exitCeil_group(self, ctx): + pass + + # Enter a parse tree produced by PSParser#accent. + + def enterAccent(self, ctx): + pass + + # Exit a parse tree produced by PSParser#accent. + def exitAccent(self, ctx): + pass + + # Enter a parse tree produced by PSParser#atom_expr_no_supexpr. + + def enterAtom_expr_no_supexpr(self, ctx): + pass + + # Exit a parse tree produced by PSParser#atom_expr_no_supexpr. + def exitAtom_expr_no_supexpr(self, ctx): + pass + + # Enter a parse tree produced by PSParser#atom_expr. + + def enterAtom_expr(self, ctx): + pass + + # Exit a parse tree produced by PSParser#atom_expr. + def exitAtom_expr(self, ctx): + pass + + # Enter a parse tree produced by PSParser#atom. + + def enterAtom(self, ctx): + pass + + # Exit a parse tree produced by PSParser#atom. + def exitAtom(self, ctx): + pass + + # Enter a parse tree produced by PSParser#mathit. + + def enterMathit(self, ctx): + pass + + # Exit a parse tree produced by PSParser#mathit. + def exitMathit(self, ctx): + pass + + # Enter a parse tree produced by PSParser#mathit_text. + + def enterMathit_text(self, ctx): + pass + + # Exit a parse tree produced by PSParser#mathit_text. + def exitMathit_text(self, ctx): + pass + + # Enter a parse tree produced by PSParser#frac. + + def enterFrac(self, ctx): + pass + + # Exit a parse tree produced by PSParser#frac. + def exitFrac(self, ctx): + pass + + # Enter a parse tree produced by PSParser#binom. + + def enterBinom(self, ctx): + pass + + # Exit a parse tree produced by PSParser#binom. + def exitBinom(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_normal_functions_single_arg. + + def enterFunc_normal_functions_single_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_normal_functions_single_arg. + def exitFunc_normal_functions_single_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_normal_functions_multi_arg. + + def enterFunc_normal_functions_multi_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_normal_functions_multi_arg. + def exitFunc_normal_functions_multi_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_operator_names_single_arg. + + def enterFunc_operator_names_single_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_operator_names_single_arg. + def exitFunc_operator_names_single_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_operator_names_multi_arg. + + def enterFunc_operator_names_multi_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_operator_names_multi_arg. + def exitFunc_operator_names_multi_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_normal_single_arg. + + def enterFunc_normal_single_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_normal_single_arg. + def exitFunc_normal_single_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_normal_multi_arg. + + def enterFunc_normal_multi_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_normal_multi_arg. + def exitFunc_normal_multi_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func. + + def enterFunc(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func. + def exitFunc(self, ctx): + pass + + # Enter a parse tree produced by PSParser#args. + + def enterArgs(self, ctx): + pass + + # Exit a parse tree produced by PSParser#args. + def exitArgs(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_common_args. + + def enterFunc_common_args(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_common_args. + def exitFunc_common_args(self, ctx): + pass + + # Enter a parse tree produced by PSParser#limit_sub. + + def enterLimit_sub(self, ctx): + pass + + # Exit a parse tree produced by PSParser#limit_sub. + def exitLimit_sub(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_single_arg. + + def enterFunc_single_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_single_arg. + def exitFunc_single_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_single_arg_noparens. + + def enterFunc_single_arg_noparens(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_single_arg_noparens. + def exitFunc_single_arg_noparens(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_multi_arg. + + def enterFunc_multi_arg(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_multi_arg. + def exitFunc_multi_arg(self, ctx): + pass + + # Enter a parse tree produced by PSParser#func_multi_arg_noparens. + + def enterFunc_multi_arg_noparens(self, ctx): + pass + + # Exit a parse tree produced by PSParser#func_multi_arg_noparens. + def exitFunc_multi_arg_noparens(self, ctx): + pass + + # Enter a parse tree produced by PSParser#subexpr. + + def enterSubexpr(self, ctx): + pass + + # Exit a parse tree produced by PSParser#subexpr. + def exitSubexpr(self, ctx): + pass + + # Enter a parse tree produced by PSParser#supexpr. + + def enterSupexpr(self, ctx): + pass + + # Exit a parse tree produced by PSParser#supexpr. + def exitSupexpr(self, ctx): + pass + + # Enter a parse tree produced by PSParser#subeq. + + def enterSubeq(self, ctx): + pass + + # Exit a parse tree produced by PSParser#subeq. + def exitSubeq(self, ctx): + pass + + # Enter a parse tree produced by PSParser#supeq. + + def enterSupeq(self, ctx): + pass + + # Exit a parse tree produced by PSParser#supeq. + def exitSupeq(self, ctx): + pass diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSParser.py b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSParser.py new file mode 100755 index 0000000..b651b50 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/PSParser.py @@ -0,0 +1,6486 @@ +# Generated from PS.g4 by ANTLR 4.11.1 +# encoding: utf-8 +from __future__ import print_function +from antlr4 import * +from io import StringIO +import sys + + +def serializedATN(): + return [ + 4, 1, 194, 1046, 2, 0, 7, 0, 2, 1, 7, 1, 2, 2, 7, 2, 2, 3, 7, 3, 2, 4, 7, 4, 2, 5, 7, 5, 2, 6, + 7, 6, 2, 7, 7, 7, 2, 8, 7, 8, 2, 9, 7, 9, 2, 10, 7, 10, 2, 11, 7, 11, 2, 12, 7, 12, 2, 13, 7, + 13, 2, 14, 7, 14, 2, 15, 7, 15, 2, 16, 7, 16, 2, 17, 7, 17, 2, 18, 7, 18, 2, 19, 7, 19, 2, + 20, 7, 20, 2, 21, 7, 21, 2, 22, 7, 22, 2, 23, 7, 23, 2, 24, 7, 24, 2, 25, 7, 25, 2, 26, 7, + 26, 2, 27, 7, 27, 2, 28, 7, 28, 2, 29, 7, 29, 2, 30, 7, 30, 2, 31, 7, 31, 2, 32, 7, 32, 2, + 33, 7, 33, 2, 34, 7, 34, 2, 35, 7, 35, 2, 36, 7, 36, 2, 37, 7, 37, 2, 38, 7, 38, 2, 39, 7, + 39, 2, 40, 7, 40, 2, 41, 7, 41, 2, 42, 7, 42, 2, 43, 7, 43, 2, 44, 7, 44, 2, 45, 7, 45, 2, + 46, 7, 46, 2, 47, 7, 47, 2, 48, 7, 48, 2, 49, 7, 49, 2, 50, 7, 50, 2, 51, 7, 51, 2, 52, 7, + 52, 2, 53, 7, 53, 2, 54, 7, 54, 2, 55, 7, 55, 2, 56, 7, 56, 2, 57, 7, 57, 2, 58, 7, 58, 2, + 59, 7, 59, 2, 60, 7, 60, 2, 61, 7, 61, 2, 62, 7, 62, 1, 0, 1, 0, 1, 1, 1, 1, 3, 1, 131, 8, + 1, 1, 2, 1, 2, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 3, 3, 141, 8, 3, 1, 4, 1, 4, 1, 4, 1, 4, 3, + 4, 147, 8, 4, 1, 4, 1, 4, 1, 5, 1, 5, 1, 5, 1, 5, 1, 6, 1, 6, 1, 6, 1, 7, 1, 7, 1, 7, 3, 7, 161, + 8, 7, 1, 8, 1, 8, 1, 8, 5, 8, 166, 8, 8, 10, 8, 12, 8, 169, 9, 8, 1, 9, 1, 9, 1, 9, 1, 9, 5, + 9, 175, 8, 9, 10, 9, 12, 9, 178, 9, 9, 1, 9, 3, 9, 181, 8, 9, 1, 9, 1, 9, 1, 9, 1, 9, 1, 9, + 1, 9, 3, 9, 189, 8, 9, 1, 9, 1, 9, 1, 9, 1, 9, 3, 9, 195, 8, 9, 1, 10, 1, 10, 1, 10, 1, 10, + 5, 10, 201, 8, 10, 10, 10, 12, 10, 204, 9, 10, 1, 10, 3, 10, 207, 8, 10, 1, 10, 1, 10, + 1, 11, 1, 11, 1, 11, 5, 11, 214, 8, 11, 10, 11, 12, 11, 217, 9, 11, 1, 12, 1, 12, 1, 12, + 1, 12, 1, 12, 1, 12, 5, 12, 225, 8, 12, 10, 12, 12, 12, 228, 9, 12, 1, 13, 1, 13, 1, 13, + 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, + 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, + 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 1, 13, 3, 13, 267, 8, 13, 1, 14, 1, 14, + 1, 14, 1, 14, 1, 14, 5, 14, 274, 8, 14, 10, 14, 12, 14, 277, 9, 14, 1, 14, 1, 14, 1, 14, + 1, 14, 1, 14, 5, 14, 284, 8, 14, 10, 14, 12, 14, 287, 9, 14, 3, 14, 289, 8, 14, 1, 15, + 1, 15, 1, 15, 1, 15, 1, 16, 1, 16, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 1, 17, 5, 17, 303, + 8, 17, 10, 17, 12, 17, 306, 9, 17, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 1, 18, 5, 18, 314, + 8, 18, 10, 18, 12, 18, 317, 9, 18, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 1, 19, 5, 19, 325, + 8, 19, 10, 19, 12, 19, 328, 9, 19, 1, 20, 1, 20, 1, 20, 4, 20, 333, 8, 20, 11, 20, 12, + 20, 334, 3, 20, 337, 8, 20, 1, 21, 1, 21, 1, 21, 1, 21, 5, 21, 343, 8, 21, 10, 21, 12, + 21, 346, 9, 21, 3, 21, 348, 8, 21, 1, 22, 1, 22, 5, 22, 352, 8, 22, 10, 22, 12, 22, 355, + 9, 22, 1, 23, 1, 23, 5, 23, 359, 8, 23, 10, 23, 12, 23, 362, 9, 23, 1, 24, 1, 24, 1, 24, + 3, 24, 367, 8, 24, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 1, 25, 3, 25, 375, 8, 25, 1, 26, 1, + 26, 1, 26, 1, 26, 3, 26, 381, 8, 26, 1, 26, 1, 26, 1, 27, 1, 27, 1, 27, 1, 27, 3, 27, 389, + 8, 27, 1, 27, 1, 27, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, 1, 28, + 3, 28, 403, 8, 28, 1, 28, 3, 28, 406, 8, 28, 5, 28, 408, 8, 28, 10, 28, 12, 28, 411, 9, + 28, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 1, 29, 3, 29, 423, 8, + 29, 1, 29, 3, 29, 426, 8, 29, 5, 29, 428, 8, 29, 10, 29, 12, 29, 431, 9, 29, 1, 30, 1, + 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 1, 30, 3, 30, 444, 8, 30, 1, + 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 1, 31, 3, 31, 456, 8, 31, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, + 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 1, 32, 3, 32, 570, 8, 32, 1, 33, 1, 33, 1, + 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, 33, 1, + 33, 3, 33, 588, 8, 33, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, + 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, + 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, + 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 1, 34, 3, + 34, 638, 8, 34, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, + 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, + 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 1, 35, 3, 35, 672, 8, 35, 1, 36, 1, + 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, + 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, 36, 1, + 36, 1, 36, 1, 36, 1, 36, 1, 36, 3, 36, 706, 8, 36, 1, 37, 1, 37, 1, 37, 1, 37, 1, 37, 1, + 38, 1, 38, 1, 38, 1, 38, 3, 38, 717, 8, 38, 1, 38, 3, 38, 720, 8, 38, 1, 39, 1, 39, 1, 39, + 1, 39, 3, 39, 726, 8, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 1, 39, 3, 39, + 736, 8, 39, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 1, 40, 3, 40, 746, 8, 40, 1, + 41, 1, 41, 1, 41, 1, 41, 1, 41, 1, 42, 4, 42, 754, 8, 42, 11, 42, 12, 42, 755, 1, 43, 1, + 43, 1, 43, 1, 43, 1, 43, 1, 43, 1, 43, 1, 43, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, + 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 1, 44, 3, 44, 780, 8, 44, 1, 45, 1, 45, 1, + 46, 1, 46, 1, 47, 1, 47, 1, 48, 1, 48, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 1, 49, 3, 49, 796, + 8, 49, 1, 50, 1, 50, 1, 50, 1, 50, 1, 50, 1, 50, 3, 50, 804, 8, 50, 1, 51, 1, 51, 3, 51, + 808, 8, 51, 1, 51, 3, 51, 811, 8, 51, 1, 51, 3, 51, 814, 8, 51, 1, 51, 3, 51, 817, 8, 51, + 3, 51, 819, 8, 51, 1, 51, 3, 51, 822, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 827, 8, 51, 1, + 51, 1, 51, 1, 51, 3, 51, 832, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 837, 8, 51, 1, 51, 1, 51, + 1, 51, 3, 51, 842, 8, 51, 1, 51, 1, 51, 3, 51, 846, 8, 51, 1, 51, 3, 51, 849, 8, 51, 1, + 51, 3, 51, 852, 8, 51, 1, 51, 3, 51, 855, 8, 51, 3, 51, 857, 8, 51, 1, 51, 3, 51, 860, + 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 865, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 870, 8, 51, 1, + 51, 1, 51, 1, 51, 3, 51, 875, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 880, 8, 51, 1, 51, 1, 51, + 3, 51, 884, 8, 51, 1, 51, 3, 51, 887, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 893, 8, + 51, 1, 51, 1, 51, 3, 51, 897, 8, 51, 1, 51, 1, 51, 3, 51, 901, 8, 51, 1, 51, 1, 51, 1, 51, + 1, 51, 3, 51, 907, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, + 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, + 1, 51, 3, 51, 932, 8, 51, 1, 51, 3, 51, 935, 8, 51, 1, 51, 1, 51, 1, 51, 3, 51, 940, 8, + 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 947, 8, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, + 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 960, 8, 51, 1, 51, 1, 51, 1, 51, 1, + 51, 1, 51, 1, 51, 1, 51, 1, 51, 3, 51, 970, 8, 51, 3, 51, 972, 8, 51, 1, 52, 1, 52, 1, 52, + 1, 52, 1, 52, 3, 52, 979, 8, 52, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, 1, 53, + 3, 53, 989, 8, 53, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 1, 54, 3, 54, + 1000, 8, 54, 1, 54, 1, 54, 1, 55, 1, 55, 1, 56, 1, 56, 1, 57, 1, 57, 1, 57, 1, 57, 1, 57, + 3, 57, 1013, 8, 57, 1, 58, 1, 58, 1, 59, 1, 59, 1, 59, 1, 59, 1, 59, 3, 59, 1022, 8, 59, + 1, 59, 1, 59, 3, 59, 1026, 8, 59, 1, 60, 1, 60, 1, 60, 1, 60, 1, 60, 1, 60, 3, 60, 1034, + 8, 60, 1, 61, 1, 61, 1, 61, 1, 61, 1, 61, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 1, 62, 0, 6, + 24, 34, 36, 38, 56, 58, 63, 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, + 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, + 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, + 114, 116, 118, 120, 122, 124, 0, 15, 2, 0, 1, 40, 154, 154, 1, 0, 41, 44, 1, 0, 181, + 188, 1, 0, 182, 183, 1, 0, 47, 48, 4, 0, 49, 50, 147, 149, 153, 153, 169, 169, 1, 0, + 174, 176, 3, 0, 87, 110, 124, 125, 128, 128, 2, 0, 122, 123, 126, 127, 6, 0, 111, 116, + 119, 120, 129, 129, 132, 133, 135, 138, 142, 146, 4, 0, 117, 118, 130, 131, 134, + 134, 139, 141, 2, 0, 51, 51, 61, 61, 2, 0, 52, 52, 62, 62, 1, 0, 85, 86, 2, 0, 176, 176, + 191, 192, 1164, 0, 126, 1, 0, 0, 0, 2, 130, 1, 0, 0, 0, 4, 132, 1, 0, 0, 0, 6, 134, 1, 0, + 0, 0, 8, 146, 1, 0, 0, 0, 10, 150, 1, 0, 0, 0, 12, 154, 1, 0, 0, 0, 14, 160, 1, 0, 0, 0, 16, + 162, 1, 0, 0, 0, 18, 170, 1, 0, 0, 0, 20, 196, 1, 0, 0, 0, 22, 210, 1, 0, 0, 0, 24, 218, + 1, 0, 0, 0, 26, 266, 1, 0, 0, 0, 28, 288, 1, 0, 0, 0, 30, 290, 1, 0, 0, 0, 32, 294, 1, 0, + 0, 0, 34, 296, 1, 0, 0, 0, 36, 307, 1, 0, 0, 0, 38, 318, 1, 0, 0, 0, 40, 336, 1, 0, 0, 0, + 42, 347, 1, 0, 0, 0, 44, 349, 1, 0, 0, 0, 46, 356, 1, 0, 0, 0, 48, 366, 1, 0, 0, 0, 50, 368, + 1, 0, 0, 0, 52, 376, 1, 0, 0, 0, 54, 384, 1, 0, 0, 0, 56, 392, 1, 0, 0, 0, 58, 412, 1, 0, + 0, 0, 60, 443, 1, 0, 0, 0, 62, 455, 1, 0, 0, 0, 64, 569, 1, 0, 0, 0, 66, 587, 1, 0, 0, 0, + 68, 637, 1, 0, 0, 0, 70, 671, 1, 0, 0, 0, 72, 705, 1, 0, 0, 0, 74, 707, 1, 0, 0, 0, 76, 716, + 1, 0, 0, 0, 78, 725, 1, 0, 0, 0, 80, 745, 1, 0, 0, 0, 82, 747, 1, 0, 0, 0, 84, 753, 1, 0, + 0, 0, 86, 757, 1, 0, 0, 0, 88, 779, 1, 0, 0, 0, 90, 781, 1, 0, 0, 0, 92, 783, 1, 0, 0, 0, + 94, 785, 1, 0, 0, 0, 96, 787, 1, 0, 0, 0, 98, 795, 1, 0, 0, 0, 100, 803, 1, 0, 0, 0, 102, + 971, 1, 0, 0, 0, 104, 978, 1, 0, 0, 0, 106, 988, 1, 0, 0, 0, 108, 990, 1, 0, 0, 0, 110, + 1003, 1, 0, 0, 0, 112, 1005, 1, 0, 0, 0, 114, 1012, 1, 0, 0, 0, 116, 1014, 1, 0, 0, 0, + 118, 1016, 1, 0, 0, 0, 120, 1027, 1, 0, 0, 0, 122, 1035, 1, 0, 0, 0, 124, 1040, 1, 0, + 0, 0, 126, 127, 7, 0, 0, 0, 127, 1, 1, 0, 0, 0, 128, 131, 3, 24, 12, 0, 129, 131, 3, 26, + 13, 0, 130, 128, 1, 0, 0, 0, 130, 129, 1, 0, 0, 0, 131, 3, 1, 0, 0, 0, 132, 133, 7, 1, 0, + 0, 133, 5, 1, 0, 0, 0, 134, 135, 5, 176, 0, 0, 135, 140, 5, 167, 0, 0, 136, 141, 5, 179, + 0, 0, 137, 138, 5, 55, 0, 0, 138, 139, 5, 179, 0, 0, 139, 141, 5, 56, 0, 0, 140, 136, + 1, 0, 0, 0, 140, 137, 1, 0, 0, 0, 141, 7, 1, 0, 0, 0, 142, 147, 3, 32, 16, 0, 143, 147, + 3, 64, 32, 0, 144, 147, 5, 47, 0, 0, 145, 147, 5, 48, 0, 0, 146, 142, 1, 0, 0, 0, 146, + 143, 1, 0, 0, 0, 146, 144, 1, 0, 0, 0, 146, 145, 1, 0, 0, 0, 147, 148, 1, 0, 0, 0, 148, + 149, 3, 6, 3, 0, 149, 9, 1, 0, 0, 0, 150, 151, 3, 6, 3, 0, 151, 152, 5, 178, 0, 0, 152, + 153, 3, 6, 3, 0, 153, 11, 1, 0, 0, 0, 154, 155, 3, 6, 3, 0, 155, 156, 3, 8, 4, 0, 156, 13, + 1, 0, 0, 0, 157, 161, 3, 12, 6, 0, 158, 161, 3, 8, 4, 0, 159, 161, 3, 10, 5, 0, 160, 157, + 1, 0, 0, 0, 160, 158, 1, 0, 0, 0, 160, 159, 1, 0, 0, 0, 161, 15, 1, 0, 0, 0, 162, 167, 3, + 14, 7, 0, 163, 164, 5, 171, 0, 0, 164, 166, 3, 14, 7, 0, 165, 163, 1, 0, 0, 0, 166, 169, + 1, 0, 0, 0, 167, 165, 1, 0, 0, 0, 167, 168, 1, 0, 0, 0, 168, 17, 1, 0, 0, 0, 169, 167, 1, + 0, 0, 0, 170, 171, 5, 161, 0, 0, 171, 176, 3, 22, 11, 0, 172, 173, 5, 166, 0, 0, 173, + 175, 3, 22, 11, 0, 174, 172, 1, 0, 0, 0, 175, 178, 1, 0, 0, 0, 176, 174, 1, 0, 0, 0, 176, + 177, 1, 0, 0, 0, 177, 180, 1, 0, 0, 0, 178, 176, 1, 0, 0, 0, 179, 181, 5, 166, 0, 0, 180, + 179, 1, 0, 0, 0, 180, 181, 1, 0, 0, 0, 181, 182, 1, 0, 0, 0, 182, 194, 5, 162, 0, 0, 183, + 188, 5, 177, 0, 0, 184, 185, 5, 61, 0, 0, 185, 186, 3, 16, 8, 0, 186, 187, 5, 62, 0, 0, + 187, 189, 1, 0, 0, 0, 188, 184, 1, 0, 0, 0, 188, 189, 1, 0, 0, 0, 189, 190, 1, 0, 0, 0, + 190, 191, 5, 55, 0, 0, 191, 192, 3, 16, 8, 0, 192, 193, 5, 56, 0, 0, 193, 195, 1, 0, 0, + 0, 194, 183, 1, 0, 0, 0, 194, 195, 1, 0, 0, 0, 195, 19, 1, 0, 0, 0, 196, 197, 5, 163, 0, + 0, 197, 202, 3, 22, 11, 0, 198, 199, 5, 166, 0, 0, 199, 201, 3, 22, 11, 0, 200, 198, + 1, 0, 0, 0, 201, 204, 1, 0, 0, 0, 202, 200, 1, 0, 0, 0, 202, 203, 1, 0, 0, 0, 203, 206, + 1, 0, 0, 0, 204, 202, 1, 0, 0, 0, 205, 207, 5, 166, 0, 0, 206, 205, 1, 0, 0, 0, 206, 207, + 1, 0, 0, 0, 207, 208, 1, 0, 0, 0, 208, 209, 5, 164, 0, 0, 209, 21, 1, 0, 0, 0, 210, 215, + 3, 32, 16, 0, 211, 212, 5, 165, 0, 0, 212, 214, 3, 32, 16, 0, 213, 211, 1, 0, 0, 0, 214, + 217, 1, 0, 0, 0, 215, 213, 1, 0, 0, 0, 215, 216, 1, 0, 0, 0, 216, 23, 1, 0, 0, 0, 217, 215, + 1, 0, 0, 0, 218, 219, 6, 12, -1, 0, 219, 220, 3, 32, 16, 0, 220, 226, 1, 0, 0, 0, 221, + 222, 10, 2, 0, 0, 222, 223, 7, 2, 0, 0, 223, 225, 3, 24, 12, 3, 224, 221, 1, 0, 0, 0, 225, + 228, 1, 0, 0, 0, 226, 224, 1, 0, 0, 0, 226, 227, 1, 0, 0, 0, 227, 25, 1, 0, 0, 0, 228, 226, + 1, 0, 0, 0, 229, 267, 3, 28, 14, 0, 230, 231, 5, 61, 0, 0, 231, 232, 3, 28, 14, 0, 232, + 233, 5, 62, 0, 0, 233, 267, 1, 0, 0, 0, 234, 235, 5, 55, 0, 0, 235, 236, 3, 28, 14, 0, + 236, 237, 5, 56, 0, 0, 237, 267, 1, 0, 0, 0, 238, 239, 5, 57, 0, 0, 239, 240, 3, 28, 14, + 0, 240, 241, 5, 58, 0, 0, 241, 267, 1, 0, 0, 0, 242, 243, 5, 78, 0, 0, 243, 244, 5, 61, + 0, 0, 244, 245, 3, 28, 14, 0, 245, 246, 5, 79, 0, 0, 246, 247, 5, 62, 0, 0, 247, 267, + 1, 0, 0, 0, 248, 249, 5, 78, 0, 0, 249, 250, 5, 57, 0, 0, 250, 251, 3, 28, 14, 0, 251, + 252, 5, 79, 0, 0, 252, 253, 5, 58, 0, 0, 253, 267, 1, 0, 0, 0, 254, 255, 5, 80, 0, 0, 255, + 256, 5, 61, 0, 0, 256, 257, 3, 28, 14, 0, 257, 258, 5, 81, 0, 0, 258, 259, 5, 62, 0, 0, + 259, 267, 1, 0, 0, 0, 260, 261, 5, 80, 0, 0, 261, 262, 5, 57, 0, 0, 262, 263, 3, 28, 14, + 0, 263, 264, 5, 81, 0, 0, 264, 265, 5, 58, 0, 0, 265, 267, 1, 0, 0, 0, 266, 229, 1, 0, + 0, 0, 266, 230, 1, 0, 0, 0, 266, 234, 1, 0, 0, 0, 266, 238, 1, 0, 0, 0, 266, 242, 1, 0, + 0, 0, 266, 248, 1, 0, 0, 0, 266, 254, 1, 0, 0, 0, 266, 260, 1, 0, 0, 0, 267, 27, 1, 0, 0, + 0, 268, 269, 3, 24, 12, 0, 269, 270, 5, 171, 0, 0, 270, 275, 3, 24, 12, 0, 271, 272, + 5, 171, 0, 0, 272, 274, 3, 24, 12, 0, 273, 271, 1, 0, 0, 0, 274, 277, 1, 0, 0, 0, 275, + 273, 1, 0, 0, 0, 275, 276, 1, 0, 0, 0, 276, 289, 1, 0, 0, 0, 277, 275, 1, 0, 0, 0, 278, + 279, 3, 24, 12, 0, 279, 280, 5, 170, 0, 0, 280, 285, 3, 24, 12, 0, 281, 282, 5, 170, + 0, 0, 282, 284, 3, 24, 12, 0, 283, 281, 1, 0, 0, 0, 284, 287, 1, 0, 0, 0, 285, 283, 1, + 0, 0, 0, 285, 286, 1, 0, 0, 0, 286, 289, 1, 0, 0, 0, 287, 285, 1, 0, 0, 0, 288, 268, 1, + 0, 0, 0, 288, 278, 1, 0, 0, 0, 289, 29, 1, 0, 0, 0, 290, 291, 3, 32, 16, 0, 291, 292, 7, + 3, 0, 0, 292, 293, 3, 32, 16, 0, 293, 31, 1, 0, 0, 0, 294, 295, 3, 34, 17, 0, 295, 33, + 1, 0, 0, 0, 296, 297, 6, 17, -1, 0, 297, 298, 3, 36, 18, 0, 298, 304, 1, 0, 0, 0, 299, + 300, 10, 2, 0, 0, 300, 301, 7, 4, 0, 0, 301, 303, 3, 34, 17, 3, 302, 299, 1, 0, 0, 0, 303, + 306, 1, 0, 0, 0, 304, 302, 1, 0, 0, 0, 304, 305, 1, 0, 0, 0, 305, 35, 1, 0, 0, 0, 306, 304, + 1, 0, 0, 0, 307, 308, 6, 18, -1, 0, 308, 309, 3, 40, 20, 0, 309, 315, 1, 0, 0, 0, 310, + 311, 10, 2, 0, 0, 311, 312, 7, 5, 0, 0, 312, 314, 3, 36, 18, 3, 313, 310, 1, 0, 0, 0, 314, + 317, 1, 0, 0, 0, 315, 313, 1, 0, 0, 0, 315, 316, 1, 0, 0, 0, 316, 37, 1, 0, 0, 0, 317, 315, + 1, 0, 0, 0, 318, 319, 6, 19, -1, 0, 319, 320, 3, 42, 21, 0, 320, 326, 1, 0, 0, 0, 321, + 322, 10, 2, 0, 0, 322, 323, 7, 5, 0, 0, 323, 325, 3, 38, 19, 3, 324, 321, 1, 0, 0, 0, 325, + 328, 1, 0, 0, 0, 326, 324, 1, 0, 0, 0, 326, 327, 1, 0, 0, 0, 327, 39, 1, 0, 0, 0, 328, 326, + 1, 0, 0, 0, 329, 330, 7, 4, 0, 0, 330, 337, 3, 40, 20, 0, 331, 333, 3, 44, 22, 0, 332, + 331, 1, 0, 0, 0, 333, 334, 1, 0, 0, 0, 334, 332, 1, 0, 0, 0, 334, 335, 1, 0, 0, 0, 335, + 337, 1, 0, 0, 0, 336, 329, 1, 0, 0, 0, 336, 332, 1, 0, 0, 0, 337, 41, 1, 0, 0, 0, 338, 339, + 7, 4, 0, 0, 339, 348, 3, 42, 21, 0, 340, 344, 3, 44, 22, 0, 341, 343, 3, 46, 23, 0, 342, + 341, 1, 0, 0, 0, 343, 346, 1, 0, 0, 0, 344, 342, 1, 0, 0, 0, 344, 345, 1, 0, 0, 0, 345, + 348, 1, 0, 0, 0, 346, 344, 1, 0, 0, 0, 347, 338, 1, 0, 0, 0, 347, 340, 1, 0, 0, 0, 348, + 43, 1, 0, 0, 0, 349, 353, 3, 56, 28, 0, 350, 352, 3, 48, 24, 0, 351, 350, 1, 0, 0, 0, 352, + 355, 1, 0, 0, 0, 353, 351, 1, 0, 0, 0, 353, 354, 1, 0, 0, 0, 354, 45, 1, 0, 0, 0, 355, 353, + 1, 0, 0, 0, 356, 360, 3, 58, 29, 0, 357, 359, 3, 48, 24, 0, 358, 357, 1, 0, 0, 0, 359, + 362, 1, 0, 0, 0, 360, 358, 1, 0, 0, 0, 360, 361, 1, 0, 0, 0, 361, 47, 1, 0, 0, 0, 362, 360, + 1, 0, 0, 0, 363, 367, 5, 189, 0, 0, 364, 367, 3, 50, 25, 0, 365, 367, 3, 4, 2, 0, 366, + 363, 1, 0, 0, 0, 366, 364, 1, 0, 0, 0, 366, 365, 1, 0, 0, 0, 367, 49, 1, 0, 0, 0, 368, 374, + 5, 65, 0, 0, 369, 375, 3, 54, 27, 0, 370, 375, 3, 52, 26, 0, 371, 372, 3, 54, 27, 0, 372, + 373, 3, 52, 26, 0, 373, 375, 1, 0, 0, 0, 374, 369, 1, 0, 0, 0, 374, 370, 1, 0, 0, 0, 374, + 371, 1, 0, 0, 0, 375, 51, 1, 0, 0, 0, 376, 377, 5, 167, 0, 0, 377, 380, 5, 55, 0, 0, 378, + 381, 3, 32, 16, 0, 379, 381, 3, 30, 15, 0, 380, 378, 1, 0, 0, 0, 380, 379, 1, 0, 0, 0, + 381, 382, 1, 0, 0, 0, 382, 383, 5, 56, 0, 0, 383, 53, 1, 0, 0, 0, 384, 385, 5, 168, 0, + 0, 385, 388, 5, 55, 0, 0, 386, 389, 3, 32, 16, 0, 387, 389, 3, 30, 15, 0, 388, 386, 1, + 0, 0, 0, 388, 387, 1, 0, 0, 0, 389, 390, 1, 0, 0, 0, 390, 391, 5, 56, 0, 0, 391, 55, 1, + 0, 0, 0, 392, 393, 6, 28, -1, 0, 393, 394, 3, 60, 30, 0, 394, 409, 1, 0, 0, 0, 395, 396, + 10, 2, 0, 0, 396, 402, 5, 168, 0, 0, 397, 403, 3, 80, 40, 0, 398, 399, 5, 55, 0, 0, 399, + 400, 3, 32, 16, 0, 400, 401, 5, 56, 0, 0, 401, 403, 1, 0, 0, 0, 402, 397, 1, 0, 0, 0, 402, + 398, 1, 0, 0, 0, 403, 405, 1, 0, 0, 0, 404, 406, 3, 118, 59, 0, 405, 404, 1, 0, 0, 0, 405, + 406, 1, 0, 0, 0, 406, 408, 1, 0, 0, 0, 407, 395, 1, 0, 0, 0, 408, 411, 1, 0, 0, 0, 409, + 407, 1, 0, 0, 0, 409, 410, 1, 0, 0, 0, 410, 57, 1, 0, 0, 0, 411, 409, 1, 0, 0, 0, 412, 413, + 6, 29, -1, 0, 413, 414, 3, 62, 31, 0, 414, 429, 1, 0, 0, 0, 415, 416, 10, 2, 0, 0, 416, + 422, 5, 168, 0, 0, 417, 423, 3, 80, 40, 0, 418, 419, 5, 55, 0, 0, 419, 420, 3, 32, 16, + 0, 420, 421, 5, 56, 0, 0, 421, 423, 1, 0, 0, 0, 422, 417, 1, 0, 0, 0, 422, 418, 1, 0, 0, + 0, 423, 425, 1, 0, 0, 0, 424, 426, 3, 118, 59, 0, 425, 424, 1, 0, 0, 0, 425, 426, 1, 0, + 0, 0, 426, 428, 1, 0, 0, 0, 427, 415, 1, 0, 0, 0, 428, 431, 1, 0, 0, 0, 429, 427, 1, 0, + 0, 0, 429, 430, 1, 0, 0, 0, 430, 59, 1, 0, 0, 0, 431, 429, 1, 0, 0, 0, 432, 444, 3, 64, + 32, 0, 433, 444, 3, 66, 33, 0, 434, 444, 3, 68, 34, 0, 435, 444, 3, 70, 35, 0, 436, 444, + 3, 72, 36, 0, 437, 444, 3, 102, 51, 0, 438, 444, 3, 80, 40, 0, 439, 444, 3, 86, 43, 0, + 440, 444, 3, 88, 44, 0, 441, 444, 3, 18, 9, 0, 442, 444, 3, 20, 10, 0, 443, 432, 1, 0, + 0, 0, 443, 433, 1, 0, 0, 0, 443, 434, 1, 0, 0, 0, 443, 435, 1, 0, 0, 0, 443, 436, 1, 0, + 0, 0, 443, 437, 1, 0, 0, 0, 443, 438, 1, 0, 0, 0, 443, 439, 1, 0, 0, 0, 443, 440, 1, 0, + 0, 0, 443, 441, 1, 0, 0, 0, 443, 442, 1, 0, 0, 0, 444, 61, 1, 0, 0, 0, 445, 456, 3, 64, + 32, 0, 446, 456, 3, 66, 33, 0, 447, 456, 3, 68, 34, 0, 448, 456, 3, 70, 35, 0, 449, 456, + 3, 72, 36, 0, 450, 456, 3, 80, 40, 0, 451, 456, 3, 86, 43, 0, 452, 456, 3, 88, 44, 0, + 453, 456, 3, 18, 9, 0, 454, 456, 3, 20, 10, 0, 455, 445, 1, 0, 0, 0, 455, 446, 1, 0, 0, + 0, 455, 447, 1, 0, 0, 0, 455, 448, 1, 0, 0, 0, 455, 449, 1, 0, 0, 0, 455, 450, 1, 0, 0, + 0, 455, 451, 1, 0, 0, 0, 455, 452, 1, 0, 0, 0, 455, 453, 1, 0, 0, 0, 455, 454, 1, 0, 0, + 0, 456, 63, 1, 0, 0, 0, 457, 458, 5, 51, 0, 0, 458, 459, 3, 32, 16, 0, 459, 460, 5, 52, + 0, 0, 460, 570, 1, 0, 0, 0, 461, 462, 5, 53, 0, 0, 462, 463, 3, 32, 16, 0, 463, 464, 5, + 54, 0, 0, 464, 570, 1, 0, 0, 0, 465, 466, 5, 55, 0, 0, 466, 467, 3, 32, 16, 0, 467, 468, + 5, 56, 0, 0, 468, 570, 1, 0, 0, 0, 469, 470, 5, 57, 0, 0, 470, 471, 3, 32, 16, 0, 471, + 472, 5, 58, 0, 0, 472, 570, 1, 0, 0, 0, 473, 474, 5, 59, 0, 0, 474, 475, 3, 32, 16, 0, + 475, 476, 5, 60, 0, 0, 476, 570, 1, 0, 0, 0, 477, 478, 5, 61, 0, 0, 478, 479, 3, 32, 16, + 0, 479, 480, 5, 62, 0, 0, 480, 570, 1, 0, 0, 0, 481, 482, 5, 63, 0, 0, 482, 483, 3, 32, + 16, 0, 483, 484, 5, 64, 0, 0, 484, 570, 1, 0, 0, 0, 485, 486, 5, 78, 0, 0, 486, 487, 5, + 51, 0, 0, 487, 488, 3, 32, 16, 0, 488, 489, 5, 79, 0, 0, 489, 490, 5, 52, 0, 0, 490, 570, + 1, 0, 0, 0, 491, 492, 5, 78, 0, 0, 492, 493, 5, 53, 0, 0, 493, 494, 3, 32, 16, 0, 494, + 495, 5, 79, 0, 0, 495, 496, 5, 54, 0, 0, 496, 570, 1, 0, 0, 0, 497, 498, 5, 78, 0, 0, 498, + 499, 5, 55, 0, 0, 499, 500, 3, 32, 16, 0, 500, 501, 5, 79, 0, 0, 501, 502, 5, 56, 0, 0, + 502, 570, 1, 0, 0, 0, 503, 504, 5, 78, 0, 0, 504, 505, 5, 57, 0, 0, 505, 506, 3, 32, 16, + 0, 506, 507, 5, 79, 0, 0, 507, 508, 5, 58, 0, 0, 508, 570, 1, 0, 0, 0, 509, 510, 5, 78, + 0, 0, 510, 511, 5, 59, 0, 0, 511, 512, 3, 32, 16, 0, 512, 513, 5, 79, 0, 0, 513, 514, + 5, 60, 0, 0, 514, 570, 1, 0, 0, 0, 515, 516, 5, 78, 0, 0, 516, 517, 5, 61, 0, 0, 517, 518, + 3, 32, 16, 0, 518, 519, 5, 79, 0, 0, 519, 520, 5, 62, 0, 0, 520, 570, 1, 0, 0, 0, 521, + 522, 5, 78, 0, 0, 522, 523, 5, 63, 0, 0, 523, 524, 3, 32, 16, 0, 524, 525, 5, 79, 0, 0, + 525, 526, 5, 64, 0, 0, 526, 570, 1, 0, 0, 0, 527, 528, 5, 80, 0, 0, 528, 529, 5, 51, 0, + 0, 529, 530, 3, 32, 16, 0, 530, 531, 5, 81, 0, 0, 531, 532, 5, 52, 0, 0, 532, 570, 1, + 0, 0, 0, 533, 534, 5, 80, 0, 0, 534, 535, 5, 53, 0, 0, 535, 536, 3, 32, 16, 0, 536, 537, + 5, 81, 0, 0, 537, 538, 5, 54, 0, 0, 538, 570, 1, 0, 0, 0, 539, 540, 5, 80, 0, 0, 540, 541, + 5, 55, 0, 0, 541, 542, 3, 32, 16, 0, 542, 543, 5, 81, 0, 0, 543, 544, 5, 56, 0, 0, 544, + 570, 1, 0, 0, 0, 545, 546, 5, 80, 0, 0, 546, 547, 5, 57, 0, 0, 547, 548, 3, 32, 16, 0, + 548, 549, 5, 81, 0, 0, 549, 550, 5, 58, 0, 0, 550, 570, 1, 0, 0, 0, 551, 552, 5, 80, 0, + 0, 552, 553, 5, 59, 0, 0, 553, 554, 3, 32, 16, 0, 554, 555, 5, 81, 0, 0, 555, 556, 5, + 60, 0, 0, 556, 570, 1, 0, 0, 0, 557, 558, 5, 80, 0, 0, 558, 559, 5, 61, 0, 0, 559, 560, + 3, 32, 16, 0, 560, 561, 5, 81, 0, 0, 561, 562, 5, 62, 0, 0, 562, 570, 1, 0, 0, 0, 563, + 564, 5, 80, 0, 0, 564, 565, 5, 63, 0, 0, 565, 566, 3, 32, 16, 0, 566, 567, 5, 81, 0, 0, + 567, 568, 5, 64, 0, 0, 568, 570, 1, 0, 0, 0, 569, 457, 1, 0, 0, 0, 569, 461, 1, 0, 0, 0, + 569, 465, 1, 0, 0, 0, 569, 469, 1, 0, 0, 0, 569, 473, 1, 0, 0, 0, 569, 477, 1, 0, 0, 0, + 569, 481, 1, 0, 0, 0, 569, 485, 1, 0, 0, 0, 569, 491, 1, 0, 0, 0, 569, 497, 1, 0, 0, 0, + 569, 503, 1, 0, 0, 0, 569, 509, 1, 0, 0, 0, 569, 515, 1, 0, 0, 0, 569, 521, 1, 0, 0, 0, + 569, 527, 1, 0, 0, 0, 569, 533, 1, 0, 0, 0, 569, 539, 1, 0, 0, 0, 569, 545, 1, 0, 0, 0, + 569, 551, 1, 0, 0, 0, 569, 557, 1, 0, 0, 0, 569, 563, 1, 0, 0, 0, 570, 65, 1, 0, 0, 0, 571, + 572, 5, 69, 0, 0, 572, 573, 3, 32, 16, 0, 573, 574, 5, 69, 0, 0, 574, 588, 1, 0, 0, 0, + 575, 576, 5, 78, 0, 0, 576, 577, 5, 69, 0, 0, 577, 578, 3, 32, 16, 0, 578, 579, 5, 79, + 0, 0, 579, 580, 5, 69, 0, 0, 580, 588, 1, 0, 0, 0, 581, 582, 5, 80, 0, 0, 582, 583, 5, + 69, 0, 0, 583, 584, 3, 32, 16, 0, 584, 585, 5, 81, 0, 0, 585, 586, 5, 69, 0, 0, 586, 588, + 1, 0, 0, 0, 587, 571, 1, 0, 0, 0, 587, 575, 1, 0, 0, 0, 587, 581, 1, 0, 0, 0, 588, 67, 1, + 0, 0, 0, 589, 590, 5, 65, 0, 0, 590, 591, 3, 32, 16, 0, 591, 592, 5, 65, 0, 0, 592, 638, + 1, 0, 0, 0, 593, 594, 5, 66, 0, 0, 594, 595, 3, 32, 16, 0, 595, 596, 5, 67, 0, 0, 596, + 638, 1, 0, 0, 0, 597, 598, 5, 68, 0, 0, 598, 599, 3, 32, 16, 0, 599, 600, 5, 68, 0, 0, + 600, 638, 1, 0, 0, 0, 601, 602, 5, 78, 0, 0, 602, 603, 5, 65, 0, 0, 603, 604, 3, 32, 16, + 0, 604, 605, 5, 79, 0, 0, 605, 606, 5, 65, 0, 0, 606, 638, 1, 0, 0, 0, 607, 608, 5, 78, + 0, 0, 608, 609, 5, 66, 0, 0, 609, 610, 3, 32, 16, 0, 610, 611, 5, 79, 0, 0, 611, 612, + 5, 67, 0, 0, 612, 638, 1, 0, 0, 0, 613, 614, 5, 78, 0, 0, 614, 615, 5, 68, 0, 0, 615, 616, + 3, 32, 16, 0, 616, 617, 5, 79, 0, 0, 617, 618, 5, 68, 0, 0, 618, 638, 1, 0, 0, 0, 619, + 620, 5, 80, 0, 0, 620, 621, 5, 65, 0, 0, 621, 622, 3, 32, 16, 0, 622, 623, 5, 81, 0, 0, + 623, 624, 5, 65, 0, 0, 624, 638, 1, 0, 0, 0, 625, 626, 5, 80, 0, 0, 626, 627, 5, 66, 0, + 0, 627, 628, 3, 32, 16, 0, 628, 629, 5, 81, 0, 0, 629, 630, 5, 67, 0, 0, 630, 638, 1, + 0, 0, 0, 631, 632, 5, 80, 0, 0, 632, 633, 5, 68, 0, 0, 633, 634, 3, 32, 16, 0, 634, 635, + 5, 81, 0, 0, 635, 636, 5, 68, 0, 0, 636, 638, 1, 0, 0, 0, 637, 589, 1, 0, 0, 0, 637, 593, + 1, 0, 0, 0, 637, 597, 1, 0, 0, 0, 637, 601, 1, 0, 0, 0, 637, 607, 1, 0, 0, 0, 637, 613, + 1, 0, 0, 0, 637, 619, 1, 0, 0, 0, 637, 625, 1, 0, 0, 0, 637, 631, 1, 0, 0, 0, 638, 69, 1, + 0, 0, 0, 639, 640, 5, 70, 0, 0, 640, 641, 3, 32, 16, 0, 641, 642, 5, 71, 0, 0, 642, 672, + 1, 0, 0, 0, 643, 644, 5, 72, 0, 0, 644, 645, 3, 32, 16, 0, 645, 646, 5, 73, 0, 0, 646, + 672, 1, 0, 0, 0, 647, 648, 5, 78, 0, 0, 648, 649, 5, 70, 0, 0, 649, 650, 3, 32, 16, 0, + 650, 651, 5, 79, 0, 0, 651, 652, 5, 71, 0, 0, 652, 672, 1, 0, 0, 0, 653, 654, 5, 78, 0, + 0, 654, 655, 5, 72, 0, 0, 655, 656, 3, 32, 16, 0, 656, 657, 5, 79, 0, 0, 657, 658, 5, + 73, 0, 0, 658, 672, 1, 0, 0, 0, 659, 660, 5, 80, 0, 0, 660, 661, 5, 70, 0, 0, 661, 662, + 3, 32, 16, 0, 662, 663, 5, 81, 0, 0, 663, 664, 5, 71, 0, 0, 664, 672, 1, 0, 0, 0, 665, + 666, 5, 80, 0, 0, 666, 667, 5, 72, 0, 0, 667, 668, 3, 32, 16, 0, 668, 669, 5, 81, 0, 0, + 669, 670, 5, 73, 0, 0, 670, 672, 1, 0, 0, 0, 671, 639, 1, 0, 0, 0, 671, 643, 1, 0, 0, 0, + 671, 647, 1, 0, 0, 0, 671, 653, 1, 0, 0, 0, 671, 659, 1, 0, 0, 0, 671, 665, 1, 0, 0, 0, + 672, 71, 1, 0, 0, 0, 673, 674, 5, 74, 0, 0, 674, 675, 3, 32, 16, 0, 675, 676, 5, 75, 0, + 0, 676, 706, 1, 0, 0, 0, 677, 678, 5, 76, 0, 0, 678, 679, 3, 32, 16, 0, 679, 680, 5, 77, + 0, 0, 680, 706, 1, 0, 0, 0, 681, 682, 5, 78, 0, 0, 682, 683, 5, 74, 0, 0, 683, 684, 3, + 32, 16, 0, 684, 685, 5, 79, 0, 0, 685, 686, 5, 75, 0, 0, 686, 706, 1, 0, 0, 0, 687, 688, + 5, 78, 0, 0, 688, 689, 5, 76, 0, 0, 689, 690, 3, 32, 16, 0, 690, 691, 5, 79, 0, 0, 691, + 692, 5, 77, 0, 0, 692, 706, 1, 0, 0, 0, 693, 694, 5, 80, 0, 0, 694, 695, 5, 74, 0, 0, 695, + 696, 3, 32, 16, 0, 696, 697, 5, 81, 0, 0, 697, 698, 5, 75, 0, 0, 698, 706, 1, 0, 0, 0, + 699, 700, 5, 80, 0, 0, 700, 701, 5, 76, 0, 0, 701, 702, 3, 32, 16, 0, 702, 703, 5, 81, + 0, 0, 703, 704, 5, 77, 0, 0, 704, 706, 1, 0, 0, 0, 705, 673, 1, 0, 0, 0, 705, 677, 1, 0, + 0, 0, 705, 681, 1, 0, 0, 0, 705, 687, 1, 0, 0, 0, 705, 693, 1, 0, 0, 0, 705, 699, 1, 0, + 0, 0, 706, 73, 1, 0, 0, 0, 707, 708, 3, 0, 0, 0, 708, 709, 5, 55, 0, 0, 709, 710, 3, 32, + 16, 0, 710, 711, 5, 56, 0, 0, 711, 75, 1, 0, 0, 0, 712, 717, 5, 176, 0, 0, 713, 717, 5, + 191, 0, 0, 714, 717, 5, 192, 0, 0, 715, 717, 3, 74, 37, 0, 716, 712, 1, 0, 0, 0, 716, + 713, 1, 0, 0, 0, 716, 714, 1, 0, 0, 0, 716, 715, 1, 0, 0, 0, 717, 719, 1, 0, 0, 0, 718, + 720, 3, 118, 59, 0, 719, 718, 1, 0, 0, 0, 719, 720, 1, 0, 0, 0, 720, 77, 1, 0, 0, 0, 721, + 726, 5, 176, 0, 0, 722, 726, 5, 191, 0, 0, 723, 726, 5, 192, 0, 0, 724, 726, 3, 74, 37, + 0, 725, 721, 1, 0, 0, 0, 725, 722, 1, 0, 0, 0, 725, 723, 1, 0, 0, 0, 725, 724, 1, 0, 0, + 0, 726, 735, 1, 0, 0, 0, 727, 728, 3, 120, 60, 0, 728, 729, 3, 118, 59, 0, 729, 736, + 1, 0, 0, 0, 730, 731, 3, 118, 59, 0, 731, 732, 3, 120, 60, 0, 732, 736, 1, 0, 0, 0, 733, + 736, 3, 118, 59, 0, 734, 736, 3, 120, 60, 0, 735, 727, 1, 0, 0, 0, 735, 730, 1, 0, 0, + 0, 735, 733, 1, 0, 0, 0, 735, 734, 1, 0, 0, 0, 735, 736, 1, 0, 0, 0, 736, 79, 1, 0, 0, 0, + 737, 746, 3, 78, 39, 0, 738, 746, 5, 193, 0, 0, 739, 746, 5, 179, 0, 0, 740, 746, 5, + 190, 0, 0, 741, 746, 5, 180, 0, 0, 742, 746, 5, 173, 0, 0, 743, 746, 3, 82, 41, 0, 744, + 746, 5, 194, 0, 0, 745, 737, 1, 0, 0, 0, 745, 738, 1, 0, 0, 0, 745, 739, 1, 0, 0, 0, 745, + 740, 1, 0, 0, 0, 745, 741, 1, 0, 0, 0, 745, 742, 1, 0, 0, 0, 745, 743, 1, 0, 0, 0, 745, + 744, 1, 0, 0, 0, 746, 81, 1, 0, 0, 0, 747, 748, 5, 154, 0, 0, 748, 749, 5, 55, 0, 0, 749, + 750, 3, 84, 42, 0, 750, 751, 5, 56, 0, 0, 751, 83, 1, 0, 0, 0, 752, 754, 7, 6, 0, 0, 753, + 752, 1, 0, 0, 0, 754, 755, 1, 0, 0, 0, 755, 753, 1, 0, 0, 0, 755, 756, 1, 0, 0, 0, 756, + 85, 1, 0, 0, 0, 757, 758, 5, 150, 0, 0, 758, 759, 5, 55, 0, 0, 759, 760, 3, 32, 16, 0, + 760, 761, 5, 56, 0, 0, 761, 762, 5, 55, 0, 0, 762, 763, 3, 32, 16, 0, 763, 764, 5, 56, + 0, 0, 764, 87, 1, 0, 0, 0, 765, 766, 5, 55, 0, 0, 766, 767, 3, 32, 16, 0, 767, 768, 5, + 152, 0, 0, 768, 769, 3, 32, 16, 0, 769, 770, 5, 56, 0, 0, 770, 780, 1, 0, 0, 0, 771, 772, + 5, 151, 0, 0, 772, 773, 5, 55, 0, 0, 773, 774, 3, 32, 16, 0, 774, 775, 5, 56, 0, 0, 775, + 776, 5, 55, 0, 0, 776, 777, 3, 32, 16, 0, 777, 778, 5, 56, 0, 0, 778, 780, 1, 0, 0, 0, + 779, 765, 1, 0, 0, 0, 779, 771, 1, 0, 0, 0, 780, 89, 1, 0, 0, 0, 781, 782, 7, 7, 0, 0, 782, + 91, 1, 0, 0, 0, 783, 784, 7, 8, 0, 0, 784, 93, 1, 0, 0, 0, 785, 786, 7, 9, 0, 0, 786, 95, + 1, 0, 0, 0, 787, 788, 7, 10, 0, 0, 788, 97, 1, 0, 0, 0, 789, 796, 3, 90, 45, 0, 790, 791, + 5, 155, 0, 0, 791, 792, 5, 55, 0, 0, 792, 793, 3, 94, 47, 0, 793, 794, 5, 56, 0, 0, 794, + 796, 1, 0, 0, 0, 795, 789, 1, 0, 0, 0, 795, 790, 1, 0, 0, 0, 796, 99, 1, 0, 0, 0, 797, 804, + 3, 92, 46, 0, 798, 799, 5, 155, 0, 0, 799, 800, 5, 55, 0, 0, 800, 801, 3, 96, 48, 0, 801, + 802, 5, 56, 0, 0, 802, 804, 1, 0, 0, 0, 803, 797, 1, 0, 0, 0, 803, 798, 1, 0, 0, 0, 804, + 101, 1, 0, 0, 0, 805, 818, 3, 98, 49, 0, 806, 808, 3, 118, 59, 0, 807, 806, 1, 0, 0, 0, + 807, 808, 1, 0, 0, 0, 808, 810, 1, 0, 0, 0, 809, 811, 3, 120, 60, 0, 810, 809, 1, 0, 0, + 0, 810, 811, 1, 0, 0, 0, 811, 819, 1, 0, 0, 0, 812, 814, 3, 120, 60, 0, 813, 812, 1, 0, + 0, 0, 813, 814, 1, 0, 0, 0, 814, 816, 1, 0, 0, 0, 815, 817, 3, 118, 59, 0, 816, 815, 1, + 0, 0, 0, 816, 817, 1, 0, 0, 0, 817, 819, 1, 0, 0, 0, 818, 807, 1, 0, 0, 0, 818, 813, 1, + 0, 0, 0, 819, 841, 1, 0, 0, 0, 820, 822, 5, 78, 0, 0, 821, 820, 1, 0, 0, 0, 821, 822, 1, + 0, 0, 0, 822, 823, 1, 0, 0, 0, 823, 824, 5, 51, 0, 0, 824, 826, 3, 110, 55, 0, 825, 827, + 5, 79, 0, 0, 826, 825, 1, 0, 0, 0, 826, 827, 1, 0, 0, 0, 827, 828, 1, 0, 0, 0, 828, 829, + 5, 52, 0, 0, 829, 842, 1, 0, 0, 0, 830, 832, 5, 80, 0, 0, 831, 830, 1, 0, 0, 0, 831, 832, + 1, 0, 0, 0, 832, 833, 1, 0, 0, 0, 833, 834, 5, 51, 0, 0, 834, 836, 3, 110, 55, 0, 835, + 837, 5, 81, 0, 0, 836, 835, 1, 0, 0, 0, 836, 837, 1, 0, 0, 0, 837, 838, 1, 0, 0, 0, 838, + 839, 5, 52, 0, 0, 839, 842, 1, 0, 0, 0, 840, 842, 3, 112, 56, 0, 841, 821, 1, 0, 0, 0, + 841, 831, 1, 0, 0, 0, 841, 840, 1, 0, 0, 0, 842, 972, 1, 0, 0, 0, 843, 856, 3, 100, 50, + 0, 844, 846, 3, 118, 59, 0, 845, 844, 1, 0, 0, 0, 845, 846, 1, 0, 0, 0, 846, 848, 1, 0, + 0, 0, 847, 849, 3, 120, 60, 0, 848, 847, 1, 0, 0, 0, 848, 849, 1, 0, 0, 0, 849, 857, 1, + 0, 0, 0, 850, 852, 3, 120, 60, 0, 851, 850, 1, 0, 0, 0, 851, 852, 1, 0, 0, 0, 852, 854, + 1, 0, 0, 0, 853, 855, 3, 118, 59, 0, 854, 853, 1, 0, 0, 0, 854, 855, 1, 0, 0, 0, 855, 857, + 1, 0, 0, 0, 856, 845, 1, 0, 0, 0, 856, 851, 1, 0, 0, 0, 857, 879, 1, 0, 0, 0, 858, 860, + 5, 78, 0, 0, 859, 858, 1, 0, 0, 0, 859, 860, 1, 0, 0, 0, 860, 861, 1, 0, 0, 0, 861, 862, + 5, 51, 0, 0, 862, 864, 3, 114, 57, 0, 863, 865, 5, 79, 0, 0, 864, 863, 1, 0, 0, 0, 864, + 865, 1, 0, 0, 0, 865, 866, 1, 0, 0, 0, 866, 867, 5, 52, 0, 0, 867, 880, 1, 0, 0, 0, 868, + 870, 5, 80, 0, 0, 869, 868, 1, 0, 0, 0, 869, 870, 1, 0, 0, 0, 870, 871, 1, 0, 0, 0, 871, + 872, 5, 51, 0, 0, 872, 874, 3, 114, 57, 0, 873, 875, 5, 81, 0, 0, 874, 873, 1, 0, 0, 0, + 874, 875, 1, 0, 0, 0, 875, 876, 1, 0, 0, 0, 876, 877, 5, 52, 0, 0, 877, 880, 1, 0, 0, 0, + 878, 880, 3, 116, 58, 0, 879, 859, 1, 0, 0, 0, 879, 869, 1, 0, 0, 0, 879, 878, 1, 0, 0, + 0, 880, 972, 1, 0, 0, 0, 881, 883, 3, 76, 38, 0, 882, 884, 3, 120, 60, 0, 883, 882, 1, + 0, 0, 0, 883, 884, 1, 0, 0, 0, 884, 886, 1, 0, 0, 0, 885, 887, 5, 78, 0, 0, 886, 885, 1, + 0, 0, 0, 886, 887, 1, 0, 0, 0, 887, 888, 1, 0, 0, 0, 888, 889, 7, 11, 0, 0, 889, 890, 3, + 106, 53, 0, 890, 892, 7, 12, 0, 0, 891, 893, 5, 79, 0, 0, 892, 891, 1, 0, 0, 0, 892, 893, + 1, 0, 0, 0, 893, 972, 1, 0, 0, 0, 894, 896, 3, 76, 38, 0, 895, 897, 3, 120, 60, 0, 896, + 895, 1, 0, 0, 0, 896, 897, 1, 0, 0, 0, 897, 898, 1, 0, 0, 0, 898, 900, 5, 55, 0, 0, 899, + 901, 5, 78, 0, 0, 900, 899, 1, 0, 0, 0, 900, 901, 1, 0, 0, 0, 901, 902, 1, 0, 0, 0, 902, + 903, 7, 11, 0, 0, 903, 904, 3, 106, 53, 0, 904, 906, 7, 12, 0, 0, 905, 907, 5, 79, 0, + 0, 906, 905, 1, 0, 0, 0, 906, 907, 1, 0, 0, 0, 907, 908, 1, 0, 0, 0, 908, 909, 5, 56, 0, + 0, 909, 972, 1, 0, 0, 0, 910, 931, 5, 84, 0, 0, 911, 912, 3, 118, 59, 0, 912, 913, 3, + 120, 60, 0, 913, 932, 1, 0, 0, 0, 914, 915, 3, 120, 60, 0, 915, 916, 3, 118, 59, 0, 916, + 932, 1, 0, 0, 0, 917, 918, 5, 167, 0, 0, 918, 919, 5, 55, 0, 0, 919, 920, 5, 56, 0, 0, + 920, 921, 1, 0, 0, 0, 921, 922, 5, 168, 0, 0, 922, 923, 5, 55, 0, 0, 923, 932, 5, 56, + 0, 0, 924, 925, 5, 168, 0, 0, 925, 926, 5, 55, 0, 0, 926, 927, 5, 56, 0, 0, 927, 928, + 1, 0, 0, 0, 928, 929, 5, 167, 0, 0, 929, 930, 5, 55, 0, 0, 930, 932, 5, 56, 0, 0, 931, + 911, 1, 0, 0, 0, 931, 914, 1, 0, 0, 0, 931, 917, 1, 0, 0, 0, 931, 924, 1, 0, 0, 0, 931, + 932, 1, 0, 0, 0, 932, 939, 1, 0, 0, 0, 933, 935, 3, 34, 17, 0, 934, 933, 1, 0, 0, 0, 934, + 935, 1, 0, 0, 0, 935, 936, 1, 0, 0, 0, 936, 940, 5, 173, 0, 0, 937, 940, 3, 86, 43, 0, + 938, 940, 3, 34, 17, 0, 939, 934, 1, 0, 0, 0, 939, 937, 1, 0, 0, 0, 939, 938, 1, 0, 0, + 0, 940, 972, 1, 0, 0, 0, 941, 946, 5, 121, 0, 0, 942, 943, 5, 61, 0, 0, 943, 944, 3, 32, + 16, 0, 944, 945, 5, 62, 0, 0, 945, 947, 1, 0, 0, 0, 946, 942, 1, 0, 0, 0, 946, 947, 1, + 0, 0, 0, 947, 948, 1, 0, 0, 0, 948, 949, 5, 55, 0, 0, 949, 950, 3, 32, 16, 0, 950, 951, + 5, 56, 0, 0, 951, 972, 1, 0, 0, 0, 952, 959, 7, 13, 0, 0, 953, 954, 3, 122, 61, 0, 954, + 955, 3, 120, 60, 0, 955, 960, 1, 0, 0, 0, 956, 957, 3, 120, 60, 0, 957, 958, 3, 122, + 61, 0, 958, 960, 1, 0, 0, 0, 959, 953, 1, 0, 0, 0, 959, 956, 1, 0, 0, 0, 960, 961, 1, 0, + 0, 0, 961, 962, 3, 36, 18, 0, 962, 972, 1, 0, 0, 0, 963, 964, 5, 82, 0, 0, 964, 965, 3, + 108, 54, 0, 965, 966, 3, 36, 18, 0, 966, 972, 1, 0, 0, 0, 967, 969, 5, 174, 0, 0, 968, + 970, 3, 120, 60, 0, 969, 968, 1, 0, 0, 0, 969, 970, 1, 0, 0, 0, 970, 972, 1, 0, 0, 0, 971, + 805, 1, 0, 0, 0, 971, 843, 1, 0, 0, 0, 971, 881, 1, 0, 0, 0, 971, 894, 1, 0, 0, 0, 971, + 910, 1, 0, 0, 0, 971, 941, 1, 0, 0, 0, 971, 952, 1, 0, 0, 0, 971, 963, 1, 0, 0, 0, 971, + 967, 1, 0, 0, 0, 972, 103, 1, 0, 0, 0, 973, 974, 3, 32, 16, 0, 974, 975, 5, 171, 0, 0, + 975, 976, 3, 104, 52, 0, 976, 979, 1, 0, 0, 0, 977, 979, 3, 32, 16, 0, 978, 973, 1, 0, + 0, 0, 978, 977, 1, 0, 0, 0, 979, 105, 1, 0, 0, 0, 980, 989, 3, 80, 40, 0, 981, 982, 3, + 32, 16, 0, 982, 983, 5, 171, 0, 0, 983, 989, 1, 0, 0, 0, 984, 985, 3, 32, 16, 0, 985, + 986, 5, 171, 0, 0, 986, 987, 3, 104, 52, 0, 987, 989, 1, 0, 0, 0, 988, 980, 1, 0, 0, 0, + 988, 981, 1, 0, 0, 0, 988, 984, 1, 0, 0, 0, 989, 107, 1, 0, 0, 0, 990, 991, 5, 167, 0, + 0, 991, 992, 5, 55, 0, 0, 992, 993, 7, 14, 0, 0, 993, 994, 5, 83, 0, 0, 994, 999, 3, 32, + 16, 0, 995, 996, 5, 168, 0, 0, 996, 997, 5, 55, 0, 0, 997, 998, 7, 4, 0, 0, 998, 1000, + 5, 56, 0, 0, 999, 995, 1, 0, 0, 0, 999, 1000, 1, 0, 0, 0, 1000, 1001, 1, 0, 0, 0, 1001, + 1002, 5, 56, 0, 0, 1002, 109, 1, 0, 0, 0, 1003, 1004, 3, 32, 16, 0, 1004, 111, 1, 0, + 0, 0, 1005, 1006, 3, 38, 19, 0, 1006, 113, 1, 0, 0, 0, 1007, 1013, 3, 32, 16, 0, 1008, + 1009, 3, 32, 16, 0, 1009, 1010, 5, 171, 0, 0, 1010, 1011, 3, 114, 57, 0, 1011, 1013, + 1, 0, 0, 0, 1012, 1007, 1, 0, 0, 0, 1012, 1008, 1, 0, 0, 0, 1013, 115, 1, 0, 0, 0, 1014, + 1015, 3, 38, 19, 0, 1015, 117, 1, 0, 0, 0, 1016, 1025, 5, 167, 0, 0, 1017, 1026, 3, + 80, 40, 0, 1018, 1021, 5, 55, 0, 0, 1019, 1022, 3, 32, 16, 0, 1020, 1022, 3, 104, 52, + 0, 1021, 1019, 1, 0, 0, 0, 1021, 1020, 1, 0, 0, 0, 1022, 1023, 1, 0, 0, 0, 1023, 1024, + 5, 56, 0, 0, 1024, 1026, 1, 0, 0, 0, 1025, 1017, 1, 0, 0, 0, 1025, 1018, 1, 0, 0, 0, 1026, + 119, 1, 0, 0, 0, 1027, 1033, 5, 168, 0, 0, 1028, 1034, 3, 80, 40, 0, 1029, 1030, 5, + 55, 0, 0, 1030, 1031, 3, 32, 16, 0, 1031, 1032, 5, 56, 0, 0, 1032, 1034, 1, 0, 0, 0, + 1033, 1028, 1, 0, 0, 0, 1033, 1029, 1, 0, 0, 0, 1034, 121, 1, 0, 0, 0, 1035, 1036, 5, + 167, 0, 0, 1036, 1037, 5, 55, 0, 0, 1037, 1038, 3, 30, 15, 0, 1038, 1039, 5, 56, 0, + 0, 1039, 123, 1, 0, 0, 0, 1040, 1041, 5, 167, 0, 0, 1041, 1042, 5, 55, 0, 0, 1042, 1043, + 3, 30, 15, 0, 1043, 1044, 5, 56, 0, 0, 1044, 125, 1, 0, 0, 0, 92, 130, 140, 146, 160, + 167, 176, 180, 188, 194, 202, 206, 215, 226, 266, 275, 285, 288, 304, 315, 326, + 334, 336, 344, 347, 353, 360, 366, 374, 380, 388, 402, 405, 409, 422, 425, 429, + 443, 455, 569, 587, 637, 671, 705, 716, 719, 725, 735, 745, 755, 779, 795, 803, + 807, 810, 813, 816, 818, 821, 826, 831, 836, 841, 845, 848, 851, 854, 856, 859, + 864, 869, 874, 879, 883, 886, 892, 896, 900, 906, 931, 934, 939, 946, 959, 969, + 971, 978, 988, 999, 1012, 1021, 1025, 1033 + ] + + +class PSParser (Parser): + + grammarFileName = "PS.g4" + + atn = ATNDeserializer().deserialize(serializedATN()) + + decisionsToDFA = [DFA(ds, i) for i, ds in enumerate(atn.decisionToState)] + + sharedContextCache = PredictionContextCache() + + literalNames = [u"<INVALID>", u"'\\acute'", u"'\\bar'", u"'\\overline'", + u"'\\breve'", u"'\\check'", u"'\\widecheck'", u"'\\dot'", + u"'\\ddot'", u"'\\grave'", u"'\\hat'", u"'\\tilde'", + u"'\\widetilde'", u"'\\vec'", u"'\\overrightarrow'", + u"'\\bm'", u"'\\boldsymbol'", u"'\\text'", u"'\\textit'", + u"'\\mathbb'", u"'\\mathbin'", u"'\\mathbf'", u"'\\mathcal'", + u"'\\mathclap'", u"'\\mathclose'", u"'\\mathellipsis'", + u"'\\mathfrak'", u"'\\mathinner'", u"'\\mathnormal'", + u"'\\mathop'", u"'\\mathopen'", u"'\\mathord'", u"'\\mathpunct'", + u"'\\mathrel'", u"'\\mathring'", u"'\\mathrlap'", u"'\\mathrm'", + u"'\\mathscr'", u"'\\mathsf'", u"'\\mathsterling'", + u"'\\mathtt'", u"'^T'", u"'^{T}'", u"'^{\\top}'", u"'''", + u"<INVALID>", u"'\\$'", u"'+'", u"'-'", u"'*'", u"<INVALID>", + u"'('", u"')'", u"'\\lgroup'", u"'\\rgroup'", u"'{'", + u"'}'", u"'\\{'", u"'\\}'", u"'\\lbrace'", u"'\\rbrace'", + u"'['", u"']'", u"'\\lbrack'", u"'\\rbrack'", u"'|'", + u"'\\lvert'", u"'\\rvert'", u"'\\vert'", u"'\\|'", + u"'\\lfloor'", u"'\\rfloor'", u"'\\llcorner'", u"'\\lrcorner'", + u"'\\lceil'", u"'\\rceil'", u"'\\ulcorner'", u"'\\urcorner'", + u"'\\left'", u"'\\right'", u"'\\mleft'", u"'\\mright'", + u"'\\lim'", u"<INVALID>", u"'\\int'", u"'\\sum'", u"'\\prod'", + u"'\\log'", u"'\\ln'", u"'\\exp'", u"'\\sin'", u"'\\cos'", + u"'\\tan'", u"'\\csc'", u"'\\sec'", u"'\\cot'", u"'\\arcsin'", + u"'\\arccos'", u"'\\arctan'", u"'\\arccsc'", u"'\\arcsec'", + u"'\\arccot'", u"'\\sinh'", u"'\\cosh'", u"'\\tanh'", + u"'\\arsinh'", u"'\\arcosh'", u"'\\artanh'", u"'\\arcsinh'", + u"'\\arccosh'", u"'\\arctanh'", u"'arsinh'", u"'arcsinh'", + u"'arcosh'", u"'arccosh'", u"'artanh'", u"'arctanh'", + u"'gcd'", u"'lcm'", u"'floor'", u"'ceil'", u"'\\sqrt'", + u"'\\gcd'", u"'\\lcm'", u"'\\floor'", u"'\\ceil'", + u"'\\max'", u"'\\min'", u"'\\det'", u"'eye'", u"'zeros'", + u"'ones'", u"'cols'", u"'rows'", u"'diag'", u"'norm'", + u"'rank'", u"<INVALID>", u"'rref'", u"'hstack'", u"'vstack'", + u"<INVALID>", u"'nullspace'", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"'\\times'", u"'\\cdot'", + u"'\\div'", u"'\\frac'", u"<INVALID>", u"'\\choose'", + u"'\\mod'", u"'\\mathit'", u"'\\operatorname'", u"'matrix'", + u"'pmatrix'", u"'bmatrix'", u"'vmatrix'", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"'&'", u"'\\\\'", u"'_'", u"'^'", u"':'", u"';'", + u"','", u"'.'", u"<INVALID>", u"<INVALID>", u"'E'", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"'\\in'", u"'='", u"<INVALID>", u"'<'", + u"<INVALID>", u"'>'", u"<INVALID>", u"<INVALID>", u"'!'"] + + symbolicNames = [u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"<INVALID>", u"<INVALID>", u"<INVALID>", + u"<INVALID>", u"WS", u"DOLLAR_SIGN", u"ADD", u"SUB", + u"MUL", u"DIV", u"L_PAREN", u"R_PAREN", u"L_GROUP", + u"R_GROUP", u"L_BRACE", u"R_BRACE", u"L_BRACE_VISUAL", + u"R_BRACE_VISUAL", u"L_BRACE_CMD", u"R_BRACE_CMD", + u"L_BRACKET", u"R_BRACKET", u"L_BRACK", u"R_BRACK", + u"BAR", u"L_VERT", u"R_VERT", u"VERT", u"NORM", u"L_FLOOR", + u"R_FLOOR", u"LL_CORNER", u"LR_CORNER", u"L_CEIL", + u"R_CEIL", u"UL_CORNER", u"UR_CORNER", u"L_LEFT", + u"R_RIGHT", u"ML_LEFT", u"MR_RIGHT", u"FUNC_LIM", + u"LIM_APPROACH_SYM", u"FUNC_INT", u"FUNC_SUM", u"FUNC_PROD", + u"FUNC_LOG", u"FUNC_LN", u"FUNC_EXP", u"FUNC_SIN", + u"FUNC_COS", u"FUNC_TAN", u"FUNC_CSC", u"FUNC_SEC", + u"FUNC_COT", u"FUNC_ARCSIN", u"FUNC_ARCCOS", u"FUNC_ARCTAN", + u"FUNC_ARCCSC", u"FUNC_ARCSEC", u"FUNC_ARCCOT", u"FUNC_SINH", + u"FUNC_COSH", u"FUNC_TANH", u"FUNC_ARSINH", u"FUNC_ARCOSH", + u"FUNC_ARTANH", u"FUNC_ARCSINH", u"FUNC_ARCCOSH", + u"FUNC_ARCTANH", u"FUNC_ARSINH_NAME", u"FUNC_ARCSINH_NAME", + u"FUNC_ARCOSH_NAME", u"FUNC_ARCCOSH_NAME", u"FUNC_ARTANH_NAME", + u"FUNC_ARCTANH_NAME", u"FUNC_GCD_NAME", u"FUNC_LCM_NAME", + u"FUNC_FLOOR_NAME", u"FUNC_CEIL_NAME", u"FUNC_SQRT", + u"FUNC_GCD", u"FUNC_LCM", u"FUNC_FLOOR", u"FUNC_CEIL", + u"FUNC_MAX", u"FUNC_MIN", u"FUNC_DET", u"FUNC_EYE_NAME", + u"FUNC_ZEROS_NAME", u"FUNC_ONES_NAME", u"FUNC_COLS_NAME", + u"FUNC_ROWS_NAME", u"FUNC_DIAG_NAME", u"FUNC_NORM_NAME", + u"FUNC_RANK_NAME", u"FUNC_TRACE_NAME", u"FUNC_RREF_NAME", + u"FUNC_HSTACK_NAME", u"FUNC_VSTACK_NAME", u"FUNC_ORTHOGONALIZE_NAME", + u"FUNC_NULLSPACE_NAME", u"FUNC_DIAGONALIZE_NAME", + u"FUNC_EIGENVALS_NAME", u"FUNC_EIGENVECTORS_NAME", + u"FUNC_SVD_NAME", u"CMD_TIMES", u"CMD_CDOT", u"CMD_DIV", + u"CMD_FRAC", u"CMD_BINOM", u"CMD_CHOOSE", u"CMD_MOD", + u"CMD_MATHIT", u"CMD_OPERATORNAME", u"MATRIX_TYPE_MATRIX", + u"MATRIX_TYPE_PMATRIX", u"MATRIX_TYPE_BMATRIX", u"MATRIX_TYPE_DET", + u"MATRIX_TYPES", u"CMD_MATRIX_START", u"CMD_MATRIX_END", + u"CMD_DET_START", u"CMD_DET_END", u"MATRIX_DEL_COL", + u"MATRIX_DEL_ROW", u"UNDERSCORE", u"CARET", u"COLON", + u"SEMICOLON", u"COMMA", u"PERIOD", u"DIFFERENTIAL", + u"EXP_E", u"E_NOTATION_E", u"LETTER_NO_E", u"MATRIX_XRIGHTARROW", + u"TRANSFORM_EXCHANGE", u"NUMBER", u"E_NOTATION", u"IN", + u"ASSIGNMENT", u"EQUAL", u"LT", u"LTE", u"GT", u"GTE", + u"UNEQUAL", u"BANG", u"PERCENT_NUMBER", u"GREEK_CMD", + u"OTHER_SYMBOL_CMD", u"SYMBOL", u"VARIABLE"] + + RULE_accent_symbol = 0 + RULE_math = 1 + RULE_transpose = 2 + RULE_transform_atom = 3 + RULE_transform_scale = 4 + RULE_transform_swap = 5 + RULE_transform_assignment = 6 + RULE_elementary_transform = 7 + RULE_elementary_transforms = 8 + RULE_matrix = 9 + RULE_det = 10 + RULE_matrix_row = 11 + RULE_relation = 12 + RULE_relation_list = 13 + RULE_relation_list_content = 14 + RULE_equality = 15 + RULE_expr = 16 + RULE_additive = 17 + RULE_mp = 18 + RULE_mp_nofunc = 19 + RULE_unary = 20 + RULE_unary_nofunc = 21 + RULE_postfix = 22 + RULE_postfix_nofunc = 23 + RULE_postfix_op = 24 + RULE_eval_at = 25 + RULE_eval_at_sub = 26 + RULE_eval_at_sup = 27 + RULE_exp = 28 + RULE_exp_nofunc = 29 + RULE_comp = 30 + RULE_comp_nofunc = 31 + RULE_group = 32 + RULE_norm_group = 33 + RULE_abs_group = 34 + RULE_floor_group = 35 + RULE_ceil_group = 36 + RULE_accent = 37 + RULE_atom_expr_no_supexpr = 38 + RULE_atom_expr = 39 + RULE_atom = 40 + RULE_mathit = 41 + RULE_mathit_text = 42 + RULE_frac = 43 + RULE_binom = 44 + RULE_func_normal_functions_single_arg = 45 + RULE_func_normal_functions_multi_arg = 46 + RULE_func_operator_names_single_arg = 47 + RULE_func_operator_names_multi_arg = 48 + RULE_func_normal_single_arg = 49 + RULE_func_normal_multi_arg = 50 + RULE_func = 51 + RULE_args = 52 + RULE_func_common_args = 53 + RULE_limit_sub = 54 + RULE_func_single_arg = 55 + RULE_func_single_arg_noparens = 56 + RULE_func_multi_arg = 57 + RULE_func_multi_arg_noparens = 58 + RULE_subexpr = 59 + RULE_supexpr = 60 + RULE_subeq = 61 + RULE_supeq = 62 + + ruleNames = [u"accent_symbol", u"math", u"transpose", u"transform_atom", + u"transform_scale", u"transform_swap", u"transform_assignment", + u"elementary_transform", u"elementary_transforms", u"matrix", + u"det", u"matrix_row", u"relation", u"relation_list", + u"relation_list_content", u"equality", u"expr", u"additive", + u"mp", u"mp_nofunc", u"unary", u"unary_nofunc", u"postfix", + u"postfix_nofunc", u"postfix_op", u"eval_at", u"eval_at_sub", + u"eval_at_sup", u"exp", u"exp_nofunc", u"comp", u"comp_nofunc", + u"group", u"norm_group", u"abs_group", u"floor_group", + u"ceil_group", u"accent", u"atom_expr_no_supexpr", u"atom_expr", + u"atom", u"mathit", u"mathit_text", u"frac", u"binom", + u"func_normal_functions_single_arg", u"func_normal_functions_multi_arg", + u"func_operator_names_single_arg", u"func_operator_names_multi_arg", + u"func_normal_single_arg", u"func_normal_multi_arg", + u"func", u"args", u"func_common_args", u"limit_sub", + u"func_single_arg", u"func_single_arg_noparens", u"func_multi_arg", + u"func_multi_arg_noparens", u"subexpr", u"supexpr", u"subeq", + u"supeq"] + + EOF = Token.EOF + T__0 = 1 + T__1 = 2 + T__2 = 3 + T__3 = 4 + T__4 = 5 + T__5 = 6 + T__6 = 7 + T__7 = 8 + T__8 = 9 + T__9 = 10 + T__10 = 11 + T__11 = 12 + T__12 = 13 + T__13 = 14 + T__14 = 15 + T__15 = 16 + T__16 = 17 + T__17 = 18 + T__18 = 19 + T__19 = 20 + T__20 = 21 + T__21 = 22 + T__22 = 23 + T__23 = 24 + T__24 = 25 + T__25 = 26 + T__26 = 27 + T__27 = 28 + T__28 = 29 + T__29 = 30 + T__30 = 31 + T__31 = 32 + T__32 = 33 + T__33 = 34 + T__34 = 35 + T__35 = 36 + T__36 = 37 + T__37 = 38 + T__38 = 39 + T__39 = 40 + T__40 = 41 + T__41 = 42 + T__42 = 43 + T__43 = 44 + WS = 45 + DOLLAR_SIGN = 46 + ADD = 47 + SUB = 48 + MUL = 49 + DIV = 50 + L_PAREN = 51 + R_PAREN = 52 + L_GROUP = 53 + R_GROUP = 54 + L_BRACE = 55 + R_BRACE = 56 + L_BRACE_VISUAL = 57 + R_BRACE_VISUAL = 58 + L_BRACE_CMD = 59 + R_BRACE_CMD = 60 + L_BRACKET = 61 + R_BRACKET = 62 + L_BRACK = 63 + R_BRACK = 64 + BAR = 65 + L_VERT = 66 + R_VERT = 67 + VERT = 68 + NORM = 69 + L_FLOOR = 70 + R_FLOOR = 71 + LL_CORNER = 72 + LR_CORNER = 73 + L_CEIL = 74 + R_CEIL = 75 + UL_CORNER = 76 + UR_CORNER = 77 + L_LEFT = 78 + R_RIGHT = 79 + ML_LEFT = 80 + MR_RIGHT = 81 + FUNC_LIM = 82 + LIM_APPROACH_SYM = 83 + FUNC_INT = 84 + FUNC_SUM = 85 + FUNC_PROD = 86 + FUNC_LOG = 87 + FUNC_LN = 88 + FUNC_EXP = 89 + FUNC_SIN = 90 + FUNC_COS = 91 + FUNC_TAN = 92 + FUNC_CSC = 93 + FUNC_SEC = 94 + FUNC_COT = 95 + FUNC_ARCSIN = 96 + FUNC_ARCCOS = 97 + FUNC_ARCTAN = 98 + FUNC_ARCCSC = 99 + FUNC_ARCSEC = 100 + FUNC_ARCCOT = 101 + FUNC_SINH = 102 + FUNC_COSH = 103 + FUNC_TANH = 104 + FUNC_ARSINH = 105 + FUNC_ARCOSH = 106 + FUNC_ARTANH = 107 + FUNC_ARCSINH = 108 + FUNC_ARCCOSH = 109 + FUNC_ARCTANH = 110 + FUNC_ARSINH_NAME = 111 + FUNC_ARCSINH_NAME = 112 + FUNC_ARCOSH_NAME = 113 + FUNC_ARCCOSH_NAME = 114 + FUNC_ARTANH_NAME = 115 + FUNC_ARCTANH_NAME = 116 + FUNC_GCD_NAME = 117 + FUNC_LCM_NAME = 118 + FUNC_FLOOR_NAME = 119 + FUNC_CEIL_NAME = 120 + FUNC_SQRT = 121 + FUNC_GCD = 122 + FUNC_LCM = 123 + FUNC_FLOOR = 124 + FUNC_CEIL = 125 + FUNC_MAX = 126 + FUNC_MIN = 127 + FUNC_DET = 128 + FUNC_EYE_NAME = 129 + FUNC_ZEROS_NAME = 130 + FUNC_ONES_NAME = 131 + FUNC_COLS_NAME = 132 + FUNC_ROWS_NAME = 133 + FUNC_DIAG_NAME = 134 + FUNC_NORM_NAME = 135 + FUNC_RANK_NAME = 136 + FUNC_TRACE_NAME = 137 + FUNC_RREF_NAME = 138 + FUNC_HSTACK_NAME = 139 + FUNC_VSTACK_NAME = 140 + FUNC_ORTHOGONALIZE_NAME = 141 + FUNC_NULLSPACE_NAME = 142 + FUNC_DIAGONALIZE_NAME = 143 + FUNC_EIGENVALS_NAME = 144 + FUNC_EIGENVECTORS_NAME = 145 + FUNC_SVD_NAME = 146 + CMD_TIMES = 147 + CMD_CDOT = 148 + CMD_DIV = 149 + CMD_FRAC = 150 + CMD_BINOM = 151 + CMD_CHOOSE = 152 + CMD_MOD = 153 + CMD_MATHIT = 154 + CMD_OPERATORNAME = 155 + MATRIX_TYPE_MATRIX = 156 + MATRIX_TYPE_PMATRIX = 157 + MATRIX_TYPE_BMATRIX = 158 + MATRIX_TYPE_DET = 159 + MATRIX_TYPES = 160 + CMD_MATRIX_START = 161 + CMD_MATRIX_END = 162 + CMD_DET_START = 163 + CMD_DET_END = 164 + MATRIX_DEL_COL = 165 + MATRIX_DEL_ROW = 166 + UNDERSCORE = 167 + CARET = 168 + COLON = 169 + SEMICOLON = 170 + COMMA = 171 + PERIOD = 172 + DIFFERENTIAL = 173 + EXP_E = 174 + E_NOTATION_E = 175 + LETTER_NO_E = 176 + MATRIX_XRIGHTARROW = 177 + TRANSFORM_EXCHANGE = 178 + NUMBER = 179 + E_NOTATION = 180 + IN = 181 + ASSIGNMENT = 182 + EQUAL = 183 + LT = 184 + LTE = 185 + GT = 186 + GTE = 187 + UNEQUAL = 188 + BANG = 189 + PERCENT_NUMBER = 190 + GREEK_CMD = 191 + OTHER_SYMBOL_CMD = 192 + SYMBOL = 193 + VARIABLE = 194 + + def __init__(self, input, output=sys.stdout): + super(PSParser, self).__init__(input, output=output) + self.checkVersion("4.11.1") + self._interp = ParserATNSimulator(self, self.atn, self.decisionsToDFA, self.sharedContextCache) + self._predicates = None + + class Accent_symbolContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Accent_symbolContext, self).__init__(parent, invokingState) + self.parser = parser + + def CMD_MATHIT(self): + return self.getToken(PSParser.CMD_MATHIT, 0) + + def getRuleIndex(self): + return PSParser.RULE_accent_symbol + + def enterRule(self, listener): + if hasattr(listener, "enterAccent_symbol"): + listener.enterAccent_symbol(self) + + def exitRule(self, listener): + if hasattr(listener, "exitAccent_symbol"): + listener.exitAccent_symbol(self) + + def accent_symbol(self): + + localctx = PSParser.Accent_symbolContext(self, self._ctx, self.state) + self.enterRule(localctx, 0, self.RULE_accent_symbol) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 126 + _la = self._input.LA(1) + if not(((_la) & ~0x3f) == 0 and ((1 << _la) & 2199023255550) != 0 or _la == 154): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class MathContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.MathContext, self).__init__(parent, invokingState) + self.parser = parser + + def relation(self): + return self.getTypedRuleContext(PSParser.RelationContext, 0) + + def relation_list(self): + return self.getTypedRuleContext(PSParser.Relation_listContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_math + + def enterRule(self, listener): + if hasattr(listener, "enterMath"): + listener.enterMath(self) + + def exitRule(self, listener): + if hasattr(listener, "exitMath"): + listener.exitMath(self) + + def math(self): + + localctx = PSParser.MathContext(self, self._ctx, self.state) + self.enterRule(localctx, 2, self.RULE_math) + try: + self.state = 130 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 0, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 128 + self.relation(0) + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 129 + self.relation_list() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class TransposeContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.TransposeContext, self).__init__(parent, invokingState) + self.parser = parser + + def getRuleIndex(self): + return PSParser.RULE_transpose + + def enterRule(self, listener): + if hasattr(listener, "enterTranspose"): + listener.enterTranspose(self) + + def exitRule(self, listener): + if hasattr(listener, "exitTranspose"): + listener.exitTranspose(self) + + def transpose(self): + + localctx = PSParser.TransposeContext(self, self._ctx, self.state) + self.enterRule(localctx, 4, self.RULE_transpose) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 132 + _la = self._input.LA(1) + if not(((_la) & ~0x3f) == 0 and ((1 << _la) & 32985348833280) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Transform_atomContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Transform_atomContext, self).__init__(parent, invokingState) + self.parser = parser + + def LETTER_NO_E(self): + return self.getToken(PSParser.LETTER_NO_E, 0) + + def UNDERSCORE(self): + return self.getToken(PSParser.UNDERSCORE, 0) + + def NUMBER(self): + return self.getToken(PSParser.NUMBER, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def getRuleIndex(self): + return PSParser.RULE_transform_atom + + def enterRule(self, listener): + if hasattr(listener, "enterTransform_atom"): + listener.enterTransform_atom(self) + + def exitRule(self, listener): + if hasattr(listener, "exitTransform_atom"): + listener.exitTransform_atom(self) + + def transform_atom(self): + + localctx = PSParser.Transform_atomContext(self, self._ctx, self.state) + self.enterRule(localctx, 6, self.RULE_transform_atom) + try: + self.enterOuterAlt(localctx, 1) + self.state = 134 + self.match(PSParser.LETTER_NO_E) + self.state = 135 + self.match(PSParser.UNDERSCORE) + self.state = 140 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [179]: + self.state = 136 + self.match(PSParser.NUMBER) + pass + elif token in [55]: + self.state = 137 + self.match(PSParser.L_BRACE) + self.state = 138 + self.match(PSParser.NUMBER) + self.state = 139 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Transform_scaleContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Transform_scaleContext, self).__init__(parent, invokingState) + self.parser = parser + + def transform_atom(self): + return self.getTypedRuleContext(PSParser.Transform_atomContext, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def group(self): + return self.getTypedRuleContext(PSParser.GroupContext, 0) + + def ADD(self): + return self.getToken(PSParser.ADD, 0) + + def SUB(self): + return self.getToken(PSParser.SUB, 0) + + def getRuleIndex(self): + return PSParser.RULE_transform_scale + + def enterRule(self, listener): + if hasattr(listener, "enterTransform_scale"): + listener.enterTransform_scale(self) + + def exitRule(self, listener): + if hasattr(listener, "exitTransform_scale"): + listener.exitTransform_scale(self) + + def transform_scale(self): + + localctx = PSParser.Transform_scaleContext(self, self._ctx, self.state) + self.enterRule(localctx, 8, self.RULE_transform_scale) + try: + self.enterOuterAlt(localctx, 1) + self.state = 146 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 2, self._ctx) + if la_ == 1: + self.state = 142 + self.expr() + pass + + elif la_ == 2: + self.state = 143 + self.group() + pass + + elif la_ == 3: + self.state = 144 + self.match(PSParser.ADD) + pass + + elif la_ == 4: + self.state = 145 + self.match(PSParser.SUB) + pass + + self.state = 148 + self.transform_atom() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Transform_swapContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Transform_swapContext, self).__init__(parent, invokingState) + self.parser = parser + + def transform_atom(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Transform_atomContext) + else: + return self.getTypedRuleContext(PSParser.Transform_atomContext, i) + + def TRANSFORM_EXCHANGE(self): + return self.getToken(PSParser.TRANSFORM_EXCHANGE, 0) + + def getRuleIndex(self): + return PSParser.RULE_transform_swap + + def enterRule(self, listener): + if hasattr(listener, "enterTransform_swap"): + listener.enterTransform_swap(self) + + def exitRule(self, listener): + if hasattr(listener, "exitTransform_swap"): + listener.exitTransform_swap(self) + + def transform_swap(self): + + localctx = PSParser.Transform_swapContext(self, self._ctx, self.state) + self.enterRule(localctx, 10, self.RULE_transform_swap) + try: + self.enterOuterAlt(localctx, 1) + self.state = 150 + self.transform_atom() + self.state = 151 + self.match(PSParser.TRANSFORM_EXCHANGE) + self.state = 152 + self.transform_atom() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Transform_assignmentContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Transform_assignmentContext, self).__init__(parent, invokingState) + self.parser = parser + + def transform_atom(self): + return self.getTypedRuleContext(PSParser.Transform_atomContext, 0) + + def transform_scale(self): + return self.getTypedRuleContext(PSParser.Transform_scaleContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_transform_assignment + + def enterRule(self, listener): + if hasattr(listener, "enterTransform_assignment"): + listener.enterTransform_assignment(self) + + def exitRule(self, listener): + if hasattr(listener, "exitTransform_assignment"): + listener.exitTransform_assignment(self) + + def transform_assignment(self): + + localctx = PSParser.Transform_assignmentContext(self, self._ctx, self.state) + self.enterRule(localctx, 12, self.RULE_transform_assignment) + try: + self.enterOuterAlt(localctx, 1) + self.state = 154 + self.transform_atom() + self.state = 155 + self.transform_scale() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Elementary_transformContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Elementary_transformContext, self).__init__(parent, invokingState) + self.parser = parser + + def transform_assignment(self): + return self.getTypedRuleContext(PSParser.Transform_assignmentContext, 0) + + def transform_scale(self): + return self.getTypedRuleContext(PSParser.Transform_scaleContext, 0) + + def transform_swap(self): + return self.getTypedRuleContext(PSParser.Transform_swapContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_elementary_transform + + def enterRule(self, listener): + if hasattr(listener, "enterElementary_transform"): + listener.enterElementary_transform(self) + + def exitRule(self, listener): + if hasattr(listener, "exitElementary_transform"): + listener.exitElementary_transform(self) + + def elementary_transform(self): + + localctx = PSParser.Elementary_transformContext(self, self._ctx, self.state) + self.enterRule(localctx, 14, self.RULE_elementary_transform) + try: + self.state = 160 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 3, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 157 + self.transform_assignment() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 158 + self.transform_scale() + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 159 + self.transform_swap() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Elementary_transformsContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Elementary_transformsContext, self).__init__(parent, invokingState) + self.parser = parser + + def elementary_transform(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Elementary_transformContext) + else: + return self.getTypedRuleContext(PSParser.Elementary_transformContext, i) + + def COMMA(self, i=None): + if i is None: + return self.getTokens(PSParser.COMMA) + else: + return self.getToken(PSParser.COMMA, i) + + def getRuleIndex(self): + return PSParser.RULE_elementary_transforms + + def enterRule(self, listener): + if hasattr(listener, "enterElementary_transforms"): + listener.enterElementary_transforms(self) + + def exitRule(self, listener): + if hasattr(listener, "exitElementary_transforms"): + listener.exitElementary_transforms(self) + + def elementary_transforms(self): + + localctx = PSParser.Elementary_transformsContext(self, self._ctx, self.state) + self.enterRule(localctx, 16, self.RULE_elementary_transforms) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 162 + self.elementary_transform() + self.state = 167 + self._errHandler.sync(self) + _la = self._input.LA(1) + while _la == 171: + self.state = 163 + self.match(PSParser.COMMA) + self.state = 164 + self.elementary_transform() + self.state = 169 + self._errHandler.sync(self) + _la = self._input.LA(1) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class MatrixContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.MatrixContext, self).__init__(parent, invokingState) + self.parser = parser + + def CMD_MATRIX_START(self): + return self.getToken(PSParser.CMD_MATRIX_START, 0) + + def matrix_row(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Matrix_rowContext) + else: + return self.getTypedRuleContext(PSParser.Matrix_rowContext, i) + + def CMD_MATRIX_END(self): + return self.getToken(PSParser.CMD_MATRIX_END, 0) + + def MATRIX_DEL_ROW(self, i=None): + if i is None: + return self.getTokens(PSParser.MATRIX_DEL_ROW) + else: + return self.getToken(PSParser.MATRIX_DEL_ROW, i) + + def MATRIX_XRIGHTARROW(self): + return self.getToken(PSParser.MATRIX_XRIGHTARROW, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def elementary_transforms(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Elementary_transformsContext) + else: + return self.getTypedRuleContext(PSParser.Elementary_transformsContext, i) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def L_BRACKET(self): + return self.getToken(PSParser.L_BRACKET, 0) + + def R_BRACKET(self): + return self.getToken(PSParser.R_BRACKET, 0) + + def getRuleIndex(self): + return PSParser.RULE_matrix + + def enterRule(self, listener): + if hasattr(listener, "enterMatrix"): + listener.enterMatrix(self) + + def exitRule(self, listener): + if hasattr(listener, "exitMatrix"): + listener.exitMatrix(self) + + def matrix(self): + + localctx = PSParser.MatrixContext(self, self._ctx, self.state) + self.enterRule(localctx, 18, self.RULE_matrix) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 170 + self.match(PSParser.CMD_MATRIX_START) + self.state = 171 + self.matrix_row() + self.state = 176 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 5, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + self.state = 172 + self.match(PSParser.MATRIX_DEL_ROW) + self.state = 173 + self.matrix_row() + self.state = 178 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 5, self._ctx) + + self.state = 180 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 166: + self.state = 179 + self.match(PSParser.MATRIX_DEL_ROW) + + self.state = 182 + self.match(PSParser.CMD_MATRIX_END) + self.state = 194 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 8, self._ctx) + if la_ == 1: + self.state = 183 + self.match(PSParser.MATRIX_XRIGHTARROW) + self.state = 188 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 61: + self.state = 184 + self.match(PSParser.L_BRACKET) + self.state = 185 + self.elementary_transforms() + self.state = 186 + self.match(PSParser.R_BRACKET) + + self.state = 190 + self.match(PSParser.L_BRACE) + self.state = 191 + self.elementary_transforms() + self.state = 192 + self.match(PSParser.R_BRACE) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class DetContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.DetContext, self).__init__(parent, invokingState) + self.parser = parser + + def CMD_DET_START(self): + return self.getToken(PSParser.CMD_DET_START, 0) + + def matrix_row(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Matrix_rowContext) + else: + return self.getTypedRuleContext(PSParser.Matrix_rowContext, i) + + def CMD_DET_END(self): + return self.getToken(PSParser.CMD_DET_END, 0) + + def MATRIX_DEL_ROW(self, i=None): + if i is None: + return self.getTokens(PSParser.MATRIX_DEL_ROW) + else: + return self.getToken(PSParser.MATRIX_DEL_ROW, i) + + def getRuleIndex(self): + return PSParser.RULE_det + + def enterRule(self, listener): + if hasattr(listener, "enterDet"): + listener.enterDet(self) + + def exitRule(self, listener): + if hasattr(listener, "exitDet"): + listener.exitDet(self) + + def det(self): + + localctx = PSParser.DetContext(self, self._ctx, self.state) + self.enterRule(localctx, 20, self.RULE_det) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 196 + self.match(PSParser.CMD_DET_START) + self.state = 197 + self.matrix_row() + self.state = 202 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 9, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + self.state = 198 + self.match(PSParser.MATRIX_DEL_ROW) + self.state = 199 + self.matrix_row() + self.state = 204 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 9, self._ctx) + + self.state = 206 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 166: + self.state = 205 + self.match(PSParser.MATRIX_DEL_ROW) + + self.state = 208 + self.match(PSParser.CMD_DET_END) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Matrix_rowContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Matrix_rowContext, self).__init__(parent, invokingState) + self.parser = parser + + def expr(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.ExprContext) + else: + return self.getTypedRuleContext(PSParser.ExprContext, i) + + def MATRIX_DEL_COL(self, i=None): + if i is None: + return self.getTokens(PSParser.MATRIX_DEL_COL) + else: + return self.getToken(PSParser.MATRIX_DEL_COL, i) + + def getRuleIndex(self): + return PSParser.RULE_matrix_row + + def enterRule(self, listener): + if hasattr(listener, "enterMatrix_row"): + listener.enterMatrix_row(self) + + def exitRule(self, listener): + if hasattr(listener, "exitMatrix_row"): + listener.exitMatrix_row(self) + + def matrix_row(self): + + localctx = PSParser.Matrix_rowContext(self, self._ctx, self.state) + self.enterRule(localctx, 22, self.RULE_matrix_row) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 210 + self.expr() + self.state = 215 + self._errHandler.sync(self) + _la = self._input.LA(1) + while _la == 165: + self.state = 211 + self.match(PSParser.MATRIX_DEL_COL) + self.state = 212 + self.expr() + self.state = 217 + self._errHandler.sync(self) + _la = self._input.LA(1) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class RelationContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.RelationContext, self).__init__(parent, invokingState) + self.parser = parser + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def relation(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.RelationContext) + else: + return self.getTypedRuleContext(PSParser.RelationContext, i) + + def IN(self): + return self.getToken(PSParser.IN, 0) + + def ASSIGNMENT(self): + return self.getToken(PSParser.ASSIGNMENT, 0) + + def EQUAL(self): + return self.getToken(PSParser.EQUAL, 0) + + def LT(self): + return self.getToken(PSParser.LT, 0) + + def LTE(self): + return self.getToken(PSParser.LTE, 0) + + def GT(self): + return self.getToken(PSParser.GT, 0) + + def GTE(self): + return self.getToken(PSParser.GTE, 0) + + def UNEQUAL(self): + return self.getToken(PSParser.UNEQUAL, 0) + + def getRuleIndex(self): + return PSParser.RULE_relation + + def enterRule(self, listener): + if hasattr(listener, "enterRelation"): + listener.enterRelation(self) + + def exitRule(self, listener): + if hasattr(listener, "exitRelation"): + listener.exitRelation(self) + + def relation(self, _p=0): + _parentctx = self._ctx + _parentState = self.state + localctx = PSParser.RelationContext(self, self._ctx, _parentState) + _prevctx = localctx + _startState = 24 + self.enterRecursionRule(localctx, 24, self.RULE_relation, _p) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 219 + self.expr() + self._ctx.stop = self._input.LT(-1) + self.state = 226 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 12, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + if self._parseListeners is not None: + self.triggerExitRuleEvent() + _prevctx = localctx + localctx = PSParser.RelationContext(self, _parentctx, _parentState) + self.pushNewRecursionContext(localctx, _startState, self.RULE_relation) + self.state = 221 + if not self.precpred(self._ctx, 2): + from antlr4.error.Errors import FailedPredicateException + raise FailedPredicateException(self, "self.precpred(self._ctx, 2)") + self.state = 222 + _la = self._input.LA(1) + if not((((_la - 181)) & ~0x3f) == 0 and ((1 << (_la - 181)) & 255) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 223 + self.relation(3) + self.state = 228 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 12, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.unrollRecursionContexts(_parentctx) + return localctx + + class Relation_listContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Relation_listContext, self).__init__(parent, invokingState) + self.parser = parser + + def relation_list_content(self): + return self.getTypedRuleContext(PSParser.Relation_list_contentContext, 0) + + def L_BRACKET(self): + return self.getToken(PSParser.L_BRACKET, 0) + + def R_BRACKET(self): + return self.getToken(PSParser.R_BRACKET, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def L_BRACE_VISUAL(self): + return self.getToken(PSParser.L_BRACE_VISUAL, 0) + + def R_BRACE_VISUAL(self): + return self.getToken(PSParser.R_BRACE_VISUAL, 0) + + def L_LEFT(self): + return self.getToken(PSParser.L_LEFT, 0) + + def R_RIGHT(self): + return self.getToken(PSParser.R_RIGHT, 0) + + def ML_LEFT(self): + return self.getToken(PSParser.ML_LEFT, 0) + + def MR_RIGHT(self): + return self.getToken(PSParser.MR_RIGHT, 0) + + def getRuleIndex(self): + return PSParser.RULE_relation_list + + def enterRule(self, listener): + if hasattr(listener, "enterRelation_list"): + listener.enterRelation_list(self) + + def exitRule(self, listener): + if hasattr(listener, "exitRelation_list"): + listener.exitRelation_list(self) + + def relation_list(self): + + localctx = PSParser.Relation_listContext(self, self._ctx, self.state) + self.enterRule(localctx, 26, self.RULE_relation_list) + try: + self.state = 266 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 13, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 229 + self.relation_list_content() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 230 + self.match(PSParser.L_BRACKET) + self.state = 231 + self.relation_list_content() + self.state = 232 + self.match(PSParser.R_BRACKET) + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 234 + self.match(PSParser.L_BRACE) + self.state = 235 + self.relation_list_content() + self.state = 236 + self.match(PSParser.R_BRACE) + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 238 + self.match(PSParser.L_BRACE_VISUAL) + self.state = 239 + self.relation_list_content() + self.state = 240 + self.match(PSParser.R_BRACE_VISUAL) + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 242 + self.match(PSParser.L_LEFT) + self.state = 243 + self.match(PSParser.L_BRACKET) + self.state = 244 + self.relation_list_content() + self.state = 245 + self.match(PSParser.R_RIGHT) + self.state = 246 + self.match(PSParser.R_BRACKET) + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 248 + self.match(PSParser.L_LEFT) + self.state = 249 + self.match(PSParser.L_BRACE_VISUAL) + self.state = 250 + self.relation_list_content() + self.state = 251 + self.match(PSParser.R_RIGHT) + self.state = 252 + self.match(PSParser.R_BRACE_VISUAL) + pass + + elif la_ == 7: + self.enterOuterAlt(localctx, 7) + self.state = 254 + self.match(PSParser.ML_LEFT) + self.state = 255 + self.match(PSParser.L_BRACKET) + self.state = 256 + self.relation_list_content() + self.state = 257 + self.match(PSParser.MR_RIGHT) + self.state = 258 + self.match(PSParser.R_BRACKET) + pass + + elif la_ == 8: + self.enterOuterAlt(localctx, 8) + self.state = 260 + self.match(PSParser.ML_LEFT) + self.state = 261 + self.match(PSParser.L_BRACE_VISUAL) + self.state = 262 + self.relation_list_content() + self.state = 263 + self.match(PSParser.MR_RIGHT) + self.state = 264 + self.match(PSParser.R_BRACE_VISUAL) + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Relation_list_contentContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Relation_list_contentContext, self).__init__(parent, invokingState) + self.parser = parser + + def relation(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.RelationContext) + else: + return self.getTypedRuleContext(PSParser.RelationContext, i) + + def COMMA(self, i=None): + if i is None: + return self.getTokens(PSParser.COMMA) + else: + return self.getToken(PSParser.COMMA, i) + + def SEMICOLON(self, i=None): + if i is None: + return self.getTokens(PSParser.SEMICOLON) + else: + return self.getToken(PSParser.SEMICOLON, i) + + def getRuleIndex(self): + return PSParser.RULE_relation_list_content + + def enterRule(self, listener): + if hasattr(listener, "enterRelation_list_content"): + listener.enterRelation_list_content(self) + + def exitRule(self, listener): + if hasattr(listener, "exitRelation_list_content"): + listener.exitRelation_list_content(self) + + def relation_list_content(self): + + localctx = PSParser.Relation_list_contentContext(self, self._ctx, self.state) + self.enterRule(localctx, 28, self.RULE_relation_list_content) + self._la = 0 # Token type + try: + self.state = 288 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 16, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 268 + self.relation(0) + self.state = 269 + self.match(PSParser.COMMA) + self.state = 270 + self.relation(0) + self.state = 275 + self._errHandler.sync(self) + _la = self._input.LA(1) + while _la == 171: + self.state = 271 + self.match(PSParser.COMMA) + self.state = 272 + self.relation(0) + self.state = 277 + self._errHandler.sync(self) + _la = self._input.LA(1) + + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 278 + self.relation(0) + self.state = 279 + self.match(PSParser.SEMICOLON) + self.state = 280 + self.relation(0) + self.state = 285 + self._errHandler.sync(self) + _la = self._input.LA(1) + while _la == 170: + self.state = 281 + self.match(PSParser.SEMICOLON) + self.state = 282 + self.relation(0) + self.state = 287 + self._errHandler.sync(self) + _la = self._input.LA(1) + + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class EqualityContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.EqualityContext, self).__init__(parent, invokingState) + self.parser = parser + + def expr(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.ExprContext) + else: + return self.getTypedRuleContext(PSParser.ExprContext, i) + + def EQUAL(self): + return self.getToken(PSParser.EQUAL, 0) + + def ASSIGNMENT(self): + return self.getToken(PSParser.ASSIGNMENT, 0) + + def getRuleIndex(self): + return PSParser.RULE_equality + + def enterRule(self, listener): + if hasattr(listener, "enterEquality"): + listener.enterEquality(self) + + def exitRule(self, listener): + if hasattr(listener, "exitEquality"): + listener.exitEquality(self) + + def equality(self): + + localctx = PSParser.EqualityContext(self, self._ctx, self.state) + self.enterRule(localctx, 30, self.RULE_equality) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 290 + self.expr() + self.state = 291 + _la = self._input.LA(1) + if not(_la == 182 or _la == 183): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 292 + self.expr() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class ExprContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.ExprContext, self).__init__(parent, invokingState) + self.parser = parser + + def additive(self): + return self.getTypedRuleContext(PSParser.AdditiveContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_expr + + def enterRule(self, listener): + if hasattr(listener, "enterExpr"): + listener.enterExpr(self) + + def exitRule(self, listener): + if hasattr(listener, "exitExpr"): + listener.exitExpr(self) + + def expr(self): + + localctx = PSParser.ExprContext(self, self._ctx, self.state) + self.enterRule(localctx, 32, self.RULE_expr) + try: + self.enterOuterAlt(localctx, 1) + self.state = 294 + self.additive(0) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class AdditiveContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.AdditiveContext, self).__init__(parent, invokingState) + self.parser = parser + + def mp(self): + return self.getTypedRuleContext(PSParser.MpContext, 0) + + def additive(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.AdditiveContext) + else: + return self.getTypedRuleContext(PSParser.AdditiveContext, i) + + def ADD(self): + return self.getToken(PSParser.ADD, 0) + + def SUB(self): + return self.getToken(PSParser.SUB, 0) + + def getRuleIndex(self): + return PSParser.RULE_additive + + def enterRule(self, listener): + if hasattr(listener, "enterAdditive"): + listener.enterAdditive(self) + + def exitRule(self, listener): + if hasattr(listener, "exitAdditive"): + listener.exitAdditive(self) + + def additive(self, _p=0): + _parentctx = self._ctx + _parentState = self.state + localctx = PSParser.AdditiveContext(self, self._ctx, _parentState) + _prevctx = localctx + _startState = 34 + self.enterRecursionRule(localctx, 34, self.RULE_additive, _p) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 297 + self.mp(0) + self._ctx.stop = self._input.LT(-1) + self.state = 304 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 17, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + if self._parseListeners is not None: + self.triggerExitRuleEvent() + _prevctx = localctx + localctx = PSParser.AdditiveContext(self, _parentctx, _parentState) + self.pushNewRecursionContext(localctx, _startState, self.RULE_additive) + self.state = 299 + if not self.precpred(self._ctx, 2): + from antlr4.error.Errors import FailedPredicateException + raise FailedPredicateException(self, "self.precpred(self._ctx, 2)") + self.state = 300 + _la = self._input.LA(1) + if not(_la == 47 or _la == 48): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 301 + self.additive(3) + self.state = 306 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 17, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.unrollRecursionContexts(_parentctx) + return localctx + + class MpContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.MpContext, self).__init__(parent, invokingState) + self.parser = parser + + def unary(self): + return self.getTypedRuleContext(PSParser.UnaryContext, 0) + + def mp(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.MpContext) + else: + return self.getTypedRuleContext(PSParser.MpContext, i) + + def MUL(self): + return self.getToken(PSParser.MUL, 0) + + def CMD_TIMES(self): + return self.getToken(PSParser.CMD_TIMES, 0) + + def CMD_CDOT(self): + return self.getToken(PSParser.CMD_CDOT, 0) + + def DIV(self): + return self.getToken(PSParser.DIV, 0) + + def CMD_DIV(self): + return self.getToken(PSParser.CMD_DIV, 0) + + def COLON(self): + return self.getToken(PSParser.COLON, 0) + + def CMD_MOD(self): + return self.getToken(PSParser.CMD_MOD, 0) + + def getRuleIndex(self): + return PSParser.RULE_mp + + def enterRule(self, listener): + if hasattr(listener, "enterMp"): + listener.enterMp(self) + + def exitRule(self, listener): + if hasattr(listener, "exitMp"): + listener.exitMp(self) + + def mp(self, _p=0): + _parentctx = self._ctx + _parentState = self.state + localctx = PSParser.MpContext(self, self._ctx, _parentState) + _prevctx = localctx + _startState = 36 + self.enterRecursionRule(localctx, 36, self.RULE_mp, _p) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 308 + self.unary() + self._ctx.stop = self._input.LT(-1) + self.state = 315 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 18, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + if self._parseListeners is not None: + self.triggerExitRuleEvent() + _prevctx = localctx + localctx = PSParser.MpContext(self, _parentctx, _parentState) + self.pushNewRecursionContext(localctx, _startState, self.RULE_mp) + self.state = 310 + if not self.precpred(self._ctx, 2): + from antlr4.error.Errors import FailedPredicateException + raise FailedPredicateException(self, "self.precpred(self._ctx, 2)") + self.state = 311 + _la = self._input.LA(1) + if not(_la == 49 or _la == 50 or (((_la - 147)) & ~0x3f) == 0 and ((1 << (_la - 147)) & 4194375) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 312 + self.mp(3) + self.state = 317 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 18, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.unrollRecursionContexts(_parentctx) + return localctx + + class Mp_nofuncContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Mp_nofuncContext, self).__init__(parent, invokingState) + self.parser = parser + + def unary_nofunc(self): + return self.getTypedRuleContext(PSParser.Unary_nofuncContext, 0) + + def mp_nofunc(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Mp_nofuncContext) + else: + return self.getTypedRuleContext(PSParser.Mp_nofuncContext, i) + + def MUL(self): + return self.getToken(PSParser.MUL, 0) + + def CMD_TIMES(self): + return self.getToken(PSParser.CMD_TIMES, 0) + + def CMD_CDOT(self): + return self.getToken(PSParser.CMD_CDOT, 0) + + def DIV(self): + return self.getToken(PSParser.DIV, 0) + + def CMD_DIV(self): + return self.getToken(PSParser.CMD_DIV, 0) + + def COLON(self): + return self.getToken(PSParser.COLON, 0) + + def CMD_MOD(self): + return self.getToken(PSParser.CMD_MOD, 0) + + def getRuleIndex(self): + return PSParser.RULE_mp_nofunc + + def enterRule(self, listener): + if hasattr(listener, "enterMp_nofunc"): + listener.enterMp_nofunc(self) + + def exitRule(self, listener): + if hasattr(listener, "exitMp_nofunc"): + listener.exitMp_nofunc(self) + + def mp_nofunc(self, _p=0): + _parentctx = self._ctx + _parentState = self.state + localctx = PSParser.Mp_nofuncContext(self, self._ctx, _parentState) + _prevctx = localctx + _startState = 38 + self.enterRecursionRule(localctx, 38, self.RULE_mp_nofunc, _p) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 319 + self.unary_nofunc() + self._ctx.stop = self._input.LT(-1) + self.state = 326 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 19, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + if self._parseListeners is not None: + self.triggerExitRuleEvent() + _prevctx = localctx + localctx = PSParser.Mp_nofuncContext(self, _parentctx, _parentState) + self.pushNewRecursionContext(localctx, _startState, self.RULE_mp_nofunc) + self.state = 321 + if not self.precpred(self._ctx, 2): + from antlr4.error.Errors import FailedPredicateException + raise FailedPredicateException(self, "self.precpred(self._ctx, 2)") + self.state = 322 + _la = self._input.LA(1) + if not(_la == 49 or _la == 50 or (((_la - 147)) & ~0x3f) == 0 and ((1 << (_la - 147)) & 4194375) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 323 + self.mp_nofunc(3) + self.state = 328 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 19, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.unrollRecursionContexts(_parentctx) + return localctx + + class UnaryContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.UnaryContext, self).__init__(parent, invokingState) + self.parser = parser + + def unary(self): + return self.getTypedRuleContext(PSParser.UnaryContext, 0) + + def ADD(self): + return self.getToken(PSParser.ADD, 0) + + def SUB(self): + return self.getToken(PSParser.SUB, 0) + + def postfix(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.PostfixContext) + else: + return self.getTypedRuleContext(PSParser.PostfixContext, i) + + def getRuleIndex(self): + return PSParser.RULE_unary + + def enterRule(self, listener): + if hasattr(listener, "enterUnary"): + listener.enterUnary(self) + + def exitRule(self, listener): + if hasattr(listener, "exitUnary"): + listener.exitUnary(self) + + def unary(self): + + localctx = PSParser.UnaryContext(self, self._ctx, self.state) + self.enterRule(localctx, 40, self.RULE_unary) + self._la = 0 # Token type + try: + self.state = 336 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [47, 48]: + self.enterOuterAlt(localctx, 1) + self.state = 329 + _la = self._input.LA(1) + if not(_la == 47 or _la == 48): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 330 + self.unary() + pass + elif token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 51, 53, 55, 57, 59, 61, 63, 65, 66, 68, 69, 70, 72, 74, 76, 78, 80, 82, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 121, 122, 123, 124, 125, 126, 127, 128, 150, 151, 154, 155, 161, 163, 173, 174, 176, 179, 180, 190, 191, 192, 193, 194]: + self.enterOuterAlt(localctx, 2) + self.state = 332 + self._errHandler.sync(self) + _alt = 1 + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + self.state = 331 + self.postfix() + + else: + raise NoViableAltException(self) + self.state = 334 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 20, self._ctx) + + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Unary_nofuncContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Unary_nofuncContext, self).__init__(parent, invokingState) + self.parser = parser + + def unary_nofunc(self): + return self.getTypedRuleContext(PSParser.Unary_nofuncContext, 0) + + def ADD(self): + return self.getToken(PSParser.ADD, 0) + + def SUB(self): + return self.getToken(PSParser.SUB, 0) + + def postfix(self): + return self.getTypedRuleContext(PSParser.PostfixContext, 0) + + def postfix_nofunc(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Postfix_nofuncContext) + else: + return self.getTypedRuleContext(PSParser.Postfix_nofuncContext, i) + + def getRuleIndex(self): + return PSParser.RULE_unary_nofunc + + def enterRule(self, listener): + if hasattr(listener, "enterUnary_nofunc"): + listener.enterUnary_nofunc(self) + + def exitRule(self, listener): + if hasattr(listener, "exitUnary_nofunc"): + listener.exitUnary_nofunc(self) + + def unary_nofunc(self): + + localctx = PSParser.Unary_nofuncContext(self, self._ctx, self.state) + self.enterRule(localctx, 42, self.RULE_unary_nofunc) + self._la = 0 # Token type + try: + self.state = 347 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [47, 48]: + self.enterOuterAlt(localctx, 1) + self.state = 338 + _la = self._input.LA(1) + if not(_la == 47 or _la == 48): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 339 + self.unary_nofunc() + pass + elif token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 51, 53, 55, 57, 59, 61, 63, 65, 66, 68, 69, 70, 72, 74, 76, 78, 80, 82, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 121, 122, 123, 124, 125, 126, 127, 128, 150, 151, 154, 155, 161, 163, 173, 174, 176, 179, 180, 190, 191, 192, 193, 194]: + self.enterOuterAlt(localctx, 2) + self.state = 340 + self.postfix() + self.state = 344 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 22, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + self.state = 341 + self.postfix_nofunc() + self.state = 346 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 22, self._ctx) + + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class PostfixContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.PostfixContext, self).__init__(parent, invokingState) + self.parser = parser + + def exp(self): + return self.getTypedRuleContext(PSParser.ExpContext, 0) + + def postfix_op(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Postfix_opContext) + else: + return self.getTypedRuleContext(PSParser.Postfix_opContext, i) + + def getRuleIndex(self): + return PSParser.RULE_postfix + + def enterRule(self, listener): + if hasattr(listener, "enterPostfix"): + listener.enterPostfix(self) + + def exitRule(self, listener): + if hasattr(listener, "exitPostfix"): + listener.exitPostfix(self) + + def postfix(self): + + localctx = PSParser.PostfixContext(self, self._ctx, self.state) + self.enterRule(localctx, 44, self.RULE_postfix) + try: + self.enterOuterAlt(localctx, 1) + self.state = 349 + self.exp(0) + self.state = 353 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 24, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + self.state = 350 + self.postfix_op() + self.state = 355 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 24, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Postfix_nofuncContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Postfix_nofuncContext, self).__init__(parent, invokingState) + self.parser = parser + + def exp_nofunc(self): + return self.getTypedRuleContext(PSParser.Exp_nofuncContext, 0) + + def postfix_op(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.Postfix_opContext) + else: + return self.getTypedRuleContext(PSParser.Postfix_opContext, i) + + def getRuleIndex(self): + return PSParser.RULE_postfix_nofunc + + def enterRule(self, listener): + if hasattr(listener, "enterPostfix_nofunc"): + listener.enterPostfix_nofunc(self) + + def exitRule(self, listener): + if hasattr(listener, "exitPostfix_nofunc"): + listener.exitPostfix_nofunc(self) + + def postfix_nofunc(self): + + localctx = PSParser.Postfix_nofuncContext(self, self._ctx, self.state) + self.enterRule(localctx, 46, self.RULE_postfix_nofunc) + try: + self.enterOuterAlt(localctx, 1) + self.state = 356 + self.exp_nofunc(0) + self.state = 360 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 25, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + self.state = 357 + self.postfix_op() + self.state = 362 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 25, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Postfix_opContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Postfix_opContext, self).__init__(parent, invokingState) + self.parser = parser + + def BANG(self): + return self.getToken(PSParser.BANG, 0) + + def eval_at(self): + return self.getTypedRuleContext(PSParser.Eval_atContext, 0) + + def transpose(self): + return self.getTypedRuleContext(PSParser.TransposeContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_postfix_op + + def enterRule(self, listener): + if hasattr(listener, "enterPostfix_op"): + listener.enterPostfix_op(self) + + def exitRule(self, listener): + if hasattr(listener, "exitPostfix_op"): + listener.exitPostfix_op(self) + + def postfix_op(self): + + localctx = PSParser.Postfix_opContext(self, self._ctx, self.state) + self.enterRule(localctx, 48, self.RULE_postfix_op) + try: + self.state = 366 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [189]: + self.enterOuterAlt(localctx, 1) + self.state = 363 + self.match(PSParser.BANG) + pass + elif token in [65]: + self.enterOuterAlt(localctx, 2) + self.state = 364 + self.eval_at() + pass + elif token in [41, 42, 43, 44]: + self.enterOuterAlt(localctx, 3) + self.state = 365 + self.transpose() + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Eval_atContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Eval_atContext, self).__init__(parent, invokingState) + self.parser = parser + + def BAR(self): + return self.getToken(PSParser.BAR, 0) + + def eval_at_sup(self): + return self.getTypedRuleContext(PSParser.Eval_at_supContext, 0) + + def eval_at_sub(self): + return self.getTypedRuleContext(PSParser.Eval_at_subContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_eval_at + + def enterRule(self, listener): + if hasattr(listener, "enterEval_at"): + listener.enterEval_at(self) + + def exitRule(self, listener): + if hasattr(listener, "exitEval_at"): + listener.exitEval_at(self) + + def eval_at(self): + + localctx = PSParser.Eval_atContext(self, self._ctx, self.state) + self.enterRule(localctx, 50, self.RULE_eval_at) + try: + self.enterOuterAlt(localctx, 1) + self.state = 368 + self.match(PSParser.BAR) + self.state = 374 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 27, self._ctx) + if la_ == 1: + self.state = 369 + self.eval_at_sup() + pass + + elif la_ == 2: + self.state = 370 + self.eval_at_sub() + pass + + elif la_ == 3: + self.state = 371 + self.eval_at_sup() + self.state = 372 + self.eval_at_sub() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Eval_at_subContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Eval_at_subContext, self).__init__(parent, invokingState) + self.parser = parser + + def UNDERSCORE(self): + return self.getToken(PSParser.UNDERSCORE, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def equality(self): + return self.getTypedRuleContext(PSParser.EqualityContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_eval_at_sub + + def enterRule(self, listener): + if hasattr(listener, "enterEval_at_sub"): + listener.enterEval_at_sub(self) + + def exitRule(self, listener): + if hasattr(listener, "exitEval_at_sub"): + listener.exitEval_at_sub(self) + + def eval_at_sub(self): + + localctx = PSParser.Eval_at_subContext(self, self._ctx, self.state) + self.enterRule(localctx, 52, self.RULE_eval_at_sub) + try: + self.enterOuterAlt(localctx, 1) + self.state = 376 + self.match(PSParser.UNDERSCORE) + self.state = 377 + self.match(PSParser.L_BRACE) + self.state = 380 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 28, self._ctx) + if la_ == 1: + self.state = 378 + self.expr() + pass + + elif la_ == 2: + self.state = 379 + self.equality() + pass + + self.state = 382 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Eval_at_supContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Eval_at_supContext, self).__init__(parent, invokingState) + self.parser = parser + + def CARET(self): + return self.getToken(PSParser.CARET, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def equality(self): + return self.getTypedRuleContext(PSParser.EqualityContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_eval_at_sup + + def enterRule(self, listener): + if hasattr(listener, "enterEval_at_sup"): + listener.enterEval_at_sup(self) + + def exitRule(self, listener): + if hasattr(listener, "exitEval_at_sup"): + listener.exitEval_at_sup(self) + + def eval_at_sup(self): + + localctx = PSParser.Eval_at_supContext(self, self._ctx, self.state) + self.enterRule(localctx, 54, self.RULE_eval_at_sup) + try: + self.enterOuterAlt(localctx, 1) + self.state = 384 + self.match(PSParser.CARET) + self.state = 385 + self.match(PSParser.L_BRACE) + self.state = 388 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 29, self._ctx) + if la_ == 1: + self.state = 386 + self.expr() + pass + + elif la_ == 2: + self.state = 387 + self.equality() + pass + + self.state = 390 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class ExpContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.ExpContext, self).__init__(parent, invokingState) + self.parser = parser + + def comp(self): + return self.getTypedRuleContext(PSParser.CompContext, 0) + + def exp(self): + return self.getTypedRuleContext(PSParser.ExpContext, 0) + + def CARET(self): + return self.getToken(PSParser.CARET, 0) + + def atom(self): + return self.getTypedRuleContext(PSParser.AtomContext, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def subexpr(self): + return self.getTypedRuleContext(PSParser.SubexprContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_exp + + def enterRule(self, listener): + if hasattr(listener, "enterExp"): + listener.enterExp(self) + + def exitRule(self, listener): + if hasattr(listener, "exitExp"): + listener.exitExp(self) + + def exp(self, _p=0): + _parentctx = self._ctx + _parentState = self.state + localctx = PSParser.ExpContext(self, self._ctx, _parentState) + _prevctx = localctx + _startState = 56 + self.enterRecursionRule(localctx, 56, self.RULE_exp, _p) + try: + self.enterOuterAlt(localctx, 1) + self.state = 393 + self.comp() + self._ctx.stop = self._input.LT(-1) + self.state = 409 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 32, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + if self._parseListeners is not None: + self.triggerExitRuleEvent() + _prevctx = localctx + localctx = PSParser.ExpContext(self, _parentctx, _parentState) + self.pushNewRecursionContext(localctx, _startState, self.RULE_exp) + self.state = 395 + if not self.precpred(self._ctx, 2): + from antlr4.error.Errors import FailedPredicateException + raise FailedPredicateException(self, "self.precpred(self._ctx, 2)") + self.state = 396 + self.match(PSParser.CARET) + self.state = 402 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 154, 173, 176, 179, 180, 190, 191, 192, 193, 194]: + self.state = 397 + self.atom() + pass + elif token in [55]: + self.state = 398 + self.match(PSParser.L_BRACE) + self.state = 399 + self.expr() + self.state = 400 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + self.state = 405 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 31, self._ctx) + if la_ == 1: + self.state = 404 + self.subexpr() + + self.state = 411 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 32, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.unrollRecursionContexts(_parentctx) + return localctx + + class Exp_nofuncContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Exp_nofuncContext, self).__init__(parent, invokingState) + self.parser = parser + + def comp_nofunc(self): + return self.getTypedRuleContext(PSParser.Comp_nofuncContext, 0) + + def exp_nofunc(self): + return self.getTypedRuleContext(PSParser.Exp_nofuncContext, 0) + + def CARET(self): + return self.getToken(PSParser.CARET, 0) + + def atom(self): + return self.getTypedRuleContext(PSParser.AtomContext, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def subexpr(self): + return self.getTypedRuleContext(PSParser.SubexprContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_exp_nofunc + + def enterRule(self, listener): + if hasattr(listener, "enterExp_nofunc"): + listener.enterExp_nofunc(self) + + def exitRule(self, listener): + if hasattr(listener, "exitExp_nofunc"): + listener.exitExp_nofunc(self) + + def exp_nofunc(self, _p=0): + _parentctx = self._ctx + _parentState = self.state + localctx = PSParser.Exp_nofuncContext(self, self._ctx, _parentState) + _prevctx = localctx + _startState = 58 + self.enterRecursionRule(localctx, 58, self.RULE_exp_nofunc, _p) + try: + self.enterOuterAlt(localctx, 1) + self.state = 413 + self.comp_nofunc() + self._ctx.stop = self._input.LT(-1) + self.state = 429 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 35, self._ctx) + while _alt != 2 and _alt != ATN.INVALID_ALT_NUMBER: + if _alt == 1: + if self._parseListeners is not None: + self.triggerExitRuleEvent() + _prevctx = localctx + localctx = PSParser.Exp_nofuncContext(self, _parentctx, _parentState) + self.pushNewRecursionContext(localctx, _startState, self.RULE_exp_nofunc) + self.state = 415 + if not self.precpred(self._ctx, 2): + from antlr4.error.Errors import FailedPredicateException + raise FailedPredicateException(self, "self.precpred(self._ctx, 2)") + self.state = 416 + self.match(PSParser.CARET) + self.state = 422 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 154, 173, 176, 179, 180, 190, 191, 192, 193, 194]: + self.state = 417 + self.atom() + pass + elif token in [55]: + self.state = 418 + self.match(PSParser.L_BRACE) + self.state = 419 + self.expr() + self.state = 420 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + self.state = 425 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 34, self._ctx) + if la_ == 1: + self.state = 424 + self.subexpr() + + self.state = 431 + self._errHandler.sync(self) + _alt = self._interp.adaptivePredict(self._input, 35, self._ctx) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.unrollRecursionContexts(_parentctx) + return localctx + + class CompContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.CompContext, self).__init__(parent, invokingState) + self.parser = parser + + def group(self): + return self.getTypedRuleContext(PSParser.GroupContext, 0) + + def norm_group(self): + return self.getTypedRuleContext(PSParser.Norm_groupContext, 0) + + def abs_group(self): + return self.getTypedRuleContext(PSParser.Abs_groupContext, 0) + + def floor_group(self): + return self.getTypedRuleContext(PSParser.Floor_groupContext, 0) + + def ceil_group(self): + return self.getTypedRuleContext(PSParser.Ceil_groupContext, 0) + + def func(self): + return self.getTypedRuleContext(PSParser.FuncContext, 0) + + def atom(self): + return self.getTypedRuleContext(PSParser.AtomContext, 0) + + def frac(self): + return self.getTypedRuleContext(PSParser.FracContext, 0) + + def binom(self): + return self.getTypedRuleContext(PSParser.BinomContext, 0) + + def matrix(self): + return self.getTypedRuleContext(PSParser.MatrixContext, 0) + + def det(self): + return self.getTypedRuleContext(PSParser.DetContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_comp + + def enterRule(self, listener): + if hasattr(listener, "enterComp"): + listener.enterComp(self) + + def exitRule(self, listener): + if hasattr(listener, "exitComp"): + listener.exitComp(self) + + def comp(self): + + localctx = PSParser.CompContext(self, self._ctx, self.state) + self.enterRule(localctx, 60, self.RULE_comp) + try: + self.state = 443 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 36, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 432 + self.group() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 433 + self.norm_group() + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 434 + self.abs_group() + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 435 + self.floor_group() + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 436 + self.ceil_group() + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 437 + self.func() + pass + + elif la_ == 7: + self.enterOuterAlt(localctx, 7) + self.state = 438 + self.atom() + pass + + elif la_ == 8: + self.enterOuterAlt(localctx, 8) + self.state = 439 + self.frac() + pass + + elif la_ == 9: + self.enterOuterAlt(localctx, 9) + self.state = 440 + self.binom() + pass + + elif la_ == 10: + self.enterOuterAlt(localctx, 10) + self.state = 441 + self.matrix() + pass + + elif la_ == 11: + self.enterOuterAlt(localctx, 11) + self.state = 442 + self.det() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Comp_nofuncContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Comp_nofuncContext, self).__init__(parent, invokingState) + self.parser = parser + + def group(self): + return self.getTypedRuleContext(PSParser.GroupContext, 0) + + def norm_group(self): + return self.getTypedRuleContext(PSParser.Norm_groupContext, 0) + + def abs_group(self): + return self.getTypedRuleContext(PSParser.Abs_groupContext, 0) + + def floor_group(self): + return self.getTypedRuleContext(PSParser.Floor_groupContext, 0) + + def ceil_group(self): + return self.getTypedRuleContext(PSParser.Ceil_groupContext, 0) + + def atom(self): + return self.getTypedRuleContext(PSParser.AtomContext, 0) + + def frac(self): + return self.getTypedRuleContext(PSParser.FracContext, 0) + + def binom(self): + return self.getTypedRuleContext(PSParser.BinomContext, 0) + + def matrix(self): + return self.getTypedRuleContext(PSParser.MatrixContext, 0) + + def det(self): + return self.getTypedRuleContext(PSParser.DetContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_comp_nofunc + + def enterRule(self, listener): + if hasattr(listener, "enterComp_nofunc"): + listener.enterComp_nofunc(self) + + def exitRule(self, listener): + if hasattr(listener, "exitComp_nofunc"): + listener.exitComp_nofunc(self) + + def comp_nofunc(self): + + localctx = PSParser.Comp_nofuncContext(self, self._ctx, self.state) + self.enterRule(localctx, 62, self.RULE_comp_nofunc) + try: + self.state = 455 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 37, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 445 + self.group() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 446 + self.norm_group() + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 447 + self.abs_group() + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 448 + self.floor_group() + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 449 + self.ceil_group() + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 450 + self.atom() + pass + + elif la_ == 7: + self.enterOuterAlt(localctx, 7) + self.state = 451 + self.frac() + pass + + elif la_ == 8: + self.enterOuterAlt(localctx, 8) + self.state = 452 + self.binom() + pass + + elif la_ == 9: + self.enterOuterAlt(localctx, 9) + self.state = 453 + self.matrix() + pass + + elif la_ == 10: + self.enterOuterAlt(localctx, 10) + self.state = 454 + self.det() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class GroupContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.GroupContext, self).__init__(parent, invokingState) + self.parser = parser + + def L_PAREN(self): + return self.getToken(PSParser.L_PAREN, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def R_PAREN(self): + return self.getToken(PSParser.R_PAREN, 0) + + def L_GROUP(self): + return self.getToken(PSParser.L_GROUP, 0) + + def R_GROUP(self): + return self.getToken(PSParser.R_GROUP, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def L_BRACE_VISUAL(self): + return self.getToken(PSParser.L_BRACE_VISUAL, 0) + + def R_BRACE_VISUAL(self): + return self.getToken(PSParser.R_BRACE_VISUAL, 0) + + def L_BRACE_CMD(self): + return self.getToken(PSParser.L_BRACE_CMD, 0) + + def R_BRACE_CMD(self): + return self.getToken(PSParser.R_BRACE_CMD, 0) + + def L_BRACKET(self): + return self.getToken(PSParser.L_BRACKET, 0) + + def R_BRACKET(self): + return self.getToken(PSParser.R_BRACKET, 0) + + def L_BRACK(self): + return self.getToken(PSParser.L_BRACK, 0) + + def R_BRACK(self): + return self.getToken(PSParser.R_BRACK, 0) + + def L_LEFT(self): + return self.getToken(PSParser.L_LEFT, 0) + + def R_RIGHT(self): + return self.getToken(PSParser.R_RIGHT, 0) + + def ML_LEFT(self): + return self.getToken(PSParser.ML_LEFT, 0) + + def MR_RIGHT(self): + return self.getToken(PSParser.MR_RIGHT, 0) + + def getRuleIndex(self): + return PSParser.RULE_group + + def enterRule(self, listener): + if hasattr(listener, "enterGroup"): + listener.enterGroup(self) + + def exitRule(self, listener): + if hasattr(listener, "exitGroup"): + listener.exitGroup(self) + + def group(self): + + localctx = PSParser.GroupContext(self, self._ctx, self.state) + self.enterRule(localctx, 64, self.RULE_group) + try: + self.state = 569 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 38, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 457 + self.match(PSParser.L_PAREN) + self.state = 458 + self.expr() + self.state = 459 + self.match(PSParser.R_PAREN) + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 461 + self.match(PSParser.L_GROUP) + self.state = 462 + self.expr() + self.state = 463 + self.match(PSParser.R_GROUP) + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 465 + self.match(PSParser.L_BRACE) + self.state = 466 + self.expr() + self.state = 467 + self.match(PSParser.R_BRACE) + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 469 + self.match(PSParser.L_BRACE_VISUAL) + self.state = 470 + self.expr() + self.state = 471 + self.match(PSParser.R_BRACE_VISUAL) + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 473 + self.match(PSParser.L_BRACE_CMD) + self.state = 474 + self.expr() + self.state = 475 + self.match(PSParser.R_BRACE_CMD) + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 477 + self.match(PSParser.L_BRACKET) + self.state = 478 + self.expr() + self.state = 479 + self.match(PSParser.R_BRACKET) + pass + + elif la_ == 7: + self.enterOuterAlt(localctx, 7) + self.state = 481 + self.match(PSParser.L_BRACK) + self.state = 482 + self.expr() + self.state = 483 + self.match(PSParser.R_BRACK) + pass + + elif la_ == 8: + self.enterOuterAlt(localctx, 8) + self.state = 485 + self.match(PSParser.L_LEFT) + self.state = 486 + self.match(PSParser.L_PAREN) + self.state = 487 + self.expr() + self.state = 488 + self.match(PSParser.R_RIGHT) + self.state = 489 + self.match(PSParser.R_PAREN) + pass + + elif la_ == 9: + self.enterOuterAlt(localctx, 9) + self.state = 491 + self.match(PSParser.L_LEFT) + self.state = 492 + self.match(PSParser.L_GROUP) + self.state = 493 + self.expr() + self.state = 494 + self.match(PSParser.R_RIGHT) + self.state = 495 + self.match(PSParser.R_GROUP) + pass + + elif la_ == 10: + self.enterOuterAlt(localctx, 10) + self.state = 497 + self.match(PSParser.L_LEFT) + self.state = 498 + self.match(PSParser.L_BRACE) + self.state = 499 + self.expr() + self.state = 500 + self.match(PSParser.R_RIGHT) + self.state = 501 + self.match(PSParser.R_BRACE) + pass + + elif la_ == 11: + self.enterOuterAlt(localctx, 11) + self.state = 503 + self.match(PSParser.L_LEFT) + self.state = 504 + self.match(PSParser.L_BRACE_VISUAL) + self.state = 505 + self.expr() + self.state = 506 + self.match(PSParser.R_RIGHT) + self.state = 507 + self.match(PSParser.R_BRACE_VISUAL) + pass + + elif la_ == 12: + self.enterOuterAlt(localctx, 12) + self.state = 509 + self.match(PSParser.L_LEFT) + self.state = 510 + self.match(PSParser.L_BRACE_CMD) + self.state = 511 + self.expr() + self.state = 512 + self.match(PSParser.R_RIGHT) + self.state = 513 + self.match(PSParser.R_BRACE_CMD) + pass + + elif la_ == 13: + self.enterOuterAlt(localctx, 13) + self.state = 515 + self.match(PSParser.L_LEFT) + self.state = 516 + self.match(PSParser.L_BRACKET) + self.state = 517 + self.expr() + self.state = 518 + self.match(PSParser.R_RIGHT) + self.state = 519 + self.match(PSParser.R_BRACKET) + pass + + elif la_ == 14: + self.enterOuterAlt(localctx, 14) + self.state = 521 + self.match(PSParser.L_LEFT) + self.state = 522 + self.match(PSParser.L_BRACK) + self.state = 523 + self.expr() + self.state = 524 + self.match(PSParser.R_RIGHT) + self.state = 525 + self.match(PSParser.R_BRACK) + pass + + elif la_ == 15: + self.enterOuterAlt(localctx, 15) + self.state = 527 + self.match(PSParser.ML_LEFT) + self.state = 528 + self.match(PSParser.L_PAREN) + self.state = 529 + self.expr() + self.state = 530 + self.match(PSParser.MR_RIGHT) + self.state = 531 + self.match(PSParser.R_PAREN) + pass + + elif la_ == 16: + self.enterOuterAlt(localctx, 16) + self.state = 533 + self.match(PSParser.ML_LEFT) + self.state = 534 + self.match(PSParser.L_GROUP) + self.state = 535 + self.expr() + self.state = 536 + self.match(PSParser.MR_RIGHT) + self.state = 537 + self.match(PSParser.R_GROUP) + pass + + elif la_ == 17: + self.enterOuterAlt(localctx, 17) + self.state = 539 + self.match(PSParser.ML_LEFT) + self.state = 540 + self.match(PSParser.L_BRACE) + self.state = 541 + self.expr() + self.state = 542 + self.match(PSParser.MR_RIGHT) + self.state = 543 + self.match(PSParser.R_BRACE) + pass + + elif la_ == 18: + self.enterOuterAlt(localctx, 18) + self.state = 545 + self.match(PSParser.ML_LEFT) + self.state = 546 + self.match(PSParser.L_BRACE_VISUAL) + self.state = 547 + self.expr() + self.state = 548 + self.match(PSParser.MR_RIGHT) + self.state = 549 + self.match(PSParser.R_BRACE_VISUAL) + pass + + elif la_ == 19: + self.enterOuterAlt(localctx, 19) + self.state = 551 + self.match(PSParser.ML_LEFT) + self.state = 552 + self.match(PSParser.L_BRACE_CMD) + self.state = 553 + self.expr() + self.state = 554 + self.match(PSParser.MR_RIGHT) + self.state = 555 + self.match(PSParser.R_BRACE_CMD) + pass + + elif la_ == 20: + self.enterOuterAlt(localctx, 20) + self.state = 557 + self.match(PSParser.ML_LEFT) + self.state = 558 + self.match(PSParser.L_BRACKET) + self.state = 559 + self.expr() + self.state = 560 + self.match(PSParser.MR_RIGHT) + self.state = 561 + self.match(PSParser.R_BRACKET) + pass + + elif la_ == 21: + self.enterOuterAlt(localctx, 21) + self.state = 563 + self.match(PSParser.ML_LEFT) + self.state = 564 + self.match(PSParser.L_BRACK) + self.state = 565 + self.expr() + self.state = 566 + self.match(PSParser.MR_RIGHT) + self.state = 567 + self.match(PSParser.R_BRACK) + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Norm_groupContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Norm_groupContext, self).__init__(parent, invokingState) + self.parser = parser + + def NORM(self, i=None): + if i is None: + return self.getTokens(PSParser.NORM) + else: + return self.getToken(PSParser.NORM, i) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def L_LEFT(self): + return self.getToken(PSParser.L_LEFT, 0) + + def R_RIGHT(self): + return self.getToken(PSParser.R_RIGHT, 0) + + def ML_LEFT(self): + return self.getToken(PSParser.ML_LEFT, 0) + + def MR_RIGHT(self): + return self.getToken(PSParser.MR_RIGHT, 0) + + def getRuleIndex(self): + return PSParser.RULE_norm_group + + def enterRule(self, listener): + if hasattr(listener, "enterNorm_group"): + listener.enterNorm_group(self) + + def exitRule(self, listener): + if hasattr(listener, "exitNorm_group"): + listener.exitNorm_group(self) + + def norm_group(self): + + localctx = PSParser.Norm_groupContext(self, self._ctx, self.state) + self.enterRule(localctx, 66, self.RULE_norm_group) + try: + self.state = 587 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [69]: + self.enterOuterAlt(localctx, 1) + self.state = 571 + self.match(PSParser.NORM) + self.state = 572 + self.expr() + self.state = 573 + self.match(PSParser.NORM) + pass + elif token in [78]: + self.enterOuterAlt(localctx, 2) + self.state = 575 + self.match(PSParser.L_LEFT) + self.state = 576 + self.match(PSParser.NORM) + self.state = 577 + self.expr() + self.state = 578 + self.match(PSParser.R_RIGHT) + self.state = 579 + self.match(PSParser.NORM) + pass + elif token in [80]: + self.enterOuterAlt(localctx, 3) + self.state = 581 + self.match(PSParser.ML_LEFT) + self.state = 582 + self.match(PSParser.NORM) + self.state = 583 + self.expr() + self.state = 584 + self.match(PSParser.MR_RIGHT) + self.state = 585 + self.match(PSParser.NORM) + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Abs_groupContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Abs_groupContext, self).__init__(parent, invokingState) + self.parser = parser + + def BAR(self, i=None): + if i is None: + return self.getTokens(PSParser.BAR) + else: + return self.getToken(PSParser.BAR, i) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def L_VERT(self): + return self.getToken(PSParser.L_VERT, 0) + + def R_VERT(self): + return self.getToken(PSParser.R_VERT, 0) + + def VERT(self, i=None): + if i is None: + return self.getTokens(PSParser.VERT) + else: + return self.getToken(PSParser.VERT, i) + + def L_LEFT(self): + return self.getToken(PSParser.L_LEFT, 0) + + def R_RIGHT(self): + return self.getToken(PSParser.R_RIGHT, 0) + + def ML_LEFT(self): + return self.getToken(PSParser.ML_LEFT, 0) + + def MR_RIGHT(self): + return self.getToken(PSParser.MR_RIGHT, 0) + + def getRuleIndex(self): + return PSParser.RULE_abs_group + + def enterRule(self, listener): + if hasattr(listener, "enterAbs_group"): + listener.enterAbs_group(self) + + def exitRule(self, listener): + if hasattr(listener, "exitAbs_group"): + listener.exitAbs_group(self) + + def abs_group(self): + + localctx = PSParser.Abs_groupContext(self, self._ctx, self.state) + self.enterRule(localctx, 68, self.RULE_abs_group) + try: + self.state = 637 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 40, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 589 + self.match(PSParser.BAR) + self.state = 590 + self.expr() + self.state = 591 + self.match(PSParser.BAR) + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 593 + self.match(PSParser.L_VERT) + self.state = 594 + self.expr() + self.state = 595 + self.match(PSParser.R_VERT) + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 597 + self.match(PSParser.VERT) + self.state = 598 + self.expr() + self.state = 599 + self.match(PSParser.VERT) + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 601 + self.match(PSParser.L_LEFT) + self.state = 602 + self.match(PSParser.BAR) + self.state = 603 + self.expr() + self.state = 604 + self.match(PSParser.R_RIGHT) + self.state = 605 + self.match(PSParser.BAR) + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 607 + self.match(PSParser.L_LEFT) + self.state = 608 + self.match(PSParser.L_VERT) + self.state = 609 + self.expr() + self.state = 610 + self.match(PSParser.R_RIGHT) + self.state = 611 + self.match(PSParser.R_VERT) + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 613 + self.match(PSParser.L_LEFT) + self.state = 614 + self.match(PSParser.VERT) + self.state = 615 + self.expr() + self.state = 616 + self.match(PSParser.R_RIGHT) + self.state = 617 + self.match(PSParser.VERT) + pass + + elif la_ == 7: + self.enterOuterAlt(localctx, 7) + self.state = 619 + self.match(PSParser.ML_LEFT) + self.state = 620 + self.match(PSParser.BAR) + self.state = 621 + self.expr() + self.state = 622 + self.match(PSParser.MR_RIGHT) + self.state = 623 + self.match(PSParser.BAR) + pass + + elif la_ == 8: + self.enterOuterAlt(localctx, 8) + self.state = 625 + self.match(PSParser.ML_LEFT) + self.state = 626 + self.match(PSParser.L_VERT) + self.state = 627 + self.expr() + self.state = 628 + self.match(PSParser.MR_RIGHT) + self.state = 629 + self.match(PSParser.R_VERT) + pass + + elif la_ == 9: + self.enterOuterAlt(localctx, 9) + self.state = 631 + self.match(PSParser.ML_LEFT) + self.state = 632 + self.match(PSParser.VERT) + self.state = 633 + self.expr() + self.state = 634 + self.match(PSParser.MR_RIGHT) + self.state = 635 + self.match(PSParser.VERT) + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Floor_groupContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Floor_groupContext, self).__init__(parent, invokingState) + self.parser = parser + + def L_FLOOR(self): + return self.getToken(PSParser.L_FLOOR, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def R_FLOOR(self): + return self.getToken(PSParser.R_FLOOR, 0) + + def LL_CORNER(self): + return self.getToken(PSParser.LL_CORNER, 0) + + def LR_CORNER(self): + return self.getToken(PSParser.LR_CORNER, 0) + + def L_LEFT(self): + return self.getToken(PSParser.L_LEFT, 0) + + def R_RIGHT(self): + return self.getToken(PSParser.R_RIGHT, 0) + + def ML_LEFT(self): + return self.getToken(PSParser.ML_LEFT, 0) + + def MR_RIGHT(self): + return self.getToken(PSParser.MR_RIGHT, 0) + + def getRuleIndex(self): + return PSParser.RULE_floor_group + + def enterRule(self, listener): + if hasattr(listener, "enterFloor_group"): + listener.enterFloor_group(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFloor_group"): + listener.exitFloor_group(self) + + def floor_group(self): + + localctx = PSParser.Floor_groupContext(self, self._ctx, self.state) + self.enterRule(localctx, 70, self.RULE_floor_group) + try: + self.state = 671 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 41, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 639 + self.match(PSParser.L_FLOOR) + self.state = 640 + self.expr() + self.state = 641 + self.match(PSParser.R_FLOOR) + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 643 + self.match(PSParser.LL_CORNER) + self.state = 644 + self.expr() + self.state = 645 + self.match(PSParser.LR_CORNER) + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 647 + self.match(PSParser.L_LEFT) + self.state = 648 + self.match(PSParser.L_FLOOR) + self.state = 649 + self.expr() + self.state = 650 + self.match(PSParser.R_RIGHT) + self.state = 651 + self.match(PSParser.R_FLOOR) + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 653 + self.match(PSParser.L_LEFT) + self.state = 654 + self.match(PSParser.LL_CORNER) + self.state = 655 + self.expr() + self.state = 656 + self.match(PSParser.R_RIGHT) + self.state = 657 + self.match(PSParser.LR_CORNER) + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 659 + self.match(PSParser.ML_LEFT) + self.state = 660 + self.match(PSParser.L_FLOOR) + self.state = 661 + self.expr() + self.state = 662 + self.match(PSParser.MR_RIGHT) + self.state = 663 + self.match(PSParser.R_FLOOR) + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 665 + self.match(PSParser.ML_LEFT) + self.state = 666 + self.match(PSParser.LL_CORNER) + self.state = 667 + self.expr() + self.state = 668 + self.match(PSParser.MR_RIGHT) + self.state = 669 + self.match(PSParser.LR_CORNER) + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Ceil_groupContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Ceil_groupContext, self).__init__(parent, invokingState) + self.parser = parser + + def L_CEIL(self): + return self.getToken(PSParser.L_CEIL, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def R_CEIL(self): + return self.getToken(PSParser.R_CEIL, 0) + + def UL_CORNER(self): + return self.getToken(PSParser.UL_CORNER, 0) + + def UR_CORNER(self): + return self.getToken(PSParser.UR_CORNER, 0) + + def L_LEFT(self): + return self.getToken(PSParser.L_LEFT, 0) + + def R_RIGHT(self): + return self.getToken(PSParser.R_RIGHT, 0) + + def ML_LEFT(self): + return self.getToken(PSParser.ML_LEFT, 0) + + def MR_RIGHT(self): + return self.getToken(PSParser.MR_RIGHT, 0) + + def getRuleIndex(self): + return PSParser.RULE_ceil_group + + def enterRule(self, listener): + if hasattr(listener, "enterCeil_group"): + listener.enterCeil_group(self) + + def exitRule(self, listener): + if hasattr(listener, "exitCeil_group"): + listener.exitCeil_group(self) + + def ceil_group(self): + + localctx = PSParser.Ceil_groupContext(self, self._ctx, self.state) + self.enterRule(localctx, 72, self.RULE_ceil_group) + try: + self.state = 705 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 42, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 673 + self.match(PSParser.L_CEIL) + self.state = 674 + self.expr() + self.state = 675 + self.match(PSParser.R_CEIL) + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 677 + self.match(PSParser.UL_CORNER) + self.state = 678 + self.expr() + self.state = 679 + self.match(PSParser.UR_CORNER) + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 681 + self.match(PSParser.L_LEFT) + self.state = 682 + self.match(PSParser.L_CEIL) + self.state = 683 + self.expr() + self.state = 684 + self.match(PSParser.R_RIGHT) + self.state = 685 + self.match(PSParser.R_CEIL) + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 687 + self.match(PSParser.L_LEFT) + self.state = 688 + self.match(PSParser.UL_CORNER) + self.state = 689 + self.expr() + self.state = 690 + self.match(PSParser.R_RIGHT) + self.state = 691 + self.match(PSParser.UR_CORNER) + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 693 + self.match(PSParser.ML_LEFT) + self.state = 694 + self.match(PSParser.L_CEIL) + self.state = 695 + self.expr() + self.state = 696 + self.match(PSParser.MR_RIGHT) + self.state = 697 + self.match(PSParser.R_CEIL) + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 699 + self.match(PSParser.ML_LEFT) + self.state = 700 + self.match(PSParser.UL_CORNER) + self.state = 701 + self.expr() + self.state = 702 + self.match(PSParser.MR_RIGHT) + self.state = 703 + self.match(PSParser.UR_CORNER) + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class AccentContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.AccentContext, self).__init__(parent, invokingState) + self.parser = parser + self.base = None # ExprContext + + def accent_symbol(self): + return self.getTypedRuleContext(PSParser.Accent_symbolContext, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_accent + + def enterRule(self, listener): + if hasattr(listener, "enterAccent"): + listener.enterAccent(self) + + def exitRule(self, listener): + if hasattr(listener, "exitAccent"): + listener.exitAccent(self) + + def accent(self): + + localctx = PSParser.AccentContext(self, self._ctx, self.state) + self.enterRule(localctx, 74, self.RULE_accent) + try: + self.enterOuterAlt(localctx, 1) + self.state = 707 + self.accent_symbol() + self.state = 708 + self.match(PSParser.L_BRACE) + self.state = 709 + localctx.base = self.expr() + self.state = 710 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Atom_expr_no_supexprContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Atom_expr_no_supexprContext, self).__init__(parent, invokingState) + self.parser = parser + + def LETTER_NO_E(self): + return self.getToken(PSParser.LETTER_NO_E, 0) + + def GREEK_CMD(self): + return self.getToken(PSParser.GREEK_CMD, 0) + + def OTHER_SYMBOL_CMD(self): + return self.getToken(PSParser.OTHER_SYMBOL_CMD, 0) + + def accent(self): + return self.getTypedRuleContext(PSParser.AccentContext, 0) + + def subexpr(self): + return self.getTypedRuleContext(PSParser.SubexprContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_atom_expr_no_supexpr + + def enterRule(self, listener): + if hasattr(listener, "enterAtom_expr_no_supexpr"): + listener.enterAtom_expr_no_supexpr(self) + + def exitRule(self, listener): + if hasattr(listener, "exitAtom_expr_no_supexpr"): + listener.exitAtom_expr_no_supexpr(self) + + def atom_expr_no_supexpr(self): + + localctx = PSParser.Atom_expr_no_supexprContext(self, self._ctx, self.state) + self.enterRule(localctx, 76, self.RULE_atom_expr_no_supexpr) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 716 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [176]: + self.state = 712 + self.match(PSParser.LETTER_NO_E) + pass + elif token in [191]: + self.state = 713 + self.match(PSParser.GREEK_CMD) + pass + elif token in [192]: + self.state = 714 + self.match(PSParser.OTHER_SYMBOL_CMD) + pass + elif token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 154]: + self.state = 715 + self.accent() + pass + else: + raise NoViableAltException(self) + + self.state = 719 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 167: + self.state = 718 + self.subexpr() + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Atom_exprContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Atom_exprContext, self).__init__(parent, invokingState) + self.parser = parser + + def LETTER_NO_E(self): + return self.getToken(PSParser.LETTER_NO_E, 0) + + def GREEK_CMD(self): + return self.getToken(PSParser.GREEK_CMD, 0) + + def OTHER_SYMBOL_CMD(self): + return self.getToken(PSParser.OTHER_SYMBOL_CMD, 0) + + def accent(self): + return self.getTypedRuleContext(PSParser.AccentContext, 0) + + def supexpr(self): + return self.getTypedRuleContext(PSParser.SupexprContext, 0) + + def subexpr(self): + return self.getTypedRuleContext(PSParser.SubexprContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_atom_expr + + def enterRule(self, listener): + if hasattr(listener, "enterAtom_expr"): + listener.enterAtom_expr(self) + + def exitRule(self, listener): + if hasattr(listener, "exitAtom_expr"): + listener.exitAtom_expr(self) + + def atom_expr(self): + + localctx = PSParser.Atom_exprContext(self, self._ctx, self.state) + self.enterRule(localctx, 78, self.RULE_atom_expr) + try: + self.enterOuterAlt(localctx, 1) + self.state = 725 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [176]: + self.state = 721 + self.match(PSParser.LETTER_NO_E) + pass + elif token in [191]: + self.state = 722 + self.match(PSParser.GREEK_CMD) + pass + elif token in [192]: + self.state = 723 + self.match(PSParser.OTHER_SYMBOL_CMD) + pass + elif token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 154]: + self.state = 724 + self.accent() + pass + else: + raise NoViableAltException(self) + + self.state = 735 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 46, self._ctx) + if la_ == 1: + self.state = 727 + self.supexpr() + self.state = 728 + self.subexpr() + + elif la_ == 2: + self.state = 730 + self.subexpr() + self.state = 731 + self.supexpr() + + elif la_ == 3: + self.state = 733 + self.subexpr() + + elif la_ == 4: + self.state = 734 + self.supexpr() + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class AtomContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.AtomContext, self).__init__(parent, invokingState) + self.parser = parser + + def atom_expr(self): + return self.getTypedRuleContext(PSParser.Atom_exprContext, 0) + + def SYMBOL(self): + return self.getToken(PSParser.SYMBOL, 0) + + def NUMBER(self): + return self.getToken(PSParser.NUMBER, 0) + + def PERCENT_NUMBER(self): + return self.getToken(PSParser.PERCENT_NUMBER, 0) + + def E_NOTATION(self): + return self.getToken(PSParser.E_NOTATION, 0) + + def DIFFERENTIAL(self): + return self.getToken(PSParser.DIFFERENTIAL, 0) + + def mathit(self): + return self.getTypedRuleContext(PSParser.MathitContext, 0) + + def VARIABLE(self): + return self.getToken(PSParser.VARIABLE, 0) + + def getRuleIndex(self): + return PSParser.RULE_atom + + def enterRule(self, listener): + if hasattr(listener, "enterAtom"): + listener.enterAtom(self) + + def exitRule(self, listener): + if hasattr(listener, "exitAtom"): + listener.exitAtom(self) + + def atom(self): + + localctx = PSParser.AtomContext(self, self._ctx, self.state) + self.enterRule(localctx, 80, self.RULE_atom) + try: + self.state = 745 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 47, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 737 + self.atom_expr() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 738 + self.match(PSParser.SYMBOL) + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 739 + self.match(PSParser.NUMBER) + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 740 + self.match(PSParser.PERCENT_NUMBER) + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 741 + self.match(PSParser.E_NOTATION) + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 742 + self.match(PSParser.DIFFERENTIAL) + pass + + elif la_ == 7: + self.enterOuterAlt(localctx, 7) + self.state = 743 + self.mathit() + pass + + elif la_ == 8: + self.enterOuterAlt(localctx, 8) + self.state = 744 + self.match(PSParser.VARIABLE) + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class MathitContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.MathitContext, self).__init__(parent, invokingState) + self.parser = parser + + def CMD_MATHIT(self): + return self.getToken(PSParser.CMD_MATHIT, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def mathit_text(self): + return self.getTypedRuleContext(PSParser.Mathit_textContext, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def getRuleIndex(self): + return PSParser.RULE_mathit + + def enterRule(self, listener): + if hasattr(listener, "enterMathit"): + listener.enterMathit(self) + + def exitRule(self, listener): + if hasattr(listener, "exitMathit"): + listener.exitMathit(self) + + def mathit(self): + + localctx = PSParser.MathitContext(self, self._ctx, self.state) + self.enterRule(localctx, 82, self.RULE_mathit) + try: + self.enterOuterAlt(localctx, 1) + self.state = 747 + self.match(PSParser.CMD_MATHIT) + self.state = 748 + self.match(PSParser.L_BRACE) + self.state = 749 + self.mathit_text() + self.state = 750 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Mathit_textContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Mathit_textContext, self).__init__(parent, invokingState) + self.parser = parser + + def LETTER_NO_E(self, i=None): + if i is None: + return self.getTokens(PSParser.LETTER_NO_E) + else: + return self.getToken(PSParser.LETTER_NO_E, i) + + def E_NOTATION_E(self, i=None): + if i is None: + return self.getTokens(PSParser.E_NOTATION_E) + else: + return self.getToken(PSParser.E_NOTATION_E, i) + + def EXP_E(self, i=None): + if i is None: + return self.getTokens(PSParser.EXP_E) + else: + return self.getToken(PSParser.EXP_E, i) + + def getRuleIndex(self): + return PSParser.RULE_mathit_text + + def enterRule(self, listener): + if hasattr(listener, "enterMathit_text"): + listener.enterMathit_text(self) + + def exitRule(self, listener): + if hasattr(listener, "exitMathit_text"): + listener.exitMathit_text(self) + + def mathit_text(self): + + localctx = PSParser.Mathit_textContext(self, self._ctx, self.state) + self.enterRule(localctx, 84, self.RULE_mathit_text) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 753 + self._errHandler.sync(self) + _la = self._input.LA(1) + while True: + self.state = 752 + _la = self._input.LA(1) + if not((((_la - 174)) & ~0x3f) == 0 and ((1 << (_la - 174)) & 7) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 755 + self._errHandler.sync(self) + _la = self._input.LA(1) + if not ((((_la - 174)) & ~0x3f) == 0 and ((1 << (_la - 174)) & 7) != 0): + break + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class FracContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.FracContext, self).__init__(parent, invokingState) + self.parser = parser + self.upper = None # ExprContext + self.lower = None # ExprContext + + def CMD_FRAC(self): + return self.getToken(PSParser.CMD_FRAC, 0) + + def L_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.L_BRACE) + else: + return self.getToken(PSParser.L_BRACE, i) + + def R_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.R_BRACE) + else: + return self.getToken(PSParser.R_BRACE, i) + + def expr(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.ExprContext) + else: + return self.getTypedRuleContext(PSParser.ExprContext, i) + + def getRuleIndex(self): + return PSParser.RULE_frac + + def enterRule(self, listener): + if hasattr(listener, "enterFrac"): + listener.enterFrac(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFrac"): + listener.exitFrac(self) + + def frac(self): + + localctx = PSParser.FracContext(self, self._ctx, self.state) + self.enterRule(localctx, 86, self.RULE_frac) + try: + self.enterOuterAlt(localctx, 1) + self.state = 757 + self.match(PSParser.CMD_FRAC) + self.state = 758 + self.match(PSParser.L_BRACE) + self.state = 759 + localctx.upper = self.expr() + self.state = 760 + self.match(PSParser.R_BRACE) + self.state = 761 + self.match(PSParser.L_BRACE) + self.state = 762 + localctx.lower = self.expr() + self.state = 763 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class BinomContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.BinomContext, self).__init__(parent, invokingState) + self.parser = parser + self.upper = None # ExprContext + self.lower = None # ExprContext + + def L_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.L_BRACE) + else: + return self.getToken(PSParser.L_BRACE, i) + + def CMD_CHOOSE(self): + return self.getToken(PSParser.CMD_CHOOSE, 0) + + def R_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.R_BRACE) + else: + return self.getToken(PSParser.R_BRACE, i) + + def expr(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.ExprContext) + else: + return self.getTypedRuleContext(PSParser.ExprContext, i) + + def CMD_BINOM(self): + return self.getToken(PSParser.CMD_BINOM, 0) + + def getRuleIndex(self): + return PSParser.RULE_binom + + def enterRule(self, listener): + if hasattr(listener, "enterBinom"): + listener.enterBinom(self) + + def exitRule(self, listener): + if hasattr(listener, "exitBinom"): + listener.exitBinom(self) + + def binom(self): + + localctx = PSParser.BinomContext(self, self._ctx, self.state) + self.enterRule(localctx, 88, self.RULE_binom) + try: + self.state = 779 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [55]: + self.enterOuterAlt(localctx, 1) + self.state = 765 + self.match(PSParser.L_BRACE) + self.state = 766 + localctx.upper = self.expr() + self.state = 767 + self.match(PSParser.CMD_CHOOSE) + self.state = 768 + localctx.lower = self.expr() + self.state = 769 + self.match(PSParser.R_BRACE) + pass + elif token in [151]: + self.enterOuterAlt(localctx, 2) + self.state = 771 + self.match(PSParser.CMD_BINOM) + self.state = 772 + self.match(PSParser.L_BRACE) + self.state = 773 + localctx.upper = self.expr() + self.state = 774 + self.match(PSParser.R_BRACE) + self.state = 775 + self.match(PSParser.L_BRACE) + self.state = 776 + localctx.lower = self.expr() + self.state = 777 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_normal_functions_single_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_normal_functions_single_argContext, self).__init__(parent, invokingState) + self.parser = parser + + def FUNC_LOG(self): + return self.getToken(PSParser.FUNC_LOG, 0) + + def FUNC_LN(self): + return self.getToken(PSParser.FUNC_LN, 0) + + def FUNC_EXP(self): + return self.getToken(PSParser.FUNC_EXP, 0) + + def FUNC_SIN(self): + return self.getToken(PSParser.FUNC_SIN, 0) + + def FUNC_COS(self): + return self.getToken(PSParser.FUNC_COS, 0) + + def FUNC_TAN(self): + return self.getToken(PSParser.FUNC_TAN, 0) + + def FUNC_CSC(self): + return self.getToken(PSParser.FUNC_CSC, 0) + + def FUNC_SEC(self): + return self.getToken(PSParser.FUNC_SEC, 0) + + def FUNC_COT(self): + return self.getToken(PSParser.FUNC_COT, 0) + + def FUNC_ARCSIN(self): + return self.getToken(PSParser.FUNC_ARCSIN, 0) + + def FUNC_ARCCOS(self): + return self.getToken(PSParser.FUNC_ARCCOS, 0) + + def FUNC_ARCTAN(self): + return self.getToken(PSParser.FUNC_ARCTAN, 0) + + def FUNC_ARCCSC(self): + return self.getToken(PSParser.FUNC_ARCCSC, 0) + + def FUNC_ARCSEC(self): + return self.getToken(PSParser.FUNC_ARCSEC, 0) + + def FUNC_ARCCOT(self): + return self.getToken(PSParser.FUNC_ARCCOT, 0) + + def FUNC_SINH(self): + return self.getToken(PSParser.FUNC_SINH, 0) + + def FUNC_COSH(self): + return self.getToken(PSParser.FUNC_COSH, 0) + + def FUNC_TANH(self): + return self.getToken(PSParser.FUNC_TANH, 0) + + def FUNC_ARSINH(self): + return self.getToken(PSParser.FUNC_ARSINH, 0) + + def FUNC_ARCOSH(self): + return self.getToken(PSParser.FUNC_ARCOSH, 0) + + def FUNC_ARTANH(self): + return self.getToken(PSParser.FUNC_ARTANH, 0) + + def FUNC_ARCSINH(self): + return self.getToken(PSParser.FUNC_ARCSINH, 0) + + def FUNC_ARCCOSH(self): + return self.getToken(PSParser.FUNC_ARCCOSH, 0) + + def FUNC_ARCTANH(self): + return self.getToken(PSParser.FUNC_ARCTANH, 0) + + def FUNC_FLOOR(self): + return self.getToken(PSParser.FUNC_FLOOR, 0) + + def FUNC_CEIL(self): + return self.getToken(PSParser.FUNC_CEIL, 0) + + def FUNC_DET(self): + return self.getToken(PSParser.FUNC_DET, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_normal_functions_single_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_normal_functions_single_arg"): + listener.enterFunc_normal_functions_single_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_normal_functions_single_arg"): + listener.exitFunc_normal_functions_single_arg(self) + + def func_normal_functions_single_arg(self): + + localctx = PSParser.Func_normal_functions_single_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 90, self.RULE_func_normal_functions_single_arg) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 781 + _la = self._input.LA(1) + if not((((_la - 87)) & ~0x3f) == 0 and ((1 << (_la - 87)) & 2611356893183) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_normal_functions_multi_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_normal_functions_multi_argContext, self).__init__(parent, invokingState) + self.parser = parser + + def FUNC_GCD(self): + return self.getToken(PSParser.FUNC_GCD, 0) + + def FUNC_LCM(self): + return self.getToken(PSParser.FUNC_LCM, 0) + + def FUNC_MAX(self): + return self.getToken(PSParser.FUNC_MAX, 0) + + def FUNC_MIN(self): + return self.getToken(PSParser.FUNC_MIN, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_normal_functions_multi_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_normal_functions_multi_arg"): + listener.enterFunc_normal_functions_multi_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_normal_functions_multi_arg"): + listener.exitFunc_normal_functions_multi_arg(self) + + def func_normal_functions_multi_arg(self): + + localctx = PSParser.Func_normal_functions_multi_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 92, self.RULE_func_normal_functions_multi_arg) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 783 + _la = self._input.LA(1) + if not((((_la - 122)) & ~0x3f) == 0 and ((1 << (_la - 122)) & 51) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_operator_names_single_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_operator_names_single_argContext, self).__init__(parent, invokingState) + self.parser = parser + + def FUNC_ARSINH_NAME(self): + return self.getToken(PSParser.FUNC_ARSINH_NAME, 0) + + def FUNC_ARCOSH_NAME(self): + return self.getToken(PSParser.FUNC_ARCOSH_NAME, 0) + + def FUNC_ARTANH_NAME(self): + return self.getToken(PSParser.FUNC_ARTANH_NAME, 0) + + def FUNC_ARCSINH_NAME(self): + return self.getToken(PSParser.FUNC_ARCSINH_NAME, 0) + + def FUNC_ARCCOSH_NAME(self): + return self.getToken(PSParser.FUNC_ARCCOSH_NAME, 0) + + def FUNC_ARCTANH_NAME(self): + return self.getToken(PSParser.FUNC_ARCTANH_NAME, 0) + + def FUNC_FLOOR_NAME(self): + return self.getToken(PSParser.FUNC_FLOOR_NAME, 0) + + def FUNC_CEIL_NAME(self): + return self.getToken(PSParser.FUNC_CEIL_NAME, 0) + + def FUNC_EYE_NAME(self): + return self.getToken(PSParser.FUNC_EYE_NAME, 0) + + def FUNC_RANK_NAME(self): + return self.getToken(PSParser.FUNC_RANK_NAME, 0) + + def FUNC_TRACE_NAME(self): + return self.getToken(PSParser.FUNC_TRACE_NAME, 0) + + def FUNC_RREF_NAME(self): + return self.getToken(PSParser.FUNC_RREF_NAME, 0) + + def FUNC_NULLSPACE_NAME(self): + return self.getToken(PSParser.FUNC_NULLSPACE_NAME, 0) + + def FUNC_DIAGONALIZE_NAME(self): + return self.getToken(PSParser.FUNC_DIAGONALIZE_NAME, 0) + + def FUNC_NORM_NAME(self): + return self.getToken(PSParser.FUNC_NORM_NAME, 0) + + def FUNC_EIGENVALS_NAME(self): + return self.getToken(PSParser.FUNC_EIGENVALS_NAME, 0) + + def FUNC_EIGENVECTORS_NAME(self): + return self.getToken(PSParser.FUNC_EIGENVECTORS_NAME, 0) + + def FUNC_SVD_NAME(self): + return self.getToken(PSParser.FUNC_SVD_NAME, 0) + + def FUNC_COLS_NAME(self): + return self.getToken(PSParser.FUNC_COLS_NAME, 0) + + def FUNC_ROWS_NAME(self): + return self.getToken(PSParser.FUNC_ROWS_NAME, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_operator_names_single_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_operator_names_single_arg"): + listener.enterFunc_operator_names_single_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_operator_names_single_arg"): + listener.exitFunc_operator_names_single_arg(self) + + def func_operator_names_single_arg(self): + + localctx = PSParser.Func_operator_names_single_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 94, self.RULE_func_operator_names_single_arg) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 785 + _la = self._input.LA(1) + if not((((_la - 111)) & ~0x3f) == 0 and ((1 << (_la - 111)) & 66830205759) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_operator_names_multi_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_operator_names_multi_argContext, self).__init__(parent, invokingState) + self.parser = parser + + def FUNC_GCD_NAME(self): + return self.getToken(PSParser.FUNC_GCD_NAME, 0) + + def FUNC_LCM_NAME(self): + return self.getToken(PSParser.FUNC_LCM_NAME, 0) + + def FUNC_ZEROS_NAME(self): + return self.getToken(PSParser.FUNC_ZEROS_NAME, 0) + + def FUNC_ORTHOGONALIZE_NAME(self): + return self.getToken(PSParser.FUNC_ORTHOGONALIZE_NAME, 0) + + def FUNC_ONES_NAME(self): + return self.getToken(PSParser.FUNC_ONES_NAME, 0) + + def FUNC_DIAG_NAME(self): + return self.getToken(PSParser.FUNC_DIAG_NAME, 0) + + def FUNC_HSTACK_NAME(self): + return self.getToken(PSParser.FUNC_HSTACK_NAME, 0) + + def FUNC_VSTACK_NAME(self): + return self.getToken(PSParser.FUNC_VSTACK_NAME, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_operator_names_multi_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_operator_names_multi_arg"): + listener.enterFunc_operator_names_multi_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_operator_names_multi_arg"): + listener.exitFunc_operator_names_multi_arg(self) + + def func_operator_names_multi_arg(self): + + localctx = PSParser.Func_operator_names_multi_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 96, self.RULE_func_operator_names_multi_arg) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 787 + _la = self._input.LA(1) + if not((((_la - 117)) & ~0x3f) == 0 and ((1 << (_la - 117)) & 29515779) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_normal_single_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_normal_single_argContext, self).__init__(parent, invokingState) + self.parser = parser + self.func_operator_name = None # Func_operator_names_single_argContext + + def func_normal_functions_single_arg(self): + return self.getTypedRuleContext(PSParser.Func_normal_functions_single_argContext, 0) + + def CMD_OPERATORNAME(self): + return self.getToken(PSParser.CMD_OPERATORNAME, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def func_operator_names_single_arg(self): + return self.getTypedRuleContext(PSParser.Func_operator_names_single_argContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_normal_single_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_normal_single_arg"): + listener.enterFunc_normal_single_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_normal_single_arg"): + listener.exitFunc_normal_single_arg(self) + + def func_normal_single_arg(self): + + localctx = PSParser.Func_normal_single_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 98, self.RULE_func_normal_single_arg) + try: + self.state = 795 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 124, 125, 128]: + self.enterOuterAlt(localctx, 1) + self.state = 789 + self.func_normal_functions_single_arg() + pass + elif token in [155]: + self.enterOuterAlt(localctx, 2) + self.state = 790 + self.match(PSParser.CMD_OPERATORNAME) + self.state = 791 + self.match(PSParser.L_BRACE) + self.state = 792 + localctx.func_operator_name = self.func_operator_names_single_arg() + self.state = 793 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_normal_multi_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_normal_multi_argContext, self).__init__(parent, invokingState) + self.parser = parser + self.func_operator_name = None # Func_operator_names_multi_argContext + + def func_normal_functions_multi_arg(self): + return self.getTypedRuleContext(PSParser.Func_normal_functions_multi_argContext, 0) + + def CMD_OPERATORNAME(self): + return self.getToken(PSParser.CMD_OPERATORNAME, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def func_operator_names_multi_arg(self): + return self.getTypedRuleContext(PSParser.Func_operator_names_multi_argContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_normal_multi_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_normal_multi_arg"): + listener.enterFunc_normal_multi_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_normal_multi_arg"): + listener.exitFunc_normal_multi_arg(self) + + def func_normal_multi_arg(self): + + localctx = PSParser.Func_normal_multi_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 100, self.RULE_func_normal_multi_arg) + try: + self.state = 803 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [122, 123, 126, 127]: + self.enterOuterAlt(localctx, 1) + self.state = 797 + self.func_normal_functions_multi_arg() + pass + elif token in [155]: + self.enterOuterAlt(localctx, 2) + self.state = 798 + self.match(PSParser.CMD_OPERATORNAME) + self.state = 799 + self.match(PSParser.L_BRACE) + self.state = 800 + localctx.func_operator_name = self.func_operator_names_multi_arg() + self.state = 801 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class FuncContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.FuncContext, self).__init__(parent, invokingState) + self.parser = parser + self.root = None # ExprContext + self.base = None # ExprContext + + def func_normal_single_arg(self): + return self.getTypedRuleContext(PSParser.Func_normal_single_argContext, 0) + + def L_PAREN(self): + return self.getToken(PSParser.L_PAREN, 0) + + def func_single_arg(self): + return self.getTypedRuleContext(PSParser.Func_single_argContext, 0) + + def R_PAREN(self): + return self.getToken(PSParser.R_PAREN, 0) + + def func_single_arg_noparens(self): + return self.getTypedRuleContext(PSParser.Func_single_arg_noparensContext, 0) + + def subexpr(self): + return self.getTypedRuleContext(PSParser.SubexprContext, 0) + + def supexpr(self): + return self.getTypedRuleContext(PSParser.SupexprContext, 0) + + def L_LEFT(self): + return self.getToken(PSParser.L_LEFT, 0) + + def R_RIGHT(self): + return self.getToken(PSParser.R_RIGHT, 0) + + def ML_LEFT(self): + return self.getToken(PSParser.ML_LEFT, 0) + + def MR_RIGHT(self): + return self.getToken(PSParser.MR_RIGHT, 0) + + def func_normal_multi_arg(self): + return self.getTypedRuleContext(PSParser.Func_normal_multi_argContext, 0) + + def func_multi_arg(self): + return self.getTypedRuleContext(PSParser.Func_multi_argContext, 0) + + def func_multi_arg_noparens(self): + return self.getTypedRuleContext(PSParser.Func_multi_arg_noparensContext, 0) + + def atom_expr_no_supexpr(self): + return self.getTypedRuleContext(PSParser.Atom_expr_no_supexprContext, 0) + + def func_common_args(self): + return self.getTypedRuleContext(PSParser.Func_common_argsContext, 0) + + def L_BRACKET(self): + return self.getToken(PSParser.L_BRACKET, 0) + + def R_BRACKET(self): + return self.getToken(PSParser.R_BRACKET, 0) + + def L_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.L_BRACE) + else: + return self.getToken(PSParser.L_BRACE, i) + + def R_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.R_BRACE) + else: + return self.getToken(PSParser.R_BRACE, i) + + def FUNC_INT(self): + return self.getToken(PSParser.FUNC_INT, 0) + + def DIFFERENTIAL(self): + return self.getToken(PSParser.DIFFERENTIAL, 0) + + def frac(self): + return self.getTypedRuleContext(PSParser.FracContext, 0) + + def additive(self): + return self.getTypedRuleContext(PSParser.AdditiveContext, 0) + + def UNDERSCORE(self): + return self.getToken(PSParser.UNDERSCORE, 0) + + def CARET(self): + return self.getToken(PSParser.CARET, 0) + + def FUNC_SQRT(self): + return self.getToken(PSParser.FUNC_SQRT, 0) + + def expr(self, i=None): + if i is None: + return self.getTypedRuleContexts(PSParser.ExprContext) + else: + return self.getTypedRuleContext(PSParser.ExprContext, i) + + def mp(self): + return self.getTypedRuleContext(PSParser.MpContext, 0) + + def FUNC_SUM(self): + return self.getToken(PSParser.FUNC_SUM, 0) + + def FUNC_PROD(self): + return self.getToken(PSParser.FUNC_PROD, 0) + + def subeq(self): + return self.getTypedRuleContext(PSParser.SubeqContext, 0) + + def FUNC_LIM(self): + return self.getToken(PSParser.FUNC_LIM, 0) + + def limit_sub(self): + return self.getTypedRuleContext(PSParser.Limit_subContext, 0) + + def EXP_E(self): + return self.getToken(PSParser.EXP_E, 0) + + def getRuleIndex(self): + return PSParser.RULE_func + + def enterRule(self, listener): + if hasattr(listener, "enterFunc"): + listener.enterFunc(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc"): + listener.exitFunc(self) + + def func(self): + + localctx = PSParser.FuncContext(self, self._ctx, self.state) + self.enterRule(localctx, 102, self.RULE_func) + self._la = 0 # Token type + try: + self.state = 971 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 84, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 805 + self.func_normal_single_arg() + self.state = 818 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 56, self._ctx) + if la_ == 1: + self.state = 807 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 167: + self.state = 806 + self.subexpr() + + self.state = 810 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 168: + self.state = 809 + self.supexpr() + + pass + + elif la_ == 2: + self.state = 813 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 168: + self.state = 812 + self.supexpr() + + self.state = 816 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 167: + self.state = 815 + self.subexpr() + + pass + + self.state = 841 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 61, self._ctx) + if la_ == 1: + self.state = 821 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 78: + self.state = 820 + self.match(PSParser.L_LEFT) + + self.state = 823 + self.match(PSParser.L_PAREN) + self.state = 824 + self.func_single_arg() + self.state = 826 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 79: + self.state = 825 + self.match(PSParser.R_RIGHT) + + self.state = 828 + self.match(PSParser.R_PAREN) + pass + + elif la_ == 2: + self.state = 831 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 80: + self.state = 830 + self.match(PSParser.ML_LEFT) + + self.state = 833 + self.match(PSParser.L_PAREN) + self.state = 834 + self.func_single_arg() + self.state = 836 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 81: + self.state = 835 + self.match(PSParser.MR_RIGHT) + + self.state = 838 + self.match(PSParser.R_PAREN) + pass + + elif la_ == 3: + self.state = 840 + self.func_single_arg_noparens() + pass + + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 843 + self.func_normal_multi_arg() + self.state = 856 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 66, self._ctx) + if la_ == 1: + self.state = 845 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 167: + self.state = 844 + self.subexpr() + + self.state = 848 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 168: + self.state = 847 + self.supexpr() + + pass + + elif la_ == 2: + self.state = 851 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 168: + self.state = 850 + self.supexpr() + + self.state = 854 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 167: + self.state = 853 + self.subexpr() + + pass + + self.state = 879 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 71, self._ctx) + if la_ == 1: + self.state = 859 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 78: + self.state = 858 + self.match(PSParser.L_LEFT) + + self.state = 861 + self.match(PSParser.L_PAREN) + self.state = 862 + self.func_multi_arg() + self.state = 864 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 79: + self.state = 863 + self.match(PSParser.R_RIGHT) + + self.state = 866 + self.match(PSParser.R_PAREN) + pass + + elif la_ == 2: + self.state = 869 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 80: + self.state = 868 + self.match(PSParser.ML_LEFT) + + self.state = 871 + self.match(PSParser.L_PAREN) + self.state = 872 + self.func_multi_arg() + self.state = 874 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 81: + self.state = 873 + self.match(PSParser.MR_RIGHT) + + self.state = 876 + self.match(PSParser.R_PAREN) + pass + + elif la_ == 3: + self.state = 878 + self.func_multi_arg_noparens() + pass + + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 881 + self.atom_expr_no_supexpr() + self.state = 883 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 168: + self.state = 882 + self.supexpr() + + self.state = 886 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 78: + self.state = 885 + self.match(PSParser.L_LEFT) + + self.state = 888 + _la = self._input.LA(1) + if not(_la == 51 or _la == 61): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 889 + self.func_common_args() + self.state = 890 + _la = self._input.LA(1) + if not(_la == 52 or _la == 62): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 892 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 74, self._ctx) + if la_ == 1: + self.state = 891 + self.match(PSParser.R_RIGHT) + + pass + + elif la_ == 4: + self.enterOuterAlt(localctx, 4) + self.state = 894 + self.atom_expr_no_supexpr() + self.state = 896 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 168: + self.state = 895 + self.supexpr() + + self.state = 898 + self.match(PSParser.L_BRACE) + self.state = 900 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 78: + self.state = 899 + self.match(PSParser.L_LEFT) + + self.state = 902 + _la = self._input.LA(1) + if not(_la == 51 or _la == 61): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 903 + self.func_common_args() + self.state = 904 + _la = self._input.LA(1) + if not(_la == 52 or _la == 62): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 906 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 79: + self.state = 905 + self.match(PSParser.R_RIGHT) + + self.state = 908 + self.match(PSParser.R_BRACE) + pass + + elif la_ == 5: + self.enterOuterAlt(localctx, 5) + self.state = 910 + self.match(PSParser.FUNC_INT) + self.state = 931 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 78, self._ctx) + if la_ == 1: + self.state = 911 + self.subexpr() + self.state = 912 + self.supexpr() + + elif la_ == 2: + self.state = 914 + self.supexpr() + self.state = 915 + self.subexpr() + + elif la_ == 3: + self.state = 917 + self.match(PSParser.UNDERSCORE) + self.state = 918 + self.match(PSParser.L_BRACE) + self.state = 919 + self.match(PSParser.R_BRACE) + + self.state = 921 + self.match(PSParser.CARET) + self.state = 922 + self.match(PSParser.L_BRACE) + self.state = 923 + self.match(PSParser.R_BRACE) + + elif la_ == 4: + self.state = 924 + self.match(PSParser.CARET) + self.state = 925 + self.match(PSParser.L_BRACE) + self.state = 926 + self.match(PSParser.R_BRACE) + + self.state = 928 + self.match(PSParser.UNDERSCORE) + self.state = 929 + self.match(PSParser.L_BRACE) + self.state = 930 + self.match(PSParser.R_BRACE) + + self.state = 939 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 80, self._ctx) + if la_ == 1: + self.state = 934 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 79, self._ctx) + if la_ == 1: + self.state = 933 + self.additive(0) + + self.state = 936 + self.match(PSParser.DIFFERENTIAL) + pass + + elif la_ == 2: + self.state = 937 + self.frac() + pass + + elif la_ == 3: + self.state = 938 + self.additive(0) + pass + + pass + + elif la_ == 6: + self.enterOuterAlt(localctx, 6) + self.state = 941 + self.match(PSParser.FUNC_SQRT) + self.state = 946 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 61: + self.state = 942 + self.match(PSParser.L_BRACKET) + self.state = 943 + localctx.root = self.expr() + self.state = 944 + self.match(PSParser.R_BRACKET) + + self.state = 948 + self.match(PSParser.L_BRACE) + self.state = 949 + localctx.base = self.expr() + self.state = 950 + self.match(PSParser.R_BRACE) + pass + + elif la_ == 7: + self.enterOuterAlt(localctx, 7) + self.state = 952 + _la = self._input.LA(1) + if not(_la == 85 or _la == 86): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 959 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [167]: + self.state = 953 + self.subeq() + self.state = 954 + self.supexpr() + pass + elif token in [168]: + self.state = 956 + self.supexpr() + self.state = 957 + self.subeq() + pass + else: + raise NoViableAltException(self) + + self.state = 961 + self.mp(0) + pass + + elif la_ == 8: + self.enterOuterAlt(localctx, 8) + self.state = 963 + self.match(PSParser.FUNC_LIM) + self.state = 964 + self.limit_sub() + self.state = 965 + self.mp(0) + pass + + elif la_ == 9: + self.enterOuterAlt(localctx, 9) + self.state = 967 + self.match(PSParser.EXP_E) + self.state = 969 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 83, self._ctx) + if la_ == 1: + self.state = 968 + self.supexpr() + + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class ArgsContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.ArgsContext, self).__init__(parent, invokingState) + self.parser = parser + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def COMMA(self): + return self.getToken(PSParser.COMMA, 0) + + def args(self): + return self.getTypedRuleContext(PSParser.ArgsContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_args + + def enterRule(self, listener): + if hasattr(listener, "enterArgs"): + listener.enterArgs(self) + + def exitRule(self, listener): + if hasattr(listener, "exitArgs"): + listener.exitArgs(self) + + def args(self): + + localctx = PSParser.ArgsContext(self, self._ctx, self.state) + self.enterRule(localctx, 104, self.RULE_args) + try: + self.state = 978 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 85, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 973 + self.expr() + self.state = 974 + self.match(PSParser.COMMA) + self.state = 975 + self.args() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 977 + self.expr() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_common_argsContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_common_argsContext, self).__init__(parent, invokingState) + self.parser = parser + + def atom(self): + return self.getTypedRuleContext(PSParser.AtomContext, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def COMMA(self): + return self.getToken(PSParser.COMMA, 0) + + def args(self): + return self.getTypedRuleContext(PSParser.ArgsContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_common_args + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_common_args"): + listener.enterFunc_common_args(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_common_args"): + listener.exitFunc_common_args(self) + + def func_common_args(self): + + localctx = PSParser.Func_common_argsContext(self, self._ctx, self.state) + self.enterRule(localctx, 106, self.RULE_func_common_args) + try: + self.state = 988 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 86, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 980 + self.atom() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 981 + self.expr() + self.state = 982 + self.match(PSParser.COMMA) + pass + + elif la_ == 3: + self.enterOuterAlt(localctx, 3) + self.state = 984 + self.expr() + self.state = 985 + self.match(PSParser.COMMA) + self.state = 986 + self.args() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Limit_subContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Limit_subContext, self).__init__(parent, invokingState) + self.parser = parser + + def UNDERSCORE(self): + return self.getToken(PSParser.UNDERSCORE, 0) + + def L_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.L_BRACE) + else: + return self.getToken(PSParser.L_BRACE, i) + + def LIM_APPROACH_SYM(self): + return self.getToken(PSParser.LIM_APPROACH_SYM, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def R_BRACE(self, i=None): + if i is None: + return self.getTokens(PSParser.R_BRACE) + else: + return self.getToken(PSParser.R_BRACE, i) + + def LETTER_NO_E(self): + return self.getToken(PSParser.LETTER_NO_E, 0) + + def GREEK_CMD(self): + return self.getToken(PSParser.GREEK_CMD, 0) + + def OTHER_SYMBOL_CMD(self): + return self.getToken(PSParser.OTHER_SYMBOL_CMD, 0) + + def CARET(self): + return self.getToken(PSParser.CARET, 0) + + def ADD(self): + return self.getToken(PSParser.ADD, 0) + + def SUB(self): + return self.getToken(PSParser.SUB, 0) + + def getRuleIndex(self): + return PSParser.RULE_limit_sub + + def enterRule(self, listener): + if hasattr(listener, "enterLimit_sub"): + listener.enterLimit_sub(self) + + def exitRule(self, listener): + if hasattr(listener, "exitLimit_sub"): + listener.exitLimit_sub(self) + + def limit_sub(self): + + localctx = PSParser.Limit_subContext(self, self._ctx, self.state) + self.enterRule(localctx, 108, self.RULE_limit_sub) + self._la = 0 # Token type + try: + self.enterOuterAlt(localctx, 1) + self.state = 990 + self.match(PSParser.UNDERSCORE) + self.state = 991 + self.match(PSParser.L_BRACE) + self.state = 992 + _la = self._input.LA(1) + if not((((_la - 176)) & ~0x3f) == 0 and ((1 << (_la - 176)) & 98305) != 0): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 993 + self.match(PSParser.LIM_APPROACH_SYM) + self.state = 994 + self.expr() + self.state = 999 + self._errHandler.sync(self) + _la = self._input.LA(1) + if _la == 168: + self.state = 995 + self.match(PSParser.CARET) + self.state = 996 + self.match(PSParser.L_BRACE) + self.state = 997 + _la = self._input.LA(1) + if not(_la == 47 or _la == 48): + self._errHandler.recoverInline(self) + else: + self._errHandler.reportMatch(self) + self.consume() + self.state = 998 + self.match(PSParser.R_BRACE) + + self.state = 1001 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_single_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_single_argContext, self).__init__(parent, invokingState) + self.parser = parser + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_single_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_single_arg"): + listener.enterFunc_single_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_single_arg"): + listener.exitFunc_single_arg(self) + + def func_single_arg(self): + + localctx = PSParser.Func_single_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 110, self.RULE_func_single_arg) + try: + self.enterOuterAlt(localctx, 1) + self.state = 1003 + self.expr() + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_single_arg_noparensContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_single_arg_noparensContext, self).__init__(parent, invokingState) + self.parser = parser + + def mp_nofunc(self): + return self.getTypedRuleContext(PSParser.Mp_nofuncContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_single_arg_noparens + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_single_arg_noparens"): + listener.enterFunc_single_arg_noparens(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_single_arg_noparens"): + listener.exitFunc_single_arg_noparens(self) + + def func_single_arg_noparens(self): + + localctx = PSParser.Func_single_arg_noparensContext(self, self._ctx, self.state) + self.enterRule(localctx, 112, self.RULE_func_single_arg_noparens) + try: + self.enterOuterAlt(localctx, 1) + self.state = 1005 + self.mp_nofunc(0) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_multi_argContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_multi_argContext, self).__init__(parent, invokingState) + self.parser = parser + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def COMMA(self): + return self.getToken(PSParser.COMMA, 0) + + def func_multi_arg(self): + return self.getTypedRuleContext(PSParser.Func_multi_argContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_multi_arg + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_multi_arg"): + listener.enterFunc_multi_arg(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_multi_arg"): + listener.exitFunc_multi_arg(self) + + def func_multi_arg(self): + + localctx = PSParser.Func_multi_argContext(self, self._ctx, self.state) + self.enterRule(localctx, 114, self.RULE_func_multi_arg) + try: + self.state = 1012 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 88, self._ctx) + if la_ == 1: + self.enterOuterAlt(localctx, 1) + self.state = 1007 + self.expr() + pass + + elif la_ == 2: + self.enterOuterAlt(localctx, 2) + self.state = 1008 + self.expr() + self.state = 1009 + self.match(PSParser.COMMA) + self.state = 1010 + self.func_multi_arg() + pass + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class Func_multi_arg_noparensContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.Func_multi_arg_noparensContext, self).__init__(parent, invokingState) + self.parser = parser + + def mp_nofunc(self): + return self.getTypedRuleContext(PSParser.Mp_nofuncContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_func_multi_arg_noparens + + def enterRule(self, listener): + if hasattr(listener, "enterFunc_multi_arg_noparens"): + listener.enterFunc_multi_arg_noparens(self) + + def exitRule(self, listener): + if hasattr(listener, "exitFunc_multi_arg_noparens"): + listener.exitFunc_multi_arg_noparens(self) + + def func_multi_arg_noparens(self): + + localctx = PSParser.Func_multi_arg_noparensContext(self, self._ctx, self.state) + self.enterRule(localctx, 116, self.RULE_func_multi_arg_noparens) + try: + self.enterOuterAlt(localctx, 1) + self.state = 1014 + self.mp_nofunc(0) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class SubexprContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.SubexprContext, self).__init__(parent, invokingState) + self.parser = parser + + def UNDERSCORE(self): + return self.getToken(PSParser.UNDERSCORE, 0) + + def atom(self): + return self.getTypedRuleContext(PSParser.AtomContext, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def args(self): + return self.getTypedRuleContext(PSParser.ArgsContext, 0) + + def getRuleIndex(self): + return PSParser.RULE_subexpr + + def enterRule(self, listener): + if hasattr(listener, "enterSubexpr"): + listener.enterSubexpr(self) + + def exitRule(self, listener): + if hasattr(listener, "exitSubexpr"): + listener.exitSubexpr(self) + + def subexpr(self): + + localctx = PSParser.SubexprContext(self, self._ctx, self.state) + self.enterRule(localctx, 118, self.RULE_subexpr) + try: + self.enterOuterAlt(localctx, 1) + self.state = 1016 + self.match(PSParser.UNDERSCORE) + self.state = 1025 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 154, 173, 176, 179, 180, 190, 191, 192, 193, 194]: + self.state = 1017 + self.atom() + pass + elif token in [55]: + self.state = 1018 + self.match(PSParser.L_BRACE) + self.state = 1021 + self._errHandler.sync(self) + la_ = self._interp.adaptivePredict(self._input, 89, self._ctx) + if la_ == 1: + self.state = 1019 + self.expr() + pass + + elif la_ == 2: + self.state = 1020 + self.args() + pass + + self.state = 1023 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class SupexprContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.SupexprContext, self).__init__(parent, invokingState) + self.parser = parser + + def CARET(self): + return self.getToken(PSParser.CARET, 0) + + def atom(self): + return self.getTypedRuleContext(PSParser.AtomContext, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def expr(self): + return self.getTypedRuleContext(PSParser.ExprContext, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def getRuleIndex(self): + return PSParser.RULE_supexpr + + def enterRule(self, listener): + if hasattr(listener, "enterSupexpr"): + listener.enterSupexpr(self) + + def exitRule(self, listener): + if hasattr(listener, "exitSupexpr"): + listener.exitSupexpr(self) + + def supexpr(self): + + localctx = PSParser.SupexprContext(self, self._ctx, self.state) + self.enterRule(localctx, 120, self.RULE_supexpr) + try: + self.enterOuterAlt(localctx, 1) + self.state = 1027 + self.match(PSParser.CARET) + self.state = 1033 + self._errHandler.sync(self) + token = self._input.LA(1) + if token in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 154, 173, 176, 179, 180, 190, 191, 192, 193, 194]: + self.state = 1028 + self.atom() + pass + elif token in [55]: + self.state = 1029 + self.match(PSParser.L_BRACE) + self.state = 1030 + self.expr() + self.state = 1031 + self.match(PSParser.R_BRACE) + pass + else: + raise NoViableAltException(self) + + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class SubeqContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.SubeqContext, self).__init__(parent, invokingState) + self.parser = parser + + def UNDERSCORE(self): + return self.getToken(PSParser.UNDERSCORE, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def equality(self): + return self.getTypedRuleContext(PSParser.EqualityContext, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def getRuleIndex(self): + return PSParser.RULE_subeq + + def enterRule(self, listener): + if hasattr(listener, "enterSubeq"): + listener.enterSubeq(self) + + def exitRule(self, listener): + if hasattr(listener, "exitSubeq"): + listener.exitSubeq(self) + + def subeq(self): + + localctx = PSParser.SubeqContext(self, self._ctx, self.state) + self.enterRule(localctx, 122, self.RULE_subeq) + try: + self.enterOuterAlt(localctx, 1) + self.state = 1035 + self.match(PSParser.UNDERSCORE) + self.state = 1036 + self.match(PSParser.L_BRACE) + self.state = 1037 + self.equality() + self.state = 1038 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + class SupeqContext(ParserRuleContext): + + def __init__(self, parser, parent=None, invokingState=-1): + super(PSParser.SupeqContext, self).__init__(parent, invokingState) + self.parser = parser + + def UNDERSCORE(self): + return self.getToken(PSParser.UNDERSCORE, 0) + + def L_BRACE(self): + return self.getToken(PSParser.L_BRACE, 0) + + def equality(self): + return self.getTypedRuleContext(PSParser.EqualityContext, 0) + + def R_BRACE(self): + return self.getToken(PSParser.R_BRACE, 0) + + def getRuleIndex(self): + return PSParser.RULE_supeq + + def enterRule(self, listener): + if hasattr(listener, "enterSupeq"): + listener.enterSupeq(self) + + def exitRule(self, listener): + if hasattr(listener, "exitSupeq"): + listener.exitSupeq(self) + + def supeq(self): + + localctx = PSParser.SupeqContext(self, self._ctx, self.state) + self.enterRule(localctx, 124, self.RULE_supeq) + try: + self.enterOuterAlt(localctx, 1) + self.state = 1040 + self.match(PSParser.UNDERSCORE) + self.state = 1041 + self.match(PSParser.L_BRACE) + self.state = 1042 + self.equality() + self.state = 1043 + self.match(PSParser.R_BRACE) + except RecognitionException as re: + localctx.exception = re + self._errHandler.reportError(self, re) + self._errHandler.recover(self, re) + finally: + self.exitRule() + return localctx + + def sempred(self, localctx, ruleIndex, predIndex): + if self._predicates == None: + self._predicates = dict() + self._predicates[12] = self.relation_sempred + self._predicates[17] = self.additive_sempred + self._predicates[18] = self.mp_sempred + self._predicates[19] = self.mp_nofunc_sempred + self._predicates[28] = self.exp_sempred + self._predicates[29] = self.exp_nofunc_sempred + pred = self._predicates.get(ruleIndex, None) + if pred is None: + raise Exception("No predicate with index:" + str(ruleIndex)) + else: + return pred(localctx, predIndex) + + def relation_sempred(self, localctx, predIndex): + if predIndex == 0: + return self.precpred(self._ctx, 2) + + def additive_sempred(self, localctx, predIndex): + if predIndex == 1: + return self.precpred(self._ctx, 2) + + def mp_sempred(self, localctx, predIndex): + if predIndex == 2: + return self.precpred(self._ctx, 2) + + def mp_nofunc_sempred(self, localctx, predIndex): + if predIndex == 3: + return self.precpred(self._ctx, 2) + + def exp_sempred(self, localctx, predIndex): + if predIndex == 4: + return self.precpred(self._ctx, 2) + + def exp_nofunc_sempred(self, localctx, predIndex): + if predIndex == 5: + return self.precpred(self._ctx, 2) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/gen/__init__.py b/Qwen2.5-Eval/evaluation/latex2sympy/gen/__init__.py new file mode 100755 index 0000000..e69de29 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/gen/__init__.py diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/icon.png b/Qwen2.5-Eval/evaluation/latex2sympy/icon.png Binary files differnew file mode 100755 index 0000000..a569624 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/icon.png diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/latex2sympy2.py b/Qwen2.5-Eval/evaluation/latex2sympy/latex2sympy2.py new file mode 100755 index 0000000..859a8c7 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/latex2sympy2.py @@ -0,0 +1,1162 @@ +import sympy +import re +from sympy import matrix_symbols, simplify, factor, expand, apart, expand_trig +from antlr4 import InputStream, CommonTokenStream +from antlr4.error.ErrorListener import ErrorListener + +try: + from gen.PSParser import PSParser + from gen.PSLexer import PSLexer + from gen.PSListener import PSListener +except Exception: + from .gen.PSParser import PSParser + from .gen.PSLexer import PSLexer + from .gen.PSListener import PSListener + +from sympy.printing.str import StrPrinter + +from sympy.parsing.sympy_parser import parse_expr + +import hashlib + +is_real = None + +frac_type = r'\frac' + +variances = {} +var = {} + +VARIABLE_VALUES = {} + + +def set_real(value): + global is_real + is_real = value + + +def set_variances(vars): + global variances + variances = vars + global var + var = {} + for variance in vars: + var[str(variance)] = vars[variance] + + +def latex2sympy(sympy: str, variable_values={}): + # record frac + global frac_type + if sympy.find(r'\frac') != -1: + frac_type = r'\frac' + if sympy.find(r'\dfrac') != -1: + frac_type = r'\dfrac' + if sympy.find(r'\tfrac') != -1: + frac_type = r'\tfrac' + sympy = sympy.replace(r'\dfrac', r'\frac') + sympy = sympy.replace(r'\tfrac', r'\frac') + # Translate Transpose + sympy = sympy.replace(r'\mathrm{T}', 'T', -1) + # Translate Derivative + sympy = sympy.replace(r'\mathrm{d}', 'd', -1).replace(r'{\rm d}', 'd', -1) + # Translate Matrix + sympy = sympy.replace(r'\left[\begin{matrix}', r'\begin{bmatrix}', -1).replace(r'\end{matrix}\right]', r'\end{bmatrix}', -1) + # Translate Permutation + sympy = re.sub(r"\(([a-zA-Z0-9+\-*/\\ ]+?)\)_{([a-zA-Z0-9+\-*/\\ ]+?)}", r"\\frac{(\1)!}{((\1)-(\2))!}", sympy) + # Remove \displaystyle + sympy = sympy.replace(r'\displaystyle', ' ', -1) + # Remove \quad + sympy = sympy.replace(r'\quad', ' ', -1).replace(r'\qquad', ' ', -1).replace(r'~', ' ', -1).replace(r'\,', ' ', -1) + # Remove $ + sympy = sympy.replace(r'$', ' ', -1) + + # variable values + global VARIABLE_VALUES + if len(variable_values) > 0: + VARIABLE_VALUES = variable_values + else: + VARIABLE_VALUES = {} + + # setup listener + matherror = MathErrorListener(sympy) + + # stream input + stream = InputStream(sympy) + lex = PSLexer(stream) + lex.removeErrorListeners() + lex.addErrorListener(matherror) + + tokens = CommonTokenStream(lex) + parser = PSParser(tokens) + + # remove default console error listener + parser.removeErrorListeners() + parser.addErrorListener(matherror) + + # process the input + return_data = None + math = parser.math() + + # if a list + if math.relation_list(): + return_data = [] + + # go over list items + relation_list = math.relation_list().relation_list_content() + for list_item in relation_list.relation(): + expr = convert_relation(list_item) + return_data.append(expr) + + # if not, do default + else: + relation = math.relation() + return_data = convert_relation(relation) + + return return_data + + +class MathErrorListener(ErrorListener): + def __init__(self, src): + super(ErrorListener, self).__init__() + self.src = src + + def syntaxError(self, recog, symbol, line, col, msg, e): + fmt = "%s\n%s\n%s" + marker = "~" * col + "^" + + if msg.startswith("missing"): + err = fmt % (msg, self.src, marker) + elif msg.startswith("no viable"): + err = fmt % ("I expected something else here", self.src, marker) + elif msg.startswith("mismatched"): + names = PSParser.literalNames + expected = [names[i] for i in e.getExpectedTokens() if i < len(names)] + if len(expected) < 10: + expected = " ".join(expected) + err = (fmt % ("I expected one of these: " + expected, + self.src, marker)) + else: + err = (fmt % ("I expected something else here", self.src, marker)) + else: + err = fmt % ("I don't understand this", self.src, marker) + raise Exception(err) + + +def convert_relation(rel): + if rel.expr(): + return convert_expr(rel.expr()) + + lh = convert_relation(rel.relation(0)) + rh = convert_relation(rel.relation(1)) + if rel.LT(): + return sympy.StrictLessThan(lh, rh, evaluate=False) + elif rel.LTE(): + return sympy.LessThan(lh, rh, evaluate=False) + elif rel.GT(): + return sympy.StrictGreaterThan(lh, rh, evaluate=False) + elif rel.GTE(): + return sympy.GreaterThan(lh, rh, evaluate=False) + elif rel.EQUAL(): + return sympy.Eq(lh, rh, evaluate=False) + elif rel.ASSIGNMENT(): + # !Use Global variances + if lh.is_Symbol: + # set value + variances[lh] = rh + var[str(lh)] = rh + return rh + else: + # find the symbols in lh - rh + equation = lh - rh + syms = equation.atoms(sympy.Symbol) + if len(syms) > 0: + # Solve equation + result = [] + for sym in syms: + values = sympy.solve(equation, sym) + for value in values: + result.append(sympy.Eq(sym, value, evaluate=False)) + return result + else: + return sympy.Eq(lh, rh, evaluate=False) + elif rel.IN(): + # !Use Global variances + if hasattr(rh, 'is_Pow') and rh.is_Pow and hasattr(rh.exp, 'is_Mul'): + n = rh.exp.args[0] + m = rh.exp.args[1] + if n in variances: + n = variances[n] + if m in variances: + m = variances[m] + rh = sympy.MatrixSymbol(lh, n, m) + variances[lh] = rh + var[str(lh)] = rh + else: + raise Exception("Don't support this form of definition of matrix symbol.") + return lh + elif rel.UNEQUAL(): + return sympy.Ne(lh, rh, evaluate=False) + + +def convert_expr(expr): + if expr.additive(): + return convert_add(expr.additive()) + + +def convert_elementary_transform(matrix, transform): + if transform.transform_scale(): + transform_scale = transform.transform_scale() + transform_atom = transform_scale.transform_atom() + k = None + num = int(transform_atom.NUMBER().getText()) - 1 + if transform_scale.expr(): + k = convert_expr(transform_scale.expr()) + elif transform_scale.group(): + k = convert_expr(transform_scale.group().expr()) + elif transform_scale.SUB(): + k = -1 + else: + k = 1 + if transform_atom.LETTER_NO_E().getText() == 'r': + matrix = matrix.elementary_row_op(op='n->kn', row=num, k=k) + elif transform_atom.LETTER_NO_E().getText() == 'c': + matrix = matrix.elementary_col_op(op='n->kn', col=num, k=k) + else: + raise Exception('Row and col don\'s match') + + elif transform.transform_swap(): + first_atom = transform.transform_swap().transform_atom()[0] + second_atom = transform.transform_swap().transform_atom()[1] + first_num = int(first_atom.NUMBER().getText()) - 1 + second_num = int(second_atom.NUMBER().getText()) - 1 + if first_atom.LETTER_NO_E().getText() != second_atom.LETTER_NO_E().getText(): + raise Exception('Row and col don\'s match') + elif first_atom.LETTER_NO_E().getText() == 'r': + matrix = matrix.elementary_row_op(op='n<->m', row1=first_num, row2=second_num) + elif first_atom.LETTER_NO_E().getText() == 'c': + matrix = matrix.elementary_col_op(op='n<->m', col1=first_num, col2=second_num) + else: + raise Exception('Row and col don\'s match') + + elif transform.transform_assignment(): + first_atom = transform.transform_assignment().transform_atom() + second_atom = transform.transform_assignment().transform_scale().transform_atom() + transform_scale = transform.transform_assignment().transform_scale() + k = None + if transform_scale.expr(): + k = convert_expr(transform_scale.expr()) + elif transform_scale.group(): + k = convert_expr(transform_scale.group().expr()) + elif transform_scale.SUB(): + k = -1 + else: + k = 1 + first_num = int(first_atom.NUMBER().getText()) - 1 + second_num = int(second_atom.NUMBER().getText()) - 1 + if first_atom.LETTER_NO_E().getText() != second_atom.LETTER_NO_E().getText(): + raise Exception('Row and col don\'s match') + elif first_atom.LETTER_NO_E().getText() == 'r': + matrix = matrix.elementary_row_op(op='n->n+km', k=k, row1=first_num, row2=second_num) + elif first_atom.LETTER_NO_E().getText() == 'c': + matrix = matrix.elementary_col_op(op='n->n+km', k=k, col1=first_num, col2=second_num) + else: + raise Exception('Row and col don\'s match') + + return matrix + + +def convert_matrix(matrix): + # build matrix + row = matrix.matrix_row() + tmp = [] + rows = 0 + mat = None + + for r in row: + tmp.append([]) + for expr in r.expr(): + tmp[rows].append(convert_expr(expr)) + rows = rows + 1 + + mat = sympy.Matrix(tmp) + + if hasattr(matrix, 'MATRIX_XRIGHTARROW') and matrix.MATRIX_XRIGHTARROW(): + transforms_list = matrix.elementary_transforms() + if len(transforms_list) == 1: + for transform in transforms_list[0].elementary_transform(): + mat = convert_elementary_transform(mat, transform) + elif len(transforms_list) == 2: + # firstly transform top of xrightarrow + for transform in transforms_list[1].elementary_transform(): + mat = convert_elementary_transform(mat, transform) + # firstly transform bottom of xrightarrow + for transform in transforms_list[0].elementary_transform(): + mat = convert_elementary_transform(mat, transform) + + return mat + + +def add_flat(lh, rh): + if hasattr(lh, 'is_Add') and lh.is_Add or hasattr(rh, 'is_Add') and rh.is_Add: + args = [] + if hasattr(lh, 'is_Add') and lh.is_Add: + args += list(lh.args) + else: + args += [lh] + if hasattr(rh, 'is_Add') and rh.is_Add: + args = args + list(rh.args) + else: + args += [rh] + return sympy.Add(*args, evaluate=False) + else: + return sympy.Add(lh, rh, evaluate=False) + + +def mat_add_flat(lh, rh): + if hasattr(lh, 'is_MatAdd') and lh.is_MatAdd or hasattr(rh, 'is_MatAdd') and rh.is_MatAdd: + args = [] + if hasattr(lh, 'is_MatAdd') and lh.is_MatAdd: + args += list(lh.args) + else: + args += [lh] + if hasattr(rh, 'is_MatAdd') and rh.is_MatAdd: + args = args + list(rh.args) + else: + args += [rh] + return sympy.MatAdd(*[arg.doit() for arg in args], evaluate=False) + else: + return sympy.MatAdd(lh.doit(), rh.doit(), evaluate=False) + + +def mul_flat(lh, rh): + if hasattr(lh, 'is_Mul') and lh.is_Mul or hasattr(rh, 'is_Mul') and rh.is_Mul: + args = [] + if hasattr(lh, 'is_Mul') and lh.is_Mul: + args += list(lh.args) + else: + args += [lh] + if hasattr(rh, 'is_Mul') and rh.is_Mul: + args = args + list(rh.args) + else: + args += [rh] + return sympy.Mul(*args, evaluate=False) + else: + return sympy.Mul(lh, rh, evaluate=False) + + +def mat_mul_flat(lh, rh): + if hasattr(lh, 'is_MatMul') and lh.is_MatMul or hasattr(rh, 'is_MatMul') and rh.is_MatMul: + args = [] + if hasattr(lh, 'is_MatMul') and lh.is_MatMul: + args += list(lh.args) + else: + args += [lh] + if hasattr(rh, 'is_MatMul') and rh.is_MatMul: + args = args + list(rh.args) + else: + args += [rh] + return sympy.MatMul(*[arg.doit() for arg in args], evaluate=False) + else: + if hasattr(lh, 'doit') and hasattr(rh, 'doit'): + return sympy.MatMul(lh.doit(), rh.doit(), evaluate=False) + elif hasattr(lh, 'doit') and not hasattr(rh, 'doit'): + return sympy.MatMul(lh.doit(), rh, evaluate=False) + elif not hasattr(lh, 'doit') and hasattr(rh, 'doit'): + return sympy.MatMul(lh, rh.doit(), evaluate=False) + else: + return sympy.MatMul(lh, rh, evaluate=False) + + +def convert_add(add): + if add.ADD(): + lh = convert_add(add.additive(0)) + rh = convert_add(add.additive(1)) + + if lh.is_Matrix or rh.is_Matrix: + return mat_add_flat(lh, rh) + else: + return add_flat(lh, rh) + elif add.SUB(): + lh = convert_add(add.additive(0)) + rh = convert_add(add.additive(1)) + + if lh.is_Matrix or rh.is_Matrix: + return mat_add_flat(lh, mat_mul_flat(-1, rh)) + else: + # If we want to force ordering for variables this should be: + # return Sub(lh, rh, evaluate=False) + if not rh.is_Matrix and rh.func.is_Number: + rh = -rh + else: + rh = mul_flat(-1, rh) + return add_flat(lh, rh) + else: + return convert_mp(add.mp()) + + +def convert_mp(mp): + if hasattr(mp, 'mp'): + mp_left = mp.mp(0) + mp_right = mp.mp(1) + else: + mp_left = mp.mp_nofunc(0) + mp_right = mp.mp_nofunc(1) + + if mp.MUL() or mp.CMD_TIMES() or mp.CMD_CDOT(): + lh = convert_mp(mp_left) + rh = convert_mp(mp_right) + + if lh.is_Matrix or rh.is_Matrix: + return mat_mul_flat(lh, rh) + else: + return mul_flat(lh, rh) + elif mp.DIV() or mp.CMD_DIV() or mp.COLON(): + lh = convert_mp(mp_left) + rh = convert_mp(mp_right) + if lh.is_Matrix or rh.is_Matrix: + return sympy.MatMul(lh, sympy.Pow(rh, -1, evaluate=False), evaluate=False) + else: + return sympy.Mul(lh, sympy.Pow(rh, -1, evaluate=False), evaluate=False) + elif mp.CMD_MOD(): + lh = convert_mp(mp_left) + rh = convert_mp(mp_right) + if rh.is_Matrix: + raise Exception("Cannot perform modulo operation with a matrix as an operand") + else: + return sympy.Mod(lh, rh, evaluate=False) + else: + if hasattr(mp, 'unary'): + return convert_unary(mp.unary()) + else: + return convert_unary(mp.unary_nofunc()) + + +def convert_unary(unary): + if hasattr(unary, 'unary'): + nested_unary = unary.unary() + else: + nested_unary = unary.unary_nofunc() + if hasattr(unary, 'postfix_nofunc'): + first = unary.postfix() + tail = unary.postfix_nofunc() + postfix = [first] + tail + else: + postfix = unary.postfix() + + if unary.ADD(): + return convert_unary(nested_unary) + elif unary.SUB(): + tmp_convert_nested_unary = convert_unary(nested_unary) + if tmp_convert_nested_unary.is_Matrix: + return mat_mul_flat(-1, tmp_convert_nested_unary, evaluate=False) + else: + if tmp_convert_nested_unary.func.is_Number: + return -tmp_convert_nested_unary + else: + return mul_flat(-1, tmp_convert_nested_unary) + elif postfix: + return convert_postfix_list(postfix) + + +def convert_postfix_list(arr, i=0): + if i >= len(arr): + raise Exception("Index out of bounds") + + res = convert_postfix(arr[i]) + + if isinstance(res, sympy.Expr) or isinstance(res, sympy.Matrix) or res is sympy.S.EmptySet: + if i == len(arr) - 1: + return res # nothing to multiply by + else: + # multiply by next + rh = convert_postfix_list(arr, i + 1) + + if res.is_Matrix or rh.is_Matrix: + return mat_mul_flat(res, rh) + else: + return mul_flat(res, rh) + elif isinstance(res, tuple) or isinstance(res, list) or isinstance(res, dict): + return res + else: # must be derivative + wrt = res[0] + if i == len(arr) - 1: + raise Exception("Expected expression for derivative") + else: + expr = convert_postfix_list(arr, i + 1) + return sympy.Derivative(expr, wrt) + + +def do_subs(expr, at): + if at.expr(): + at_expr = convert_expr(at.expr()) + syms = at_expr.atoms(sympy.Symbol) + if len(syms) == 0: + return expr + elif len(syms) > 0: + sym = next(iter(syms)) + return expr.subs(sym, at_expr) + elif at.equality(): + lh = convert_expr(at.equality().expr(0)) + rh = convert_expr(at.equality().expr(1)) + return expr.subs(lh, rh) + + +def convert_postfix(postfix): + if hasattr(postfix, 'exp'): + exp_nested = postfix.exp() + else: + exp_nested = postfix.exp_nofunc() + + exp = convert_exp(exp_nested) + for op in postfix.postfix_op(): + if op.BANG(): + if isinstance(exp, list): + raise Exception("Cannot apply postfix to derivative") + exp = sympy.factorial(exp, evaluate=False) + elif op.eval_at(): + ev = op.eval_at() + at_b = None + at_a = None + if ev.eval_at_sup(): + at_b = do_subs(exp, ev.eval_at_sup()) + if ev.eval_at_sub(): + at_a = do_subs(exp, ev.eval_at_sub()) + if at_b is not None and at_a is not None: + exp = add_flat(at_b, mul_flat(at_a, -1)) + elif at_b is not None: + exp = at_b + elif at_a is not None: + exp = at_a + elif op.transpose(): + try: + exp = exp.T + except: + try: + exp = sympy.transpose(exp) + except: + pass + pass + + return exp + + +def convert_exp(exp): + if hasattr(exp, 'exp'): + exp_nested = exp.exp() + else: + exp_nested = exp.exp_nofunc() + + if exp_nested: + base = convert_exp(exp_nested) + if isinstance(base, list): + raise Exception("Cannot raise derivative to power") + if exp.atom(): + exponent = convert_atom(exp.atom()) + elif exp.expr(): + exponent = convert_expr(exp.expr()) + return sympy.Pow(base, exponent, evaluate=False) + else: + if hasattr(exp, 'comp'): + return convert_comp(exp.comp()) + else: + return convert_comp(exp.comp_nofunc()) + + +def convert_comp(comp): + if comp.group(): + return convert_expr(comp.group().expr()) + elif comp.norm_group(): + return convert_expr(comp.norm_group().expr()).norm() + elif comp.abs_group(): + return sympy.Abs(convert_expr(comp.abs_group().expr()), evaluate=False) + elif comp.floor_group(): + return handle_floor(convert_expr(comp.floor_group().expr())) + elif comp.ceil_group(): + return handle_ceil(convert_expr(comp.ceil_group().expr())) + elif comp.atom(): + return convert_atom(comp.atom()) + elif comp.frac(): + return convert_frac(comp.frac()) + elif comp.binom(): + return convert_binom(comp.binom()) + elif comp.matrix(): + return convert_matrix(comp.matrix()) + elif comp.det(): + # !Use Global variances + return convert_matrix(comp.det()).subs(variances).det() + elif comp.func(): + return convert_func(comp.func()) + + +def convert_atom(atom): + if atom.atom_expr(): + atom_expr = atom.atom_expr() + + # find the atom's text + atom_text = '' + if atom_expr.LETTER_NO_E(): + atom_text = atom_expr.LETTER_NO_E().getText() + if atom_text == "I": + return sympy.I + elif atom_expr.GREEK_CMD(): + atom_text = atom_expr.GREEK_CMD().getText()[1:].strip() + elif atom_expr.OTHER_SYMBOL_CMD(): + atom_text = atom_expr.OTHER_SYMBOL_CMD().getText().strip() + elif atom_expr.accent(): + atom_accent = atom_expr.accent() + # get name for accent + name = atom_accent.start.text + # name = atom_accent.start.text[1:] + # exception: check if bar or overline which are treated both as bar + # if name in ["bar", "overline"]: + # name = "bar" + # if name in ["vec", "overrightarrow"]: + # name = "vec" + # if name in ["tilde", "widetilde"]: + # name = "tilde" + # get the base (variable) + base = atom_accent.base.getText() + # set string to base+name + atom_text = name + '{' + base + '}' + + # find atom's subscript, if any + subscript_text = '' + if atom_expr.subexpr(): + subexpr = atom_expr.subexpr() + subscript = None + if subexpr.expr(): # subscript is expr + subscript = subexpr.expr().getText().strip() + elif subexpr.atom(): # subscript is atom + subscript = subexpr.atom().getText().strip() + elif subexpr.args(): # subscript is args + subscript = subexpr.args().getText().strip() + subscript_inner_text = StrPrinter().doprint(subscript) + if len(subscript_inner_text) > 1: + subscript_text = '_{' + subscript_inner_text + '}' + else: + subscript_text = '_' + subscript_inner_text + + # construct the symbol using the text and optional subscript + atom_symbol = sympy.Symbol(atom_text + subscript_text, real=is_real) + # for matrix symbol + matrix_symbol = None + global var + if atom_text + subscript_text in var: + try: + rh = var[atom_text + subscript_text] + shape = sympy.shape(rh) + matrix_symbol = sympy.MatrixSymbol(atom_text + subscript_text, shape[0], shape[1]) + variances[matrix_symbol] = variances[atom_symbol] + except: + pass + + # find the atom's superscript, and return as a Pow if found + if atom_expr.supexpr(): + supexpr = atom_expr.supexpr() + func_pow = None + if supexpr.expr(): + func_pow = convert_expr(supexpr.expr()) + else: + func_pow = convert_atom(supexpr.atom()) + return sympy.Pow(atom_symbol, func_pow, evaluate=False) + + return atom_symbol if not matrix_symbol else matrix_symbol + elif atom.SYMBOL(): + s = atom.SYMBOL().getText().replace("\\$", "").replace("\\%", "") + if s == "\\infty": + return sympy.oo + elif s == '\\pi': + return sympy.pi + elif s == '\\emptyset': + return sympy.S.EmptySet + else: + raise Exception("Unrecognized symbol") + elif atom.NUMBER(): + s = atom.NUMBER().getText().replace(",", "") + try: + sr = sympy.Rational(s) + return sr + except (TypeError, ValueError): + return sympy.Number(s) + elif atom.E_NOTATION(): + s = atom.E_NOTATION().getText().replace(",", "") + try: + sr = sympy.Rational(s) + return sr + except (TypeError, ValueError): + return sympy.Number(s) + elif atom.DIFFERENTIAL(): + var = get_differential_var(atom.DIFFERENTIAL()) + return sympy.Symbol('d' + var.name, real=is_real) + elif atom.mathit(): + text = rule2text(atom.mathit().mathit_text()) + return sympy.Symbol(text, real=is_real) + elif atom.VARIABLE(): + text = atom.VARIABLE().getText() + is_percent = text.endswith("\\%") + trim_amount = 3 if is_percent else 1 + name = text[10:] + name = name[0:len(name) - trim_amount] + + # add hash to distinguish from regular symbols + hash = hashlib.md5(name.encode()).hexdigest() + symbol_name = name + hash + + # replace the variable for already known variable values + if name in VARIABLE_VALUES: + # if a sympy class + if isinstance(VARIABLE_VALUES[name], tuple(sympy.core.all_classes)): + symbol = VARIABLE_VALUES[name] + + # if NOT a sympy class + else: + symbol = parse_expr(str(VARIABLE_VALUES[name])) + else: + symbol = sympy.Symbol(symbol_name, real=is_real) + + if is_percent: + return sympy.Mul(symbol, sympy.Pow(100, -1, evaluate=False), evaluate=False) + + # return the symbol + return symbol + + elif atom.PERCENT_NUMBER(): + text = atom.PERCENT_NUMBER().getText().replace("\\%", "").replace(",", "") + try: + number = sympy.Rational(text) + except (TypeError, ValueError): + number = sympy.Number(text) + percent = sympy.Rational(number, 100) + return percent + + +def rule2text(ctx): + stream = ctx.start.getInputStream() + # starting index of starting token + startIdx = ctx.start.start + # stopping index of stopping token + stopIdx = ctx.stop.stop + + return stream.getText(startIdx, stopIdx) + + +def convert_frac(frac): + diff_op = False + partial_op = False + lower_itv = frac.lower.getSourceInterval() + lower_itv_len = lower_itv[1] - lower_itv[0] + 1 + if (frac.lower.start == frac.lower.stop and + frac.lower.start.type == PSLexer.DIFFERENTIAL): + wrt = get_differential_var_str(frac.lower.start.text) + diff_op = True + elif (lower_itv_len == 2 and + frac.lower.start.type == PSLexer.SYMBOL and + frac.lower.start.text == '\\partial' and + (frac.lower.stop.type == PSLexer.LETTER_NO_E or frac.lower.stop.type == PSLexer.SYMBOL)): + partial_op = True + wrt = frac.lower.stop.text + if frac.lower.stop.type == PSLexer.SYMBOL: + wrt = wrt[1:] + + if diff_op or partial_op: + wrt = sympy.Symbol(wrt, real=is_real) + if (diff_op and frac.upper.start == frac.upper.stop and + frac.upper.start.type == PSLexer.LETTER_NO_E and + frac.upper.start.text == 'd'): + return [wrt] + elif (partial_op and frac.upper.start == frac.upper.stop and + frac.upper.start.type == PSLexer.SYMBOL and + frac.upper.start.text == '\\partial'): + return [wrt] + upper_text = rule2text(frac.upper) + + expr_top = None + if diff_op and upper_text.startswith('d'): + expr_top = latex2sympy(upper_text[1:]) + elif partial_op and frac.upper.start.text == '\\partial': + expr_top = latex2sympy(upper_text[len('\\partial'):]) + if expr_top: + return sympy.Derivative(expr_top, wrt) + + expr_top = convert_expr(frac.upper) + expr_bot = convert_expr(frac.lower) + if expr_top.is_Matrix or expr_bot.is_Matrix: + return sympy.MatMul(expr_top, sympy.Pow(expr_bot, -1, evaluate=False), evaluate=False) + else: + return sympy.Mul(expr_top, sympy.Pow(expr_bot, -1, evaluate=False), evaluate=False) + + +def convert_binom(binom): + expr_top = convert_expr(binom.upper) + expr_bot = convert_expr(binom.lower) + return sympy.binomial(expr_top, expr_bot) + + +def convert_func(func): + if func.func_normal_single_arg(): + if func.L_PAREN(): # function called with parenthesis + arg = convert_func_arg(func.func_single_arg()) + else: + arg = convert_func_arg(func.func_single_arg_noparens()) + + name = func.func_normal_single_arg().start.text[1:] + + # change arc<trig> -> a<trig> + if name in ["arcsin", "arccos", "arctan", "arccsc", "arcsec", + "arccot"]: + name = "a" + name[3:] + expr = getattr(sympy.functions, name)(arg, evaluate=False) + elif name in ["arsinh", "arcosh", "artanh"]: + name = "a" + name[2:] + expr = getattr(sympy.functions, name)(arg, evaluate=False) + elif name in ["arcsinh", "arccosh", "arctanh"]: + name = "a" + name[3:] + expr = getattr(sympy.functions, name)(arg, evaluate=False) + elif name == "operatorname": + operatorname = func.func_normal_single_arg().func_operator_name.getText() + + if operatorname in ["arsinh", "arcosh", "artanh"]: + operatorname = "a" + operatorname[2:] + expr = getattr(sympy.functions, operatorname)(arg, evaluate=False) + elif operatorname in ["arcsinh", "arccosh", "arctanh"]: + operatorname = "a" + operatorname[3:] + expr = getattr(sympy.functions, operatorname)(arg, evaluate=False) + elif operatorname == "floor": + expr = handle_floor(arg) + elif operatorname == "ceil": + expr = handle_ceil(arg) + elif operatorname == 'eye': + expr = sympy.eye(arg) + elif operatorname == 'rank': + expr = sympy.Integer(arg.rank()) + elif operatorname in ['trace', 'tr']: + expr = arg.trace() + elif operatorname == 'rref': + expr = arg.rref()[0] + elif operatorname == 'nullspace': + expr = arg.nullspace() + elif operatorname == 'norm': + expr = arg.norm() + elif operatorname == 'cols': + expr = [arg.col(i) for i in range(arg.cols)] + elif operatorname == 'rows': + expr = [arg.row(i) for i in range(arg.rows)] + elif operatorname in ['eig', 'eigen', 'diagonalize']: + expr = arg.diagonalize() + elif operatorname in ['eigenvals', 'eigenvalues']: + expr = arg.eigenvals() + elif operatorname in ['eigenvects', 'eigenvectors']: + expr = arg.eigenvects() + elif operatorname in ['svd', 'SVD']: + expr = arg.singular_value_decomposition() + elif name in ["log", "ln"]: + if func.subexpr(): + if func.subexpr().atom(): + base = convert_atom(func.subexpr().atom()) + else: + base = convert_expr(func.subexpr().expr()) + elif name == "log": + base = 10 + elif name == "ln": + base = sympy.E + expr = sympy.log(arg, base, evaluate=False) + elif name in ["exp", "exponentialE"]: + expr = sympy.exp(arg) + elif name == "floor": + expr = handle_floor(arg) + elif name == "ceil": + expr = handle_ceil(arg) + elif name == 'det': + expr = arg.det() + + func_pow = None + should_pow = True + if func.supexpr(): + if func.supexpr().expr(): + func_pow = convert_expr(func.supexpr().expr()) + else: + func_pow = convert_atom(func.supexpr().atom()) + + if name in ["sin", "cos", "tan", "csc", "sec", "cot", "sinh", "cosh", "tanh"]: + if func_pow == -1: + name = "a" + name + should_pow = False + expr = getattr(sympy.functions, name)(arg, evaluate=False) + + if func_pow and should_pow: + expr = sympy.Pow(expr, func_pow, evaluate=False) + + return expr + + elif func.func_normal_multi_arg(): + if func.L_PAREN(): # function called with parenthesis + args = func.func_multi_arg().getText().split(",") + else: + args = func.func_multi_arg_noparens().split(",") + + args = list(map(lambda arg: latex2sympy(arg, VARIABLE_VALUES), args)) + name = func.func_normal_multi_arg().start.text[1:] + + if name == "operatorname": + operatorname = func.func_normal_multi_arg().func_operator_name.getText() + if operatorname in ["gcd", "lcm"]: + expr = handle_gcd_lcm(operatorname, args) + elif operatorname == 'zeros': + expr = sympy.zeros(*args) + elif operatorname == 'ones': + expr = sympy.ones(*args) + elif operatorname == 'diag': + expr = sympy.diag(*args) + elif operatorname == 'hstack': + expr = sympy.Matrix.hstack(*args) + elif operatorname == 'vstack': + expr = sympy.Matrix.vstack(*args) + elif operatorname in ['orth', 'ortho', 'orthogonal', 'orthogonalize']: + if len(args) == 1: + arg = args[0] + expr = sympy.matrices.GramSchmidt([arg.col(i) for i in range(arg.cols)], True) + else: + expr = sympy.matrices.GramSchmidt(args, True) + elif name in ["gcd", "lcm"]: + expr = handle_gcd_lcm(name, args) + elif name in ["max", "min"]: + name = name[0].upper() + name[1:] + expr = getattr(sympy.functions, name)(*args, evaluate=False) + + func_pow = None + should_pow = True + if func.supexpr(): + if func.supexpr().expr(): + func_pow = convert_expr(func.supexpr().expr()) + else: + func_pow = convert_atom(func.supexpr().atom()) + + if func_pow and should_pow: + expr = sympy.Pow(expr, func_pow, evaluate=False) + + return expr + elif func.atom_expr_no_supexpr(): + # define a function + f = sympy.Function(func.atom_expr_no_supexpr().getText()) + # args + args = func.func_common_args().getText().split(",") + if args[-1] == '': + args = args[:-1] + args = [latex2sympy(arg, VARIABLE_VALUES) for arg in args] + # supexpr + if func.supexpr(): + if func.supexpr().expr(): + expr = convert_expr(func.supexpr().expr()) + else: + expr = convert_atom(func.supexpr().atom()) + return sympy.Pow(f(*args), expr, evaluate=False) + else: + return f(*args) + elif func.FUNC_INT(): + return handle_integral(func) + elif func.FUNC_SQRT(): + expr = convert_expr(func.base) + if func.root: + r = convert_expr(func.root) + return sympy.Pow(expr, 1 / r, evaluate=False) + else: + return sympy.Pow(expr, sympy.S.Half, evaluate=False) + elif func.FUNC_SUM(): + return handle_sum_or_prod(func, "summation") + elif func.FUNC_PROD(): + return handle_sum_or_prod(func, "product") + elif func.FUNC_LIM(): + return handle_limit(func) + elif func.EXP_E(): + return handle_exp(func) + + +def convert_func_arg(arg): + if hasattr(arg, 'expr'): + return convert_expr(arg.expr()) + else: + return convert_mp(arg.mp_nofunc()) + + +def handle_integral(func): + if func.additive(): + integrand = convert_add(func.additive()) + elif func.frac(): + integrand = convert_frac(func.frac()) + else: + integrand = 1 + + int_var = None + if func.DIFFERENTIAL(): + int_var = get_differential_var(func.DIFFERENTIAL()) + else: + for sym in integrand.atoms(sympy.Symbol): + s = str(sym) + if len(s) > 1 and s[0] == 'd': + if s[1] == '\\': + int_var = sympy.Symbol(s[2:], real=is_real) + else: + int_var = sympy.Symbol(s[1:], real=is_real) + int_sym = sym + if int_var: + integrand = integrand.subs(int_sym, 1) + else: + # Assume dx by default + int_var = sympy.Symbol('x', real=is_real) + + if func.subexpr(): + if func.subexpr().atom(): + lower = convert_atom(func.subexpr().atom()) + else: + lower = convert_expr(func.subexpr().expr()) + if func.supexpr().atom(): + upper = convert_atom(func.supexpr().atom()) + else: + upper = convert_expr(func.supexpr().expr()) + return sympy.Integral(integrand, (int_var, lower, upper)) + else: + return sympy.Integral(integrand, int_var) + + +def handle_sum_or_prod(func, name): + val = convert_mp(func.mp()) + iter_var = convert_expr(func.subeq().equality().expr(0)) + start = convert_expr(func.subeq().equality().expr(1)) + if func.supexpr().expr(): # ^{expr} + end = convert_expr(func.supexpr().expr()) + else: # ^atom + end = convert_atom(func.supexpr().atom()) + + if name == "summation": + return sympy.Sum(val, (iter_var, start, end)) + elif name == "product": + return sympy.Product(val, (iter_var, start, end)) + + +def handle_limit(func): + sub = func.limit_sub() + if sub.LETTER_NO_E(): + var = sympy.Symbol(sub.LETTER_NO_E().getText(), real=is_real) + elif sub.GREEK_CMD(): + var = sympy.Symbol(sub.GREEK_CMD().getText()[1:].strip(), real=is_real) + elif sub.OTHER_SYMBOL_CMD(): + var = sympy.Symbol(sub.OTHER_SYMBOL_CMD().getText().strip(), real=is_real) + else: + var = sympy.Symbol('x', real=is_real) + if sub.SUB(): + direction = "-" + else: + direction = "+" + approaching = convert_expr(sub.expr()) + content = convert_mp(func.mp()) + + return sympy.Limit(content, var, approaching, direction) + + +def handle_exp(func): + if func.supexpr(): + if func.supexpr().expr(): # ^{expr} + exp_arg = convert_expr(func.supexpr().expr()) + else: # ^atom + exp_arg = convert_atom(func.supexpr().atom()) + else: + exp_arg = 1 + return sympy.exp(exp_arg) + + +def handle_gcd_lcm(f, args): + """ + Return the result of gcd() or lcm(), as UnevaluatedExpr + + f: str - name of function ("gcd" or "lcm") + args: List[Expr] - list of function arguments + """ + + args = tuple(map(sympy.nsimplify, args)) + + # gcd() and lcm() don't support evaluate=False + return sympy.UnevaluatedExpr(getattr(sympy, f)(args)) + + +def handle_floor(expr): + """ + Apply floor() then return the floored expression. + + expr: Expr - sympy expression as an argument to floor() + """ + return sympy.functions.floor(expr, evaluate=False) + + +def handle_ceil(expr): + """ + Apply ceil() then return the ceil-ed expression. + + expr: Expr - sympy expression as an argument to ceil() + """ + return sympy.functions.ceiling(expr, evaluate=False) + + +def get_differential_var(d): + text = get_differential_var_str(d.getText()) + return sympy.Symbol(text, real=is_real) + + +def get_differential_var_str(text): + for i in range(1, len(text)): + c = text[i] + if not (c == " " or c == "\r" or c == "\n" or c == "\t"): + idx = i + break + text = text[idx:] + if text[0] == "\\": + text = text[1:] + return text + + +def latex(tex): + global frac_type + result = sympy.latex(tex) + result = result.replace(r'\frac', frac_type, -1).replace(r'\dfrac', frac_type, -1).replace(r'\tfrac', frac_type, -1) + result = result.replace(r'\left[\begin{matrix}', r'\begin{bmatrix}', -1).replace(r'\end{matrix}\right]', r'\end{bmatrix}', -1) + result = result.replace(r'\left', r'', -1).replace(r'\right', r'', -1) + result = result.replace(r' )', r')', -1) + result = result.replace(r'\log', r'\ln', -1) + return result + + +def latex2latex(tex): + result = latex2sympy(tex) + # if result is a list or tuple or dict + if isinstance(result, list) or isinstance(result, tuple) or isinstance(result, dict): + return latex(result) + else: + return latex(simplify(result.subs(variances).doit().doit())) + + +# Set image value +latex2latex('i=I') +latex2latex('j=I') +# set Identity(i) +for i in range(1, 10): + lh = sympy.Symbol(r'\bm{I}_' + str(i), real=False) + lh_m = sympy.MatrixSymbol(r'\bm{I}_' + str(i), i, i) + rh = sympy.Identity(i).as_mutable() + variances[lh] = rh + variances[lh_m] = rh + var[str(lh)] = rh + +if __name__ == '__main__': + # latex2latex(r'A_1=\begin{bmatrix}1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8\end{bmatrix}') + # latex2latex(r'b_1=\begin{bmatrix}1 \\ 2 \\ 3 \\ 4\end{bmatrix}') + # tex = r"(x+2)|_{x=y+1}" + # tex = r"\operatorname{zeros}(3)" + tex = r"\operatorname{rows}(\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix})" + # print("latex2latex:", latex2latex(tex)) + math = latex2sympy(tex) + # math = math.subs(variances) + print("latex:", tex) + # print("var:", variances) + print("raw_math:", math) + # print("math:", latex(math.doit())) + # print("math_type:", type(math.doit())) + # print("shape:", (math.doit()).shape) + print("cal:", latex2latex(tex)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/requirements.in b/Qwen2.5-Eval/evaluation/latex2sympy/requirements.in new file mode 100755 index 0000000..49c5490 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/requirements.in @@ -0,0 +1,2 @@ +sympy +antlr4-python3-runtime diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/requirements.txt b/Qwen2.5-Eval/evaluation/latex2sympy/requirements.txt new file mode 100755 index 0000000..d940f0b --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/requirements.txt @@ -0,0 +1,12 @@ +# +# This file is autogenerated by pip-compile with Python 3.10 +# by the following command: +# +# pip-compile requirements.in +# +antlr4-python3-runtime==4.11.1 + # via -r requirements.in +mpmath==1.3.0 + # via sympy +sympy==1.12 + # via -r requirements.in diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/linalg_equations.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/linalg_equations.py new file mode 100755 index 0000000..fa65ba7 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/linalg_equations.py @@ -0,0 +1,10 @@ +from latex2sympy import process_sympy +import sys +sys.path.append("..") + +# latex = "2\\begin{pmatrix}1&1&1\\\\0&1&1\\\\0&0&1\\end{pmatrix}\\begin{pmatrix}1&1&1\\\\0&1&1\\\\0&0&1\\end{pmatrix}" +latex = "\\frac{a^{2} \\left(3 \\pi - 4 \\sin{\\left(\\pi \\right)} + \\frac{\\sin{\\left(2 \\pi \\right)}}{2}\\right)}{2}" +math = process_sympy(latex) + +print(type(math)) +print("latex: %s to math: %s" % (latex, math)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/linalg_span.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/linalg_span.py new file mode 100755 index 0000000..2839139 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/linalg_span.py @@ -0,0 +1,19 @@ +from latex2sympy import process_sympy +import sys +sys.path.append("..") + +latex = "\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix},\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "[\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix},\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix}]" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "\\left\\{\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix},\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix}\\right\\}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/matrix.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/matrix.py new file mode 100755 index 0000000..9aed3c2 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/matrix.py @@ -0,0 +1,46 @@ +from latex2sympy import process_sympy +from sympy import * +import sys +sys.path.append("..") + +theta = Symbol('theta', real=True) + +latex = "\\begin{matrix}1&2\\\\3&4\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "\\begin{matrix}1&2\\\\3&4\\\\5&6\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "\\begin{matrix}1&2&3\\\\4&5&6\\\\7&8&9\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "\\begin{matrix}x^1&x^2&x^3\\\\y^1&y^2&y^3\\\\z^1&z^2&z^3\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "\\begin{matrix}x\\\\y\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "2\\cdot\\begin{matrix}x\\\\y\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "2\\cdot\\begin{matrix}x\\\\y\\end{matrix} + \\begin{matrix}2\\\\3\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "-2\\begin{matrix}1&2\\\\3&4\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "2\\cdot\\theta\\begin{matrix}x\\\\y\\end{matrix} + \\begin{matrix}2\\\\3\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) + +latex = "\\theta\\begin{matrix}1\\\\3\\end{matrix} - \\begin{matrix}-1\\\\2\\end{matrix}" +math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, math)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/matrix_placeholders.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/matrix_placeholders.py new file mode 100755 index 0000000..79cb672 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/matrix_placeholders.py @@ -0,0 +1,65 @@ +from latex2sympy import process_sympy +from sympy import * +import sys +import hashlib +import time + +sys.path.append("..") + + +M = Matrix([[1, 2], [3, 4]]) +v = Matrix([1, 2]) + +# sub settings +sub_settings_symbols = {} +sub_settings_symbols[Symbol('M' + hashlib.md5('M'.encode()).hexdigest(), real=True)] = M +sub_settings_symbols[Symbol('v' + hashlib.md5('v'.encode()).hexdigest(), real=True)] = v + + +# one parameters +latex = "\\begin{matrix}1&2\\\\3&4\\end{matrix}\\cdot[!v!]" +equation_sympy_check = MatMul(M, Symbol('v' + hashlib.md5('v'.encode()).hexdigest(), real=True)) +equation_sympy_subs_check = MatMul(M, v) +# placeholders +equation_sympy = process_sympy(latex) +print('latex = %s' % latex) +print('equation_sympy = %s' % equation_sympy) +print('equation_sympy_check = %s' % equation_sympy_check) +print('equation_sympy = %s' % (srepr(equation_sympy))) + +equation_sympy_subs = equation_sympy.subs(sub_settings_symbols, evaluate=False) +print('equation_sympy_subs = %s' % equation_sympy_subs) +print('equation_sympy_subs_check = %s' % equation_sympy_subs_check) + + +# two parameters + +# sub settings +print('') +print('============== Two Parameters -> M*v = Matrix*Vector =============') +sub_settings_symbols = {} +sub_settings_symbols[Symbol('M' + hashlib.md5('M'.encode()).hexdigest(), commutative=False)] = M +sub_settings_symbols[Symbol('v' + hashlib.md5('v'.encode()).hexdigest(), commutative=False)] = v + +latex = "[!M!]\\cdot[!v!]" +math_check = Mul(Symbol('M' + hashlib.md5('M'.encode()).hexdigest(), commutative=False), Symbol('v' + hashlib.md5('v'.encode()).hexdigest(), commutative=False)) +# placeholders +equation_sympy = process_sympy(latex) +print(latex) +print(math_check) +print(equation_sympy) +print(srepr(equation_sympy)) + +# performance +t0 = time.time() + +# process_sympy and substitute at the same time +# Only needed for linalg input +placeholder_values = {'M': M, 'v': v} +equation_sympy_subs = process_sympy(latex, variable_values=placeholder_values) + +t1 = time.time() +print('equation with substituted placeholders = %s' % (str(equation_sympy_subs))) +print('time to process to sympy with placeholders = %s s' % (t1 - t0)) +print('') +print('============== Two Parameters -> M*v = Matrix*Vector =============') diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sandbox.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sandbox.py new file mode 100755 index 0000000..2c41100 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sandbox.py @@ -0,0 +1,23 @@ +from sympy import * +from latex2sympy import process_sympy + + +# latex = '\\variable{a}^{\\variable{b}}' +# variables = {'a': process_sympy('658.95998'), 'b': process_sympy('185083.8060')} +# c_ans_expr = process_sympy(latex, variables) +# print(c_ans_expr) +# print(srepr(c_ans_expr)) +# c_ans = c_ans_expr.doit(deep=False).evalf(chop=True) +# print(c_ans) +# print(srepr(c_ans)) + + +# numeric_responses = ['1', '1.0', '-1', '-1.0', '.5', '-.5', '3x10^3', '3E3', '3,000x10^{-3}', '0.5E-1', '\\frac{1}{3}', '(5\\times 3)^3', '\\sin(1)'] +# for latex in numeric_responses: +# parsed = process_sympy(latex) +# print('latex: ', latex) +# print('sympy: ', parsed) +# print('is_number: ', parsed.is_number) +# print('is_Number: ', parsed.is_Number) +# print('srepr: ', srepr(parsed)) +# print('-----------------------------------------------------') diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sandbox_equality.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sandbox_equality.py new file mode 100755 index 0000000..5e3f444 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sandbox_equality.py @@ -0,0 +1,75 @@ +from sympy import * +from latex2sympy import process_sympy + + +# +# Equality Testing +# + +answer_sets = [ + { + 'correct_answer': '(x-y)(x+2y)', + 'student_answers': [ + 'x^2+xy-2y^2', + '(x-y)(x+2y)', + '(x+2y)(x-y)', + '(2\\times y+x)(-y+x)', + '(y\\cdot 2+x)(-y+x)' + ] + }, + { + 'correct_answer': '2\\pi \\variable{r}^2', + 'student_answers': [ + '2\\pi \\variable{r}^2', + '\\pi 2\\variable{r}^2', + '2\\times \\pi \\times \\variable{r}^2', + '2\\pi \\variable{r} \\times \\variable{r}' + ] + }, + { + 'correct_answer': '2x - 3y', + 'student_answers': [ + '-3y + 2x' + ] + }, + { + 'correct_answer': 'x\\times x', + 'student_answers': [ + 'x\\times x', + 'x\\cdot x', + 'x^2', + '(\\sqrt{x})^{4}' + ] + }, + { + 'correct_answer': '23e^{-1\\times \\sqrt{t^2}}', + 'student_answers': [ + '23e^{-t}' + ] + }, + { + 'correct_answer': 'a=x^2+1', + 'student_answers': [ + 'x^2+1=a' + ] + } +] + +for answer_set in answer_sets: + correct_answer = answer_set['correct_answer'] + correct_answer_parsed = process_sympy(answer_set['correct_answer']) + for student_answer in answer_set['student_answers']: + student_answer_parsed = process_sympy(student_answer) + print('correct_answer (c): ', correct_answer, correct_answer_parsed) + print('student_answer (a): ', student_answer, student_answer_parsed) + print('') + print('Expression Tree (srepr(c) == srepr(a)) =>', srepr(correct_answer_parsed) == srepr(student_answer_parsed)) + print('srepr(c) =>', srepr(correct_answer_parsed)) + print('srepr(a) =>', srepr(student_answer_parsed)) + print('') + # print('Structural (c == a) =>', correct_answer_parsed == student_answer_parsed) + print('Symbolic (simplify(c - s) == 0) =>', simplify(correct_answer_parsed - student_answer_parsed) == 0) + print('simplified =>', simplify(correct_answer_parsed - student_answer_parsed)) + print('') + print('Numeric Substitution (c.equals(s)) =>', correct_answer_parsed.equals(student_answer_parsed)) + print('-----------------------------------------------------') diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sectan.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sectan.py new file mode 100755 index 0000000..0e0c7aa --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/sectan.py @@ -0,0 +1,51 @@ +from sympy import * +import sys +sys.path.append("..") + +# # x^2\cdot \left(3\cdot \tan \left([!a!]\cdot x+[!c!]\right)+[!a!]\cdot x\left(\sec \left([!a!]\cdot x+[!c!]\right)\right)^2\right) +# latex1 = "x^2\\cdot \\left(3\\cdot \\tan \\left(2\\cdot x+5\\right)+2\\cdot x\\left(\\sec \\left(2\\cdot x+5\\right)\\right)^2\\right)" +# math1 = process_sympy(latex1) +# print("latex: %s to math: %s" %(latex1,math1)) +# +# latex2 = "x^2\\cdot \\left(3\\cdot \\tan \\left(2\\cdot x+5\\right)+2\\cdot x\\left(\\sec \\left(2\\cdot x+5\\right)^2\\right)\\right)" +# math2 = process_sympy(latex2) +# print("latex: %s to math: %s" %(latex2,math2)) +# +# latex3 = "x^2\\cdot \\left(3\\cdot \\tan \\left(2\\cdot x+5\\right)+2\\cdot x\\left(1+\\tan \\left(2\\cdot x+5\\right)^2\\right)\\right)" +# math3 = process_sympy(latex3) +# print("latex: %s to math: %s" %(latex3,math3)) +# +# print(simplify(math1 - math2)) +# print(simplify(math1 - math3)) + +# +# latex1 = "\\sec^2(2\\cdot x+5)" +# math1 = process_sympy(latex1) +# print("latex: %s to math: %s" %(latex1,math1)) +# +# latex2 = "1+\\tan^2(2\\cdot x+5)" +# math2 = process_sympy(latex2) +# print("latex: %s to math: %s" %(latex2,math2)) +# print(simplify(math1 - math2)) + + +x = Symbol('x', real=True) +y = Symbol('y', real=True) + +# BUG: 1 + tan^2(x+1) should be == sec^2(x+1) but isnt +lhs = (1 + (tan(x + 1))**2) +rhs = (sec(x + 1))**2 +eq = lhs - rhs +print(simplify(lhs)) +print(simplify(rhs)) +print(simplify(eq)) +print(simplify(lhs) == simplify(rhs)) + +# 1 + tan^2(x) == sec^2(x) but isnt +lhs = (1 + (tan(x))**2) +rhs = (sec(x))**2 +eq = lhs - rhs +print(simplify(lhs)) +print(simplify(rhs)) +print(simplify(eq)) +print(simplify(lhs) == simplify(rhs)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/vector.py b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/vector.py new file mode 100755 index 0000000..5b48aee --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/sandbox/vector.py @@ -0,0 +1,75 @@ +import numpy as np +from sympy import * +import sys +sys.path.append("..") + +# row column matrix = vector +v = [1, 2, 3] + +# single column matrix = vector +m = Matrix([1, 2, 3]) +print(m[:, 0]) + +# a three row and 2 column matrix +m = Matrix([[1, 2], [3, 4], [5, 6]]) +print(m[:, 0]) + +# determinant of lin indp system != 0 +m = Matrix([[1, 1], [1, 2]]) +print(m.det()) + +# determinant of lin dep system = 0 +m = Matrix([[1, 1], [2, 2]]) +print(m.det()) + +# determinant of lin dep system = 0 +x = Symbol('x') +y = Symbol('y') +m = Matrix([[x, y], [x, y]]) +print(m.det()) +# Reduced Row-Echelon Form +_, ind = m.rref() +print(len(ind)) + +# determinant of lin dep system != 0 +m = Matrix([[x, y], [y, x]]) +print(m.det()) +# Reduced Row-Echelon Form +_, ind = m.rref() +print(len(ind)) + +# determinant of lin dep system != 0 +# Reduced Row-Echelon Form +m = Matrix([[x, x, y], [y, y, y]]) +_, ind = m.rref() +# Reduced Row-Echelon Form +print(len(ind)) + +#==================# +#===== Numpy ======# +#==================# +# http://kitchingroup.cheme.cmu.edu/blog/2013/03/01/Determining-linear-independence-of-a-set-of-vectors/ +# Lin Indp of set of numerical vectors +TOLERANCE = 1e-14 +v1 = [6, 0, 3, 1, 4, 2] +v2 = [0, -1, 2, 7, 0, 5] +v3 = [12, 3, 0, -19, 8, -11] + +A = np.row_stack([v1, v2, v3]) + +U, s, V = np.linalg.svd(A) +print(s) +print(np.sum(s > TOLERANCE)) + +v1 = [1, 1] +v2 = [4, 4] + +A = np.row_stack([v1, v2]) +U, s, V = np.linalg.svd(A) +print(s) +print(np.sum(s > TOLERANCE)) + + +latex = "\\begin{matrix}1&2\\\\3&4\\end{matrix}" +# math = process_sympy(latex) +print("latex: %s to math: %s" % (latex, 1)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/compile.sh b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/compile.sh new file mode 100755 index 0000000..566d911 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/compile.sh @@ -0,0 +1,9 @@ +#!/bin/sh + +# Get relative path of the root directory of the project +rdir=`git rev-parse --git-dir` +rel_path="$(dirname "$rdir")" +# Change to that path and run the file +cd $rel_path + +java -jar antlr-4.11.1-complete.jar PS.g4 -o gen diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/coverage-ci.sh b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/coverage-ci.sh new file mode 100755 index 0000000..335d4c3 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/coverage-ci.sh @@ -0,0 +1,3 @@ +#!/bin/sh + +pytest --doctest-modules --junitxml=junit/test-results.xml --cov-report=xml --cov-config=.coveragerc --cov=latex2sympy tests
\ No newline at end of file diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/coverage.sh b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/coverage.sh new file mode 100755 index 0000000..a704a21 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/coverage.sh @@ -0,0 +1,23 @@ +#!/bin/sh + +# Get relative path of the root directory of the project +rdir=`git rev-parse --git-dir` +rel_path="$(dirname "$rdir")" +# Change to that path and run the file +cd $rel_path + +# Activate virtual environment +echo "activating venv..." +if test -f .env/bin/activate +then source .env/bin/activate && echo "venv activate (bin)" +elif test -f .env/Scripts/activate +then source .env/Scripts/activate && echo "venv activated (Scripts)" +else exit 1 +fi + +# Run unit test coverage +echo "starting coverage..." +if pytest --doctest-modules --cov-report=html --cov-config=.coveragerc --cov=latex2sympy tests +then echo "coverage finished" +else exit 1 +fi diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/pre-commit b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/pre-commit new file mode 100755 index 0000000..a5ae67c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/pre-commit @@ -0,0 +1,28 @@ +#!/bin/sh + +# Get relative path of the root directory of the project +rdir=`git rev-parse --git-dir` +rel_path="$(dirname "$rdir")" + +# Change to that path and run the file +cd $rel_path + +echo "pre-commit hook started..." + +# Activate virtual environment +echo "activating venv..." +if test -f .env/bin/activate +then source .env/bin/activate && echo "venv activated." +elif test -f .env/Scripts/activate +then source .env/Scripts/activate && echo "venv activated." +else exit 1 +fi + +# Run auto formatting on all staged python files, then add those changes +echo "auto-formatting code..." +if autopep8 --in-place `git diff --name-status --cached | grep '.py' | awk 'match($1, "A|M"){print $2}'` && git add `git diff --name-status --cached | grep '.py' | awk 'match($1, "A|M"){print $2}'` +then echo "code was auto-formatted." +else echo "no code was auto-formatted." +fi + +exit 0 diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/pre-push b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/pre-push new file mode 100755 index 0000000..123ce64 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/pre-push @@ -0,0 +1,28 @@ +#!/bin/sh + +# Get relative path of the root directory of the project +rdir=`git rev-parse --git-dir` +rel_path="$(dirname "$rdir")" + +# Change to that path and run the file +cd $rel_path + +echo "pre-push hook started..." + +# Activate virtual environment +echo "activating venv..." +if test -f .env/bin/activate +then source .env/bin/activate && echo "venv activated." +elif test -f .env/Scripts/activate +then source .env/Scripts/activate && echo "venv activated." +else exit 1 +fi + +# Run unit tests +echo "starting tests..." +# if pytest tests +# then echo "tests finished." +# else exit 1 +# fi + +exit 0 diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/publish.sh b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/publish.sh new file mode 100755 index 0000000..dc12a03 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/publish.sh @@ -0,0 +1,3 @@ +rm ./dist/* +python3 setup.py bdist_wheel +twine upload dist/* diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/setup-hooks.sh b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/setup-hooks.sh new file mode 100755 index 0000000..760dfd5 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/setup-hooks.sh @@ -0,0 +1,3 @@ +#!/bin/sh +cp scripts/pre-push .git/hooks/ +cp scripts/pre-commit .git/hooks/
\ No newline at end of file diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/setup.sh b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/setup.sh new file mode 100755 index 0000000..b7e71c9 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/setup.sh @@ -0,0 +1,42 @@ +#!/bin/sh + +# Get relative path of the root directory of the project +rdir=`git rev-parse --git-dir` +rel_path="$(dirname "$rdir")" +# Change to that path and run the file +cd $rel_path + +echo "creating venv..." +if test -d .env +then echo "venv exists" +else python3 -m venv .env && echo "venv created" +fi + +echo '' +# Activate virtual environment +echo "activating venv..." +if test -f .env/bin/activate +then source .env/bin/activate && echo "venv activate (bin)" +elif test -f .env/Scripts/activate +then source .env/Scripts/activate && echo "venv activated (Scripts)" +else exit 1 +fi + +echo '' +echo "installing requirements..." +if pip install -r dev-requirements.txt +then echo "requirements installed" +else exit 1 +fi + +echo '' +echo "compiling parser..." +sh scripts/compile.sh +echo "parser compiled" + +echo '' +echo "setup git hooks..." +sh scripts/setup-hooks.sh +echo "git hooks setup" + +exit 0 diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/scripts/test.sh b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/test.sh new file mode 100755 index 0000000..20d6b01 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/scripts/test.sh @@ -0,0 +1,31 @@ +#!/bin/sh + +# Get relative path of the root directory of the project +rdir=`git rev-parse --git-dir` +rel_path="$(dirname "$rdir")" +# Change to that path and run the file +cd $rel_path + +# Activate virtual environment +echo "activating venv..." +if test -f .env/bin/activate +then source .env/bin/activate && echo "venv activate (bin)" +elif test -f .env/Scripts/activate +then source .env/Scripts/activate && echo "venv activated (Scripts)" +else exit 1 +fi + +echo '' +echo "compiling parser..." +sh scripts/compile.sh +echo "parser compiled" + +echo '' +# Run unit tests +echo "starting tests..." +if pytest tests +then echo "tests finished" +else exit 1 +fi + +exit 0 diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/setup.cfg b/Qwen2.5-Eval/evaluation/latex2sympy/setup.cfg new file mode 100755 index 0000000..80fb81b --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/setup.cfg @@ -0,0 +1,3 @@ +[pycodestyle] +max-line-length = 120 +ignore = E501 diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/setup.py b/Qwen2.5-Eval/evaluation/latex2sympy/setup.py new file mode 100755 index 0000000..2df9dd2 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/setup.py @@ -0,0 +1,45 @@ +from setuptools import setup, find_packages +from codecs import open +from os import path +here = path.abspath(path.dirname(__file__)) + + +setup( + name="latex2sympy2", + version="1.9.0", + description='Convert latex to sympy with ANTLR and support Matrix, Linear Algebra and CAS functions.', + long_description_content_type='text/markdown', + long_description=open(path.join(here, "README.md"), encoding='utf-8').read(), + # The project's main homepage. + url='https://github.com/ZubinGou/latex2sympy', + # Author details + author='ZubinGou', + author_email='zebgou@gmail.com', + # Choose your license + license='MIT', + classifiers=[ + 'Development Status :: 4 - Beta', + 'Intended Audience :: Developers', + 'Intended Audience :: Education', + 'Intended Audience :: Science/Research', + 'License :: OSI Approved :: MIT License', + 'Topic :: Education', + 'Topic :: Scientific/Engineering :: Mathematics', + 'Topic :: Software Development :: Compilers', + 'Topic :: Text Processing :: Markup :: LaTeX', + 'Topic :: Text Processing :: Markup :: Markdown', + 'Programming Language :: Python :: 3', + 'Programming Language :: Python :: 3.3', + 'Programming Language :: Python :: 3.4', + 'Programming Language :: Python :: 3.5', + 'Programming Language :: Python :: 3.6', + 'Programming Language :: Python :: 3.7', + 'Programming Language :: Python :: 3.8', + ], + packages=find_packages(exclude=('tests')), + py_modules=['asciimath_printer', 'latex2sympy2'], + install_requires=[ + 'sympy>=1.4', + 'antlr4-python3-runtime==4.11.1' + ], +) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/__init__.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/__init__.py new file mode 100755 index 0000000..e69de29 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/__init__.py diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/abs_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/abs_test.py new file mode 100755 index 0000000..37d130c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/abs_test.py @@ -0,0 +1,19 @@ +from .context import assert_equal, get_simple_examples +import pytest +from sympy import Abs + +examples = get_simple_examples(Abs) + +delimiter_pairs = { + '|': '|', + '\\vert': '\\vert', + '\\lvert': '\\rvert' +} + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_abs(input, output, symbolically): + for left, right in delimiter_pairs.items(): + assert_equal("{left}{input}{right}".format(left=left, right=right, input=input), output, symbolically=symbolically) + assert_equal("\\left{left}{input}\\right{right}".format(left=left, right=right, input=input), output, symbolically=symbolically) + assert_equal("\\mleft{left}{input}\\mright{right}".format(left=left, right=right, input=input), output, symbolically=symbolically) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/all_bad_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/all_bad_test.py new file mode 100755 index 0000000..b136313 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/all_bad_test.py @@ -0,0 +1,70 @@ +from .context import assert_equal, process_sympy +import pytest + + +def pytest_generate_tests(metafunc): + metafunc.parametrize('s', metafunc.cls.BAD_STRINGS) + + +class TestAllBad(object): + # These bad latex strings should raise an exception when parsed + BAD_STRINGS = [ + "(", + ")", + # "a / b /", + "\\frac{d}{dx}", + "(\\frac{d}{dx})" + "\\sqrt{}", + "\\sqrt", + "{", + "}", + # "1.1.1", + "\\mathit{TEST}" + "\\frac{2}{}", + "\\frac{}{2}", + "\\int", + # "1 +", + # "a +", + "!", + "!0", + "_", + "^", + # "a // b", + # "a \\cdot \\cdot b", + # "a \\div \\div b", + "a\\mod \\begin{matrix}b\\end{matrix}" + "|", + "||x|", + "\\lfloor x", + "\\lfloor a \\rceil", + "\\operatorname{floor}(12.3, 123.4)", + "()", + "((((((((((((((((()))))))))))))))))", + "-", + "\\frac{d}{dx} + \\frac{d}{dt}", + # "f()", + # "f(,", + # "f(x,,y)", + # "f(x,y,", + "\\sin^x", + "\\cos^2", + # "\\cos 1 \\cos", + # "\\gcd(3)", + # "\\lcm(2)", + "@", "#", "$", "%", "&", "*", + "\\", + "~", + "\\frac{(2 + x}{1 - x)}", + "\\lim_{\\pi \\to 3} a", + # because mix of COMMA and SEMICOLON + "\\left\\{\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix},\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix};\\begin{pmatrix}1\\\\1\\\\1\\end{pmatrix}\\right\\}", + # percentages without numbers before-hand + "a\\%", + "\\%100", + # dollar signs without numbers after + "\\$" + ] + + def test_bad_string(self, s): + with pytest.raises(Exception): + process_sympy(s) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/all_good_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/all_good_test.py new file mode 100755 index 0000000..6d8aa1d --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/all_good_test.py @@ -0,0 +1,284 @@ +from .context import assert_equal, process_sympy, _Add, _Mul, _Pow +import pytest +import hashlib +from sympy import ( + E, I, oo, pi, sqrt, root, Symbol, Add, Mul, Pow, Abs, factorial, log, Eq, Ne, S, Rational, Integer, UnevaluatedExpr, + sin, cos, tan, sinh, cosh, tanh, asin, acos, atan, asinh, acosh, atanh, + csc, sec, Sum, Product, Limit, Integral, Derivative, + LessThan, StrictLessThan, GreaterThan, StrictGreaterThan, + exp, binomial, Matrix, MatMul, MatAdd, + Mod, gcd, lcm, floor, ceiling, Max, Min +) + +x = Symbol('x', real=True) +y = Symbol('y', real=True) +z = Symbol('z', real=True) +a = Symbol('a', real=True) +b = Symbol('b', real=True) +c = Symbol('c', real=True) +f = Symbol('f', real=True) +t = Symbol('t', real=True) +k = Symbol('k', real=True) +n = Symbol('n', real=True) +theta = Symbol('theta', real=True) + +# shorthand definitions + + +def _Abs(a): + return Abs(a, evaluate=False) + + +def _factorial(a): + return factorial(a, evaluate=False) + + +def _log(a, b): + return log(a, b, evaluate=False) + + +def pytest_generate_tests(metafunc): + metafunc.parametrize('s, eq', metafunc.cls.GOOD_PAIRS) + + +class TestAllGood(object): + # These latex strings should parse to the corresponding SymPy expression + GOOD_PAIRS = [ + ("0", 0), + ("1", 1), + ("-3.14", -3.14), + ("5-3", _Add(5, -3)), + ("(-7.13)(1.5)", _Mul(Rational('-7.13'), Rational('1.5'))), + ("\\left(-7.13\\right)\\left(1.5\\right)", _Mul(Rational('-7.13'), Rational('1.5'))), + ("x", x), + ("2x", 2 * x), + ("x^2", x**2), + ("x^{3 + 1}", x**_Add(3, 1)), + ("x^{\\left\\{3 + 1\\right\\}}", x**_Add(3, 1)), + ("-3y + 2x", _Add(_Mul(2, x), Mul(-1, 3, y, evaluate=False))), + ("-c", -c), + ("a \\cdot b", a * b), + ("a / b", a / b), + ("a \\div b", a / b), + ("a + b", a + b), + ("a + b - a", Add(a, b, _Mul(-1, a), evaluate=False)), + ("a^2 + b^2 = c^2", Eq(a**2 + b**2, c**2)), + ("a^2 + b^2 != 2c^2", Ne(a**2 + b**2, 2 * c**2)), + ("a\\mod b", Mod(a, b)), + ("\\sin \\theta", sin(theta)), + ("\\sin(\\theta)", sin(theta)), + ("\\sin\\left(\\theta\\right)", sin(theta)), + ("\\sin^{-1} a", asin(a)), + ("\\sin a \\cos b", _Mul(sin(a), cos(b))), + ("\\sin \\cos \\theta", sin(cos(theta))), + ("\\sin(\\cos \\theta)", sin(cos(theta))), + ("\\arcsin(a)", asin(a)), + ("\\arccos(a)", acos(a)), + ("\\arctan(a)", atan(a)), + ("\\sinh(a)", sinh(a)), + ("\\cosh(a)", cosh(a)), + ("\\tanh(a)", tanh(a)), + ("\\sinh^{-1}(a)", asinh(a)), + ("\\cosh^{-1}(a)", acosh(a)), + ("\\tanh^{-1}(a)", atanh(a)), + ("\\arcsinh(a)", asinh(a)), + ("\\arccosh(a)", acosh(a)), + ("\\arctanh(a)", atanh(a)), + ("\\arsinh(a)", asinh(a)), + ("\\arcosh(a)", acosh(a)), + ("\\artanh(a)", atanh(a)), + ("\\operatorname{arcsinh}(a)", asinh(a)), + ("\\operatorname{arccosh}(a)", acosh(a)), + ("\\operatorname{arctanh}(a)", atanh(a)), + ("\\operatorname{arsinh}(a)", asinh(a)), + ("\\operatorname{arcosh}(a)", acosh(a)), + ("\\operatorname{artanh}(a)", atanh(a)), + ("\\operatorname{gcd}(a, b)", UnevaluatedExpr(gcd(a, b))), + ("\\operatorname{lcm}(a, b)", UnevaluatedExpr(lcm(a, b))), + ("\\operatorname{gcd}(a,b)", UnevaluatedExpr(gcd(a, b))), + ("\\operatorname{lcm}(a,b)", UnevaluatedExpr(lcm(a, b))), + ("\\operatorname{floor}(a)", floor(a)), + ("\\operatorname{ceil}(b)", ceiling(b)), + ("\\cos^2(x)", cos(x)**2), + ("\\cos(x)^2", cos(x)**2), + ("\\gcd(a, b)", UnevaluatedExpr(gcd(a, b))), + ("\\lcm(a, b)", UnevaluatedExpr(lcm(a, b))), + ("\\gcd(a,b)", UnevaluatedExpr(gcd(a, b))), + ("\\lcm(a,b)", UnevaluatedExpr(lcm(a, b))), + ("\\floor(a)", floor(a)), + ("\\ceil(b)", ceiling(b)), + ("\\max(a, b)", Max(a, b)), + ("\\min(a, b)", Min(a, b)), + ("\\frac{a}{b}", a / b), + ("\\frac{a + b}{c}", _Mul(a + b, _Pow(c, -1))), + ("\\frac{7}{3}", _Mul(7, _Pow(3, -1))), + ("(\\csc x)(\\sec y)", csc(x) * sec(y)), + ("\\lim_{x \\to 3} a", Limit(a, x, 3)), + ("\\lim_{x \\rightarrow 3} a", Limit(a, x, 3)), + ("\\lim_{x \\Rightarrow 3} a", Limit(a, x, 3)), + ("\\lim_{x \\longrightarrow 3} a", Limit(a, x, 3)), + ("\\lim_{x \\Longrightarrow 3} a", Limit(a, x, 3)), + ("\\lim_{x \\to 3^{+}} a", Limit(a, x, 3, dir='+')), + ("\\lim_{x \\to 3^{-}} a", Limit(a, x, 3, dir='-')), + ("\\infty", oo), + ("\\infty\\%", oo), + ("\\$\\infty", oo), + ("-\\infty", -oo), + ("-\\infty\\%", -oo), + ("-\\$\\infty", -oo), + ("\\lim_{x \\to \\infty} \\frac{1}{x}", Limit(_Mul(1, _Pow(x, -1)), x, oo)), + ("\\frac{d}{dx} x", Derivative(x, x)), + ("\\frac{d}{dt} x", Derivative(x, t)), + # ("f(x)", f(x)), + # ("f(x, y)", f(x, y)), + # ("f(x, y, z)", f(x, y, z)), + # ("\\frac{d f(x)}{dx}", Derivative(f(x), x)), + # ("\\frac{d\\theta(x)}{dx}", Derivative(theta(x), x)), + ("|x|", _Abs(x)), + ("\\left|x\\right|", _Abs(x)), + ("||x||", _Abs(Abs(x))), + ("|x||y|", _Abs(x) * _Abs(y)), + ("||x||y||", _Abs(_Abs(x) * _Abs(y))), + ("\\lfloor x\\rfloor", floor(x)), + ("\\lceil y\\rceil", ceiling(y)), + ("\\pi^{|xy|}", pi**_Abs(x * y)), + ("\\frac{\\pi}{3}", _Mul(pi, _Pow(3, -1))), + ("\\sin{\\frac{\\pi}{2}}", sin(_Mul(pi, _Pow(2, -1)), evaluate=False)), + ("a+bI", a + I * b), + ("e^{I\\pi}", -1), + ("\\int x dx", Integral(x, x)), + ("\\int x d\\theta", Integral(x, theta)), + ("\\int (x^2 - y)dx", Integral(x**2 - y, x)), + ("\\int x + a dx", Integral(_Add(x, a), x)), + ("\\int da", Integral(1, a)), + ("\\int_0^7 dx", Integral(1, (x, 0, 7))), + ("\\int_a^b x dx", Integral(x, (x, a, b))), + ("\\int^b_a x dx", Integral(x, (x, a, b))), + ("\\int_{a}^b x dx", Integral(x, (x, a, b))), + ("\\int^{b}_a x dx", Integral(x, (x, a, b))), + ("\\int_{a}^{b} x dx", Integral(x, (x, a, b))), + ("\\int_{ }^{}x dx", Integral(x, x)), + ("\\int^{ }_{ }x dx", Integral(x, x)), + ("\\int^{b}_{a} x dx", Integral(x, (x, a, b))), + # ("\\int_{f(a)}^{f(b)} f(z) dz", Integral(f(z), (z, f(a), f(b)))), + ("\\int (x+a)", Integral(_Add(x, a), x)), + ("\\int a + b + c dx", Integral(Add(a, b, c, evaluate=False), x)), + ("\\int \\frac{dz}{z}", Integral(Pow(z, -1), z)), + ("\\int \\frac{3 dz}{z}", Integral(3 * Pow(z, -1), z)), + ("\\int \\frac{1}{x} dx", Integral(Pow(x, -1), x)), + ("\\int \\frac{1}{a} + \\frac{1}{b} dx", Integral(_Add(_Pow(a, -1), Pow(b, -1)), x)), + ("\\int \\frac{3 \\cdot d\\theta}{\\theta}", Integral(3 * _Pow(theta, -1), theta)), + ("\\int \\frac{1}{x} + 1 dx", Integral(_Add(_Pow(x, -1), 1), x)), + ("x_0", Symbol('x_0', real=True)), + ("x_{1}", Symbol('x_1', real=True)), + ("x_a", Symbol('x_a', real=True)), + ("x_{b}", Symbol('x_b', real=True)), + ("h_\\theta", Symbol('h_{\\theta}', real=True)), + ("h_\\theta ", Symbol('h_{\\theta}', real=True)), + ("h_{\\theta}", Symbol('h_{\\theta}', real=True)), + # ("h_{\\theta}(x_0, x_1)", Symbol('h_{theta}', real=True)(Symbol('x_{0}', real=True), Symbol('x_{1}', real=True))), + ("x!", _factorial(x)), + ("100!", _factorial(100)), + ("\\theta!", _factorial(theta)), + ("(x + 1)!", _factorial(_Add(x, 1))), + ("\\left(x + 1\\right)!", _factorial(_Add(x, 1))), + ("(x!)!", _factorial(_factorial(x))), + ("x!!!", _factorial(_factorial(_factorial(x)))), + ("5!7!", _Mul(_factorial(5), _factorial(7))), + ("\\sqrt{x}", sqrt(x)), + ("\\sqrt{x + b}", sqrt(_Add(x, b))), + ("\\sqrt[3]{\\sin x}", root(sin(x), 3)), + ("\\sqrt[y]{\\sin x}", root(sin(x), y)), + ("\\sqrt[\\theta]{\\sin x}", root(sin(x), theta)), + ("x < y", StrictLessThan(x, y)), + ("x \\leq y", LessThan(x, y)), + ("x > y", StrictGreaterThan(x, y)), + ("x \\geq y", GreaterThan(x, y)), + ("\\sum_{k = 1}^{3} c", Sum(c, (k, 1, 3))), + ("\\sum_{k = 1}^3 c", Sum(c, (k, 1, 3))), + ("\\sum^{3}_{k = 1} c", Sum(c, (k, 1, 3))), + ("\\sum^3_{k = 1} c", Sum(c, (k, 1, 3))), + ("\\sum_{k = 1}^{10} k^2", Sum(k**2, (k, 1, 10))), + ("\\sum_{n = 0}^{\\infty} \\frac{1}{n!}", Sum(_Pow(_factorial(n), -1), (n, 0, oo))), + ("\\prod_{a = b}^{c} x", Product(x, (a, b, c))), + ("\\prod_{a = b}^c x", Product(x, (a, b, c))), + ("\\prod^{c}_{a = b} x", Product(x, (a, b, c))), + ("\\prod^c_{a = b} x", Product(x, (a, b, c))), + ("\\ln x", _log(x, E)), + ("\\ln xy", _log(x * y, E)), + ("\\log x", _log(x, 10)), + ("\\log xy", _log(x * y, 10)), + # ("\\log_2 x", _log(x, 2)), + ("\\log_{2} x", _log(x, 2)), + # ("\\log_a x", _log(x, a)), + ("\\log_{a} x", _log(x, a)), + ("\\log_{11} x", _log(x, 11)), + ("\\log_{a^2} x", _log(x, _Pow(a, 2))), + ("[x]", x), + ("[a + b]", _Add(a, b)), + ("\\frac{d}{dx} [ \\tan x ]", Derivative(tan(x), x)), + ("2\\overline{x}", 2 * Symbol('xbar', real=True)), + ("2\\overline{x}_n", 2 * Symbol('xbar_n', real=True)), + ("\\frac{x}{\\overline{x}_n}", x / Symbol('xbar_n', real=True)), + ("\\frac{\\sin(x)}{\\overline{x}_n}", sin(Symbol('x', real=True)) / Symbol('xbar_n', real=True)), + ("2\\bar{x}", 2 * Symbol('xbar', real=True)), + ("2\\bar{x}_n", 2 * Symbol('xbar_n', real=True)), + ("\\sin\\left(\\theta\\right) \\cdot4", sin(theta) * 4), + ("\\ln\\left(\\theta\\right)", _log(theta, E)), + ("\\ln\\left(x-\\theta\\right)", _log(x - theta, E)), + ("\\ln\\left(\\left(x-\\theta\\right)\\right)", _log(x - theta, E)), + ("\\ln\\left(\\left[x-\\theta\\right]\\right)", _log(x - theta, E)), + ("\\ln\\left(\\left\\{x-\\theta\\right\\}\\right)", _log(x - theta, E)), + ("\\ln\\left(\\left|x-\\theta\\right|\\right)", _log(_Abs(x - theta), E)), + ("\\frac{1}{2}xy(x+y)", Mul(_Pow(2, -1), x, y, (x + y), evaluate=False)), + ("\\frac{1}{2}\\theta(x+y)", Mul(_Pow(2, -1), theta, (x + y), evaluate=False)), + ("1-f(x)", 1 - f * x), + + ("\\begin{matrix}1&2\\\\3&4\\end{matrix}", Matrix([[1, 2], [3, 4]])), + ("\\begin{matrix}x&x^2\\\\\\sqrt{x}&x\\end{matrix}", Matrix([[x, x**2], [_Pow(x, S.Half), x]])), + ("\\begin{matrix}\\sqrt{x}\\\\\\sin(\\theta)\\end{matrix}", Matrix([_Pow(x, S.Half), sin(theta)])), + ("\\begin{pmatrix}1&2\\\\3&4\\end{pmatrix}", Matrix([[1, 2], [3, 4]])), + ("\\begin{bmatrix}1&2\\\\3&4\\end{bmatrix}", Matrix([[1, 2], [3, 4]])), + + # scientific notation + ("2.5\\times 10^2", 250), + ("1,500\\times 10^{-1}", 150), + + # e notation + ("2.5E2", 250), + ("1,500E-1", 150), + + # multiplication without cmd + ("2x2y", Mul(2, x, 2, y, evaluate=False)), + ("2x2", Mul(2, x, 2, evaluate=False)), + ("x2", x * 2), + + # lin alg processing + ("\\theta\\begin{matrix}1&2\\\\3&4\\end{matrix}", MatMul(theta, Matrix([[1, 2], [3, 4]]), evaluate=False)), + ("\\theta\\begin{matrix}1\\\\3\\end{matrix} - \\begin{matrix}-1\\\\2\\end{matrix}", MatAdd(MatMul(theta, Matrix([[1], [3]]), evaluate=False), MatMul(-1, Matrix([[-1], [2]]), evaluate=False), evaluate=False)), + ("\\theta\\begin{matrix}1&0\\\\0&1\\end{matrix}*\\begin{matrix}3\\\\-2\\end{matrix}", MatMul(theta, Matrix([[1, 0], [0, 1]]), Matrix([3, -2]), evaluate=False)), + ("\\frac{1}{9}\\theta\\begin{matrix}1&2\\\\3&4\\end{matrix}", MatMul(Pow(9, -1, evaluate=False), theta, Matrix([[1, 2], [3, 4]]), evaluate=False)), + ("\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix},\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix}", [Matrix([1, 2, 3]), Matrix([4, 3, 1])]), + ("\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix};\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix}", [Matrix([1, 2, 3]), Matrix([4, 3, 1])]), + ("\\left\\{\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix},\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix}\\right\\}", [Matrix([1, 2, 3]), Matrix([4, 3, 1])]), + ("\\left\\{\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix},\\begin{pmatrix}4\\\\3\\\\1\\end{pmatrix},\\begin{pmatrix}1\\\\1\\\\1\\end{pmatrix}\\right\\}", [Matrix([1, 2, 3]), Matrix([4, 3, 1]), Matrix([1, 1, 1])]), + ("\\left\\{\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix}\\right\\}", Matrix([1, 2, 3])), + ("\\left{\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix}\\right}", Matrix([1, 2, 3])), + ("{\\begin{pmatrix}1\\\\2\\\\3\\end{pmatrix}}", Matrix([1, 2, 3])), + + # us dollars + ("\\$1,000.00", 1000), + ("\\$543.21", 543.21), + ("\\$0.009", 0.009), + + # percentages + ("100\\%", 1), + ("1.5\\%", 0.015), + ("0.05\\%", 0.0005), + + # empty set + ("\\emptyset", S.EmptySet) + ] + + def test_good_pair(self, s, eq): + assert_equal(s, eq) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/atom_expr_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/atom_expr_test.py new file mode 100755 index 0000000..23b69b4 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/atom_expr_test.py @@ -0,0 +1,58 @@ +from .context import assert_equal +import pytest +from sympy import Symbol, Integer, Pow + +# label, text, symbol_text +symbols = [ + ('letter', 'x', 'x'), + ('greek letter', '\\lambda', 'lambda'), + ('greek letter w/ space', '\\alpha ', 'alpha'), + ('accented letter', '\\overline{x}', 'xbar') +] + +subscripts = [ + ('2'), + ('{23}'), + ('i'), + ('{ij}'), + ('{i,j}'), + ('{good}'), + ('{x^2}') +] + +examples = [] +for symbol in symbols: + for subscript in subscripts: + examples.append(tuple(list(symbol) + [subscript])) + + +@pytest.mark.parametrize('label, text, symbol_text, subscript', examples) +def test_with_supexpr(label, text, symbol_text, subscript): + assert_equal(text + '^2', Pow(Symbol(symbol_text, real=True), Integer(2))) + + +@pytest.mark.parametrize('label, text, symbol_text, subscript', examples) +def test_with_subexpr(label, text, symbol_text, subscript): + assert_equal(text + '_' + subscript, Symbol(symbol_text + '_' + subscript, real=True)) + + +@pytest.mark.parametrize('label, text, symbol_text, subscript', examples) +def test_with_subexpr_before_supexpr(label, text, symbol_text, subscript): + assert_equal(text + '_' + subscript + '^2', Pow(Symbol(symbol_text + '_' + subscript, real=True), Integer(2))) + + +@pytest.mark.parametrize('label, text, symbol_text, subscript', examples) +def test_with_subexpr_before_supexpr_with_braces(label, text, symbol_text, subscript): + wrapped_subscript = subscript if '{' in subscript else '{' + subscript + '}' + assert_equal(text + '_' + wrapped_subscript + '^{2}', Pow(Symbol(symbol_text + '_' + subscript, real=True), Integer(2))) + + +@pytest.mark.parametrize('label, text, symbol_text, subscript', examples) +def test_with_supexpr_before_subexpr(label, text, symbol_text, subscript): + assert_equal(text + '^2_' + subscript, Pow(Symbol(symbol_text + '_' + subscript, real=True), Integer(2))) + + +@pytest.mark.parametrize('label, text, symbol_text, subscript', examples) +def test_with_supexpr_before_subexpr_with_braces(label, text, symbol_text, subscript): + wrapped_subscript = subscript if '{' in subscript else '{' + subscript + '}' + assert_equal(text + '^{2}_' + wrapped_subscript, Pow(Symbol(symbol_text + '_' + subscript, real=True), Integer(2))) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/binomial_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/binomial_test.py new file mode 100755 index 0000000..2fec010 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/binomial_test.py @@ -0,0 +1,36 @@ +from .context import assert_equal, _Add, _Mul, _Pow +import pytest +from sympy import binomial, Symbol + +x = Symbol('x', real=True) +y = Symbol('y', real=True) +theta = Symbol('theta', real=True) +gamma = Symbol('gamma', real=True) + + +def test_binomial_numeric(): + assert_equal("\\binom{16}{2}", binomial(16, 2)) + + +def test_binomial_symbols(): + assert_equal("\\binom{x}{y}", binomial(x, y)) + + +def test_binomial_greek_symbols(): + assert_equal("\\binom{\\theta}{\\gamma}", binomial(theta, gamma)) + + +def test_binomial_expr(): + assert_equal("\\binom{16+2}{\\frac{4}{2}}", binomial(_Add(16, 2), _Mul(4, _Pow(2, -1)), evaluate=False)) + + +def test_choose_numeric(): + assert_equal("\\choose{16}{2}", binomial(16, 2)) + + +def test_choose_symbols(): + assert_equal("\\choose{x}{y}", binomial(x, y)) + + +def test_choose_greek_symbols(): + assert_equal("\\choose{\\theta}{\\gamma}", binomial(theta, gamma)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/ceil_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/ceil_test.py new file mode 100755 index 0000000..f4c419c --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/ceil_test.py @@ -0,0 +1,29 @@ +from .context import assert_equal, get_simple_examples +import pytest +from sympy import ceiling + +examples = get_simple_examples(ceiling) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_ceil_func(input, output, symbolically): + assert_equal("\\ceil({input})".format(input=input), output, symbolically=symbolically) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_ceil_operatorname(input, output, symbolically): + assert_equal("\\operatorname{{ceil}}({input})".format(input=input), output, symbolically=symbolically) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_ceil_cmd(input, output, symbolically): + assert_equal("\\lceil {input}\\rceil".format(input=input), output, symbolically=symbolically) + assert_equal("\\left\\lceil {input}\\right\\rceil".format(input=input), output, symbolically=symbolically) + assert_equal("\\mleft\\lceil {input}\\mright\\rceil".format(input=input), output, symbolically=symbolically) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_ceil_corners(input, output, symbolically): + assert_equal("\\ulcorner {input}\\urcorner".format(input=input), output, symbolically=symbolically) + assert_equal("\\left\\ulcorner {input}\\right\\urcorner".format(input=input), output, symbolically=symbolically) + assert_equal("\\mleft\\ulcorner {input}\\mright\\urcorner".format(input=input), output, symbolically=symbolically) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/complex_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/complex_test.py new file mode 100755 index 0000000..2197141 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/complex_test.py @@ -0,0 +1,21 @@ +from .context import assert_equal +import pytest +from sympy import Sum, I, Symbol, Integer + +a = Symbol('a', real=True) +b = Symbol('b', real=True) +i = Symbol('i', real=True) +n = Symbol('n', real=True) +x = Symbol('x', real=True) + + +def test_complex(): + assert_equal("a+Ib", a + I * b) + + +def test_complex_e(): + assert_equal("e^{I\\pi}", Integer(-1)) + + +def test_complex_sum(): + assert_equal("\\sum_{i=0}^{n} i \\cdot x", Sum(i * x, (i, 0, n))) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/context.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/context.py new file mode 100755 index 0000000..f48cfd3 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/context.py @@ -0,0 +1,84 @@ +from sympy import simplify, srepr, Add, Mul, Pow, Rational, pi, sqrt, Symbol +from latex2sympy.latex2sympy2 import latex2sympy as process_sympy +import sys +import os +sys.path.insert(0, os.path.abspath(os.path.join(os.path.dirname(__file__), '..'))) + +x = Symbol('x', real=True) +y = Symbol('y', real=True) + +# shorthand definitions + + +def _Add(a, b): + return Add(a, b, evaluate=False) + + +def _Mul(a, b): + return Mul(a, b, evaluate=False) + + +def _Pow(a, b): + return Pow(a, b, evaluate=False) + + +def get_simple_examples(func): + ''' + Returns an array of tuples, containing the string `input`, sympy `output` using the provided sympy `func`, and `symbolically` boolean + for calling `compare`. + ''' + return [ + ("1.1", func(1.1), False), + ("6.9", func(6.9), False), + ("3.5", func(3.5), False), + ("8", func(8), False), + ("0", func(0), False), + ("290348E32", func(Rational('290348E32')), False), + ("1237.293894239480234", func(Rational('1237.293894239480234')), False), + ("8623.4592104E-2", func(Rational('8623.4592104E-2')), False), + ("\\pi ", func(pi), False), + ("\\sqrt{100}", func(sqrt(100)), False), + ("12,123.4", func(Rational('12123.4')), False), + ("-9.4", func(-9.4), False), + ("-35.9825", func(-35.9825), False), + ("-\\sqrt{5}", func(-sqrt(5)), False), + ("-324E-3", func(Rational('-324E-3')), False), + ("-0.23", func(-0.23), False), + ("\\frac{1}{2}", func(Rational('1/2')), False), + ("\\frac{6}{2}", func(Rational('6/2')), False), + ("\\frac{9}{5}", func(Rational('9/5')), False), + ("\\frac{-42}{6}", func(Rational('-42/6')), False), + ("-\\frac{325}{3}", func(Rational('-325/3')), False), + ("\\frac{\\pi }{2}", func(pi / 2), False), + ("(1+6)/3", func(Rational(1 + 6, 3)), False), + ("1+6/3", func(1 + Rational('6/3')), False), + ("7*4/5", func(7 * 4 / 5), False), + ("15-2.3", func(15 - Rational('2.3')), False), + ("x", func(x), True), + ("x + y", func(x + y), True), + ("\\frac{9x}{4}", func(9 * x / 4), True), + ("y\\pi", func(y * pi), True), + ("2y-y-y", func(2 * y - y - y), True) + ] + + +def compare(actual, expected, symbolically=False): + if symbolically: + assert simplify(actual - expected) == 0 + else: + actual_exp_tree = srepr(actual) + expected_exp_tree = srepr(expected) + try: + assert actual_exp_tree == expected_exp_tree + except Exception: + if isinstance(actual, int) or isinstance(actual, float) or actual.is_number and isinstance(expected, int) or isinstance(expected, float) or expected.is_number: + assert actual == expected or actual - expected == 0 or simplify(actual - expected) == 0 + else: + print('expected_exp_tree = ', expected_exp_tree) + print('actual exp tree = ', actual_exp_tree) + raise + + +def assert_equal(latex, expr, variable_values={}, symbolically=False): + parsed = process_sympy(latex, variable_values) + compare(parsed, expr, symbolically) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/exp_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/exp_test.py new file mode 100755 index 0000000..1ef20c6 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/exp_test.py @@ -0,0 +1,57 @@ +from .context import assert_equal +import pytest +from sympy import exp, sin, Symbol, E + +x = Symbol('x', real=True) +y = Symbol('y', real=True) + + +def test_exp_letter(): + assert_equal("e", E) + assert_equal("e", exp(1)) + + +def test_exp_func(): + assert_equal("\\exp(3)", exp(3)) + + +def test_exp_func_no_delim(): + assert_equal("\\exp3", exp(3)) + + +def test_exp_command_symbol(): + assert_equal("\\exponentialE", E) + assert_equal("\\exponentialE", exp(1)) + + +def test_exp_command_symbol_expression(): + assert_equal("\\exponentialE^{3}", exp(3)) + + +def test_exp_command_symbol_multiplied(): + ''' + \\exponentialE is NOT a function, so using the following notation equates to multiplication + ''' + assert_equal("\\exponentialE (3)", E * 3) + assert_equal("\\exponentialE \\left( 3\\right)", E * 3) + assert_equal("\\exponentialE \\times 3", E * 3) + + +def test_exp_numeric(): + assert_equal("e^3", exp(3)) + + +def test_exp_symbol(): + assert_equal("e^x", exp(x)) + + +def test_exp_symbol_expr(): + assert_equal("e^{x+y}", exp(x + y)) + + +def test_exp_symbol_expr_group(): + assert_equal("e^{(x+y)}", exp(x + y)) + + +def test_exp_expr(): + assert_equal("\\sin(x)*e^x", sin(x) * exp(x)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/floor_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/floor_test.py new file mode 100755 index 0000000..3961782 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/floor_test.py @@ -0,0 +1,29 @@ +from .context import assert_equal, get_simple_examples +import pytest +from sympy import floor + +examples = get_simple_examples(floor) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_floor_func(input, output, symbolically): + assert_equal("\\floor({input})".format(input=input), output, symbolically=symbolically) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_floor_operatorname(input, output, symbolically): + assert_equal("\\operatorname{{floor}}({input})".format(input=input), output, symbolically=symbolically) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_floor_cmd(input, output, symbolically): + assert_equal("\\lfloor {input}\\rfloor".format(input=input), output, symbolically=symbolically) + assert_equal("\\left\\lfloor {input}\\right\\rfloor".format(input=input), output, symbolically=symbolically) + assert_equal("\\mleft\\lfloor {input}\\mright\\rfloor".format(input=input), output, symbolically=symbolically) + + +@pytest.mark.parametrize('input, output, symbolically', examples) +def test_floor_corners(input, output, symbolically): + assert_equal("\\llcorner {input}\\lrcorner".format(input=input), output, symbolically=symbolically) + assert_equal("\\left\\llcorner {input}\\right\\lrcorner".format(input=input), output, symbolically=symbolically) + assert_equal("\\mleft\\llcorner {input}\\mright\\lrcorner".format(input=input), output, symbolically=symbolically) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/gcd_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/gcd_test.py new file mode 100755 index 0000000..a45a215 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/gcd_test.py @@ -0,0 +1,161 @@ +from .context import assert_equal +import pytest +from sympy import Symbol, Rational, UnevaluatedExpr, gcd, igcd, sqrt, pi + +x = Symbol('x', real=True) +y = Symbol('y', real=True) +z = Symbol('z', real=True) + + +def test_gcd_usual(): + assert_equal("\\gcd(18, 3)", gcd(18, 3)) + assert_equal("\\gcd(3, 18)", gcd(3, 18)) + assert_equal("\\gcd(2, 2)", gcd(2, 2)) + assert_equal("\\gcd(0, 21)", UnevaluatedExpr(gcd(0, 21))) + assert_equal("\\gcd(21, 0)", UnevaluatedExpr(gcd(21, 0))) + assert_equal("\\gcd(0, 0)", UnevaluatedExpr(gcd(0, 0))) + assert_equal("\\gcd(6128, 24)", gcd(6128, 24)) + assert_equal("\\gcd(24, 6128)", gcd(24, 6128)) + assert_equal("\\gcd(1E20, 1000000)", gcd(Rational('1E20'), 1000000)) + assert_equal("\\gcd(128*10^32, 1)", gcd(Rational('128E32'), 1)) + + assert_equal("\\operatorname{gcd}(18, 3)", gcd(18, 3)) + assert_equal("\\operatorname{gcd}(3, 18)", gcd(3, 18)) + assert_equal("\\operatorname{gcd}(2, 2)", gcd(2, 2)) + assert_equal("\\operatorname{gcd}(0, 21)", UnevaluatedExpr(gcd(0, 21))) + assert_equal("\\operatorname{gcd}(21, 0)", UnevaluatedExpr(gcd(21, 0))) + assert_equal("\\operatorname{gcd}(0, 0)", UnevaluatedExpr(gcd(0, 0))) + assert_equal("\\operatorname{gcd}(6128, 24)", gcd(6128, 24)) + assert_equal("\\operatorname{gcd}(24, 6128)", gcd(24, 6128)) + assert_equal("\\operatorname{gcd}(1E20, 1000000)", gcd(Rational('1E20'), 1000000)) + assert_equal("\\operatorname{gcd}(128*10^32, 1)", gcd(Rational('128E32'), 1)) + + +def test_gcd_negative(): + assert_equal("\\gcd(-12, 4)", gcd(-12, 4)) + assert_equal("\\gcd(219, -9)", gcd(219, -9)) + assert_equal("\\gcd(-8, -64)", gcd(-8, -64)) + assert_equal("\\gcd(-5, -5)", gcd(-5, -5)) + assert_equal("\\gcd(-1, 182033)", gcd(-1, 182033)) + assert_equal("\\gcd(25, -6125)", gcd(25, -6125)) + assert_equal("\\gcd(243, -2.9543127E21)", gcd(243, Rational('-2.9543127E21'))) + + assert_equal("\\operatorname{gcd}(-12, 4)", gcd(-12, 4)) + assert_equal("\\operatorname{gcd}(219, -9)", gcd(219, -9)) + assert_equal("\\operatorname{gcd}(-8, -64)", gcd(-8, -64)) + assert_equal("\\operatorname{gcd}(-5, -5)", gcd(-5, -5)) + assert_equal("\\operatorname{gcd}(-1, 182033)", gcd(-1, 182033)) + assert_equal("\\operatorname{gcd}(25, -6125)", gcd(25, -6125)) + assert_equal("\\operatorname{gcd}(243, -2.9543127E21)", gcd(243, Rational('-2.9543127E21'))) + + +def test_gcd_float(): + assert_equal("\\gcd(2.4, 3.6)", gcd(Rational('2.4'), Rational('3.6'))) + assert_equal("\\gcd(3.6, 2.4)", gcd(Rational('3.6'), Rational('2.4'))) + assert_equal("\\gcd(\\pi, 3)", gcd(pi, 3)) + assert_equal("\\gcd(618, 1.5)", gcd(618, Rational('1.5'))) + assert_equal("\\gcd(-1.5, 618)", gcd(Rational('-1.5'), 618)) + assert_equal("\\gcd(0.42, 2)", gcd(Rational('0.42'), 2)) + assert_equal("\\gcd(1.43E-13, 21)", gcd(Rational('1.43E-13'), 21)) + assert_equal("\\gcd(21, -143E-13)", gcd(21, Rational('-143E-13'))) + assert_equal("\\gcd(9.80655, 9.80655)", gcd(Rational('9.80655'), Rational('9.80655'))) + assert_equal("\\gcd(0.0000923423, -8341.234802909)", gcd(Rational('0.0000923423'), Rational('-8341.234802909'))) + assert_equal("\\gcd(\\sqrt{5}, \\sqrt{2})", gcd(sqrt(5), sqrt(2))) + + assert_equal("\\operatorname{gcd}(2.4, 3.6)", gcd(Rational('2.4'), Rational('3.6'))) + assert_equal("\\operatorname{gcd}(3.6, 2.4)", gcd(Rational('3.6'), Rational('2.4'))) + assert_equal("\\operatorname{gcd}(\\pi, 3)", gcd(pi, 3)) + assert_equal("\\operatorname{gcd}(618, 1.5)", gcd(618, Rational('1.5'))) + assert_equal("\\operatorname{gcd}(-1.5, 618)", gcd(Rational('-1.5'), 618)) + assert_equal("\\operatorname{gcd}(0.42, 2)", gcd(Rational('0.42'), 2)) + assert_equal("\\operatorname{gcd}(1.43E-13, 21)", gcd(Rational('1.43E-13'), 21)) + assert_equal("\\operatorname{gcd}(21, -143E-13)", gcd(21, Rational('-143E-13'))) + assert_equal("\\operatorname{gcd}(9.80655, 9.80655)", gcd(Rational('9.80655'), Rational('9.80655'))) + assert_equal("\\operatorname{gcd}(0.0000923423, -8341.234802909)", gcd(Rational('0.0000923423'), Rational('-8341.234802909'))) + assert_equal("\\operatorname{gcd}(\\sqrt{5}, \\sqrt{2})", gcd(sqrt(5), sqrt(2))) + + +def test_gcd_fraction(): + assert_equal("\\gcd(1/2, 3)", gcd(Rational('1/2'), 3)) + assert_equal("\\gcd(3, 1/2)", gcd(3, Rational('1/2'))) + assert_equal("\\gcd(6/2, 3)", gcd(Rational('6/2'), 3)) + assert_equal("\\gcd(1/10, 1/10)", gcd(Rational('1/10'), Rational('1/10'))) + assert_equal("\\gcd(42, 42/6)", gcd(42, Rational('42/6'))) + assert_equal("\\gcd(10000000/10, 10000)", gcd(Rational('10000000/10'), 10000)) + + assert_equal("\\operatorname{gcd}(1/2, 3)", gcd(Rational('1/2'), 3)) + assert_equal("\\operatorname{gcd}(3, 1/2)", gcd(3, Rational('1/2'))) + assert_equal("\\operatorname{gcd}(6/2, 3)", gcd(Rational('6/2'), 3)) + assert_equal("\\operatorname{gcd}(1/10, 1/10)", gcd(Rational('1/10'), Rational('1/10'))) + assert_equal("\\operatorname{gcd}(42, 42/6)", gcd(42, Rational('42/6'))) + assert_equal("\\operatorname{gcd}(10000000/10, 10000)", gcd(Rational('10000000/10'), 10000)) + + +def test_gcd_expr(): + assert_equal("\\gcd(1+1, 8)", gcd(1 + 1, 8)) + assert_equal("920*\\gcd(9, 12*4/2)", 920 * gcd(9, 12 * Rational('4/2'))) + assert_equal("\\gcd(32-128, 10)*22", gcd(32 - 128, 10) * 22) + assert_equal("\\sqrt{\\gcd(1.25E24, 1E12)}", sqrt(gcd(Rational('1.25E24'), Rational('1E12')))) + assert_equal("\\gcd(92.0, 000+2)", gcd(Rational('92.0'), 000 + 2)) + + assert_equal("\\operatorname{gcd}(1+1, 8)", gcd(1 + 1, 8)) + assert_equal("920*\\operatorname{gcd}(9, 12*4/2)", 920 * gcd(9, 12 * Rational('4/2'))) + assert_equal("\\operatorname{gcd}(32-128, 10)*22", gcd(32 - 128, 10) * 22) + assert_equal("\\sqrt{\\operatorname{gcd}(1.25E24, 1E12)}", sqrt(gcd(Rational('1.25E24'), Rational('1E12')))) + assert_equal("\\operatorname{gcd}(92.0, 000+2)", gcd(Rational('92.0'), 000 + 2)) + + +def test_gcd_symbol(): + assert_equal("\\gcd(x, y)", gcd(x, y), symbolically=True) + assert_equal("\\gcd(y, -x)", gcd(y, -x), symbolically=True) + assert_equal("\\gcd(2y, x)", gcd(2 * y, x), symbolically=True) + assert_equal("\\gcd(125, 50x)", gcd(125, 50 * x), symbolically=True) + assert_equal("\\gcd(x + 76, \\sqrt{x} * 4)", gcd(x + 76, sqrt(x) * 4), symbolically=True) + assert_equal("\\gcd(y, y)", gcd(y, y), symbolically=True) + assert_equal("y + \\gcd(0.4x, 8/3) / 2", y + gcd(Rational('0.4') * x, Rational('8/3')) / 2, symbolically=True) + assert_equal("6.673E-11 * (\\gcd(8.85418782E-12, 9x) + 4) / 8y", Rational('6.673E-11') * (gcd(Rational('8.85418782E-12'), 9 * x) + 4) / (8 * y), symbolically=True) + + assert_equal("\\operatorname{gcd}(x, y)", gcd(x, y), symbolically=True) + assert_equal("\\operatorname{gcd}(y, -x)", gcd(y, -x), symbolically=True) + assert_equal("\\operatorname{gcd}(2y, x)", gcd(2 * y, x), symbolically=True) + assert_equal("\\operatorname{gcd}(125, 50x)", gcd(125, 50 * x), symbolically=True) + assert_equal("\\operatorname{gcd}(x + 76, \\sqrt{x} * 4)", gcd(x + 76, sqrt(x) * 4), symbolically=True) + assert_equal("\\operatorname{gcd}(y, y)", gcd(y, y), symbolically=True) + assert_equal("y + \\operatorname{gcd}(0.4x, 8/3) / 2", y + gcd(Rational('0.4') * x, Rational('8/3')) / 2, symbolically=True) + assert_equal("6.673E-11 * (\\operatorname{gcd}(8.85418782E-12, 9x) + 4) / 8y", Rational('6.673E-11') * (gcd(Rational('8.85418782E-12'), 9 * x) + 4) / (8 * y), symbolically=True) + + +def test_multiple_parameters(): + assert_equal("\\gcd(830,450)", gcd(830, 450)) + assert_equal("\\gcd(6,321,429)", igcd(6, 321, 429)) + assert_equal("\\gcd(14,2324)", gcd(14, 2324)) + assert_equal("\\gcd(3, 6, 2)", igcd(3, 6, 2)) + assert_equal("\\gcd(144, 2988, 37116)", igcd(144, 2988, 37116)) + assert_equal("\\gcd(144,2988, 37116,18, 72)", igcd(144, 2988, 37116, 18, 72)) + assert_equal("\\gcd(144, 2988, 37116, 18, 72, 12, 6)", igcd(144, 2988, 37116, 18, 72, 12, 6)) + assert_equal("\\gcd(32)", gcd(32, 32)) + assert_equal("\\gcd(-8, 4,-2)", gcd(-8, gcd(4, -2))) + assert_equal("\\gcd(x, y,z)", gcd(x, gcd(y, z)), symbolically=True) + assert_equal("\\gcd(6*4,48, 3)", igcd(6 * 4, 48, 3)) + assert_equal("\\gcd(6*4,48,3)", igcd(6 * 4, 48, 3)) + assert_equal("\\gcd(2.4,3.6, 0.6)", gcd(Rational('2.4'), gcd(Rational('3.6'), Rational('0.6')))) + assert_equal("\\gcd(2.4,3.6,0.6)", gcd(Rational('2.4'), gcd(Rational('3.6'), Rational('0.6')))) + assert_equal("\\gcd(\\sqrt{3},\\sqrt{2}, \\sqrt{100})", gcd(sqrt(3), gcd(sqrt(2), sqrt(100)))) + assert_equal("\\gcd(1E12, 1E6,1E3, 10)", igcd(Rational('1E12'), Rational('1E6'), Rational('1E3'), 10)) + + assert_equal("\\operatorname{gcd}(830,450)", gcd(830, 450)) + assert_equal("\\operatorname{gcd}(6,321,429)", igcd(6, 321, 429)) + assert_equal("\\operatorname{gcd}(14,2324)", gcd(14, 2324)) + assert_equal("\\operatorname{gcd}(3, 6, 2)", igcd(3, 6, 2)) + assert_equal("\\operatorname{gcd}(144, 2988, 37116)", igcd(144, 2988, 37116)) + assert_equal("\\operatorname{gcd}(144,2988, 37116,18, 72)", igcd(144, 2988, 37116, 18, 72)) + assert_equal("\\operatorname{gcd}(144, 2988, 37116, 18, 72, 12, 6)", igcd(144, 2988, 37116, 18, 72, 12, 6)) + assert_equal("\\operatorname{gcd}(32)", gcd(32, 32)) + assert_equal("\\operatorname{gcd}(-8, 4,-2)", gcd(-8, gcd(4, -2))) + assert_equal("\\operatorname{gcd}(x, y,z)", gcd(x, gcd(y, z)), symbolically=True) + assert_equal("\\operatorname{gcd}(6*4,48, 3)", igcd(6 * 4, 48, 3)) + assert_equal("\\operatorname{gcd}(6*4,48,3)", igcd(6 * 4, 48, 3)) + assert_equal("\\operatorname{gcd}(2.4,3.6, 0.6)", gcd(Rational('2.4'), gcd(Rational('3.6'), Rational('0.6')))) + assert_equal("\\operatorname{gcd}(2.4,3.6,0.6)", gcd(Rational('2.4'), gcd(Rational('3.6'), Rational('0.6')))) + assert_equal("\\operatorname{gcd}(\\sqrt{3},\\sqrt{2}, \\sqrt{100})", gcd(sqrt(3), gcd(sqrt(2), sqrt(100)))) + assert_equal("\\operatorname{gcd}(1E12, 1E6,1E3, 10)", igcd(Rational('1E12'), Rational('1E6'), Rational('1E3'), 10)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/greek_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/greek_test.py new file mode 100755 index 0000000..1e23a0d --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/greek_test.py @@ -0,0 +1,19 @@ +from .context import assert_equal +import pytest +from sympy import Symbol + +epsilon_upper = Symbol('char"000190', real=True) +epsilon_lower = Symbol('epsilon', real=True) +varepsilon = Symbol('varepsilon', real=True) + + +def test_greek_epsilon(): + assert_equal("\\epsilon", epsilon_lower) + + +def test_greek_epsilon_upper(): + assert_equal('\\char"000190', epsilon_upper) + + +def test_greek_varepsilon(): + assert_equal('\\varepsilon', varepsilon) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/grouping_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/grouping_test.py new file mode 100755 index 0000000..139f3f1 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/grouping_test.py @@ -0,0 +1,52 @@ +from .context import assert_equal, _Pow, _Add, _Mul +import pytest +from sympy import Integral, sin, Symbol, Mul, Integer, Pow +from latex2sympy.latex2sympy2 import latex2sympy as process_sympy + +a = Symbol('a', real=True) +b = Symbol('b', real=True) +x = Symbol('x', real=True) +theta = Symbol('theta', real=True) + + +func_arg_examples = [ + ('\\int ', 'x dx', Integral(x, x)), + ('\\sin', '\\theta ', sin(theta)) +] + +example_groups = [ + ('1+2', '3-4', _Mul(_Add(1, 2), _Add(3, _Mul(-1, 4)))) +] + +modifiable_delimiter_pairs = { + '(': ')', + '\\lgroup': '\\rgroup', + '\\{': '\\}', + '\\lbrace': '\\rbrace', + '[': ']', + '\\lbrack': '\\rbrack', +} + + +@pytest.mark.parametrize('func, args, output', func_arg_examples) +def test_func_arg_groupings(func, args, output): + # none + assert_equal("{func} {args}".format(func=func, args=args), output) + # normal brace (not modifiable) + assert_equal("{func}{{{args}}}".format(func=func, args=args), output) + # rest of delimiters, with modifications + for left, right in modifiable_delimiter_pairs.items(): + assert_equal("{func}{left}{args}{right}".format(left=left, right=right, func=func, args=args), output) + assert_equal("{func}\\left{left}{args}\\right{right}".format(left=left, right=right, func=func, args=args), output) + assert_equal("{func}\\mleft{left}{args}\\mright{right}".format(left=left, right=right, func=func, args=args), output) + + +@pytest.mark.parametrize('group1, group2, output', example_groups) +def test_delimiter_groupings(group1, group2, output): + # normal brace (not modifiable) + assert_equal("{{{group1}}}{{{group2}}}".format(group1=group1, group2=group2), output) + # rest of delimiters, with modifications + for left, right in modifiable_delimiter_pairs.items(): + assert_equal("{left}{group1}{right}{left}{group2}{right}".format(left=left, right=right, group1=group1, group2=group2), output) + assert_equal("\\left{left}{group1}\\right{right}\\left{left}{group2}\\right{right}".format(left=left, right=right, group1=group1, group2=group2), output) + assert_equal("\\mleft{left}{group1}\\mright{right}\\mleft{left}{group2}\\mright{right}".format(left=left, right=right, group1=group1, group2=group2), output) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/lcm_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/lcm_test.py new file mode 100755 index 0000000..1e10ce5 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/lcm_test.py @@ -0,0 +1,161 @@ +from .context import assert_equal +import pytest +from sympy import Symbol, Rational, UnevaluatedExpr, lcm, ilcm, sqrt, pi + +x = Symbol('x', real=True) +y = Symbol('y', real=True) +z = Symbol('z', real=True) + + +def test_lcm_usual(): + assert_equal("\\lcm(6, 4)", lcm(6, 4)) + assert_equal("\\lcm(4, 6)", lcm(4, 6)) + assert_equal("\\lcm(2, 2)", lcm(2, 2)) + assert_equal("\\lcm(0, 21)", UnevaluatedExpr(lcm(0, 21))) + assert_equal("\\lcm(21, 0)", UnevaluatedExpr(lcm(21, 0))) + assert_equal("\\lcm(0, 0)", UnevaluatedExpr(lcm(0, 0))) + assert_equal("\\lcm(9, 21)", lcm(9, 21)) + assert_equal("\\lcm(6128, 24)", lcm(6128, 24)) + assert_equal("\\lcm(24, 6128)", lcm(24, 6128)) + assert_equal("\\lcm(1E20, 1000000)", lcm(Rational('1E20'), 1000000)) + assert_equal("\\lcm(128*10^32, 1)", lcm(Rational('128E32'), 1)) + + assert_equal("\\operatorname{lcm}(6, 4)", lcm(6, 4)) + assert_equal("\\operatorname{lcm}(4, 6)", lcm(4, 6)) + assert_equal("\\operatorname{lcm}(2, 2)", lcm(2, 2)) + assert_equal("\\operatorname{lcm}(0, 21)", UnevaluatedExpr(lcm(0, 21))) + assert_equal("\\operatorname{lcm}(21, 0)", UnevaluatedExpr(lcm(21, 0))) + assert_equal("\\operatorname{lcm}(0, 0)", UnevaluatedExpr(lcm(0, 0))) + assert_equal("\\operatorname{lcm}(9, 21)", lcm(9, 21)) + assert_equal("\\operatorname{lcm}(6128, 24)", lcm(6128, 24)) + assert_equal("\\operatorname{lcm}(24, 6128)", lcm(24, 6128)) + assert_equal("\\operatorname{lcm}(1E20, 1000000)", lcm(Rational('1E20'), 1000000)) + assert_equal("\\operatorname{lcm}(128*10^32, 1)", lcm(Rational('128E32'), 1)) + + +def test_lcm_negative(): + assert_equal("\\lcm(-12, 4)", lcm(-12, 4)) + assert_equal("\\lcm(219, -9)", lcm(219, -9)) + assert_equal("\\lcm(-8, -12)", lcm(-8, -12)) + assert_equal("\\lcm(-5, -5)", lcm(-5, -5)) + assert_equal("\\lcm(-1, 182033)", lcm(-1, 182033)) + assert_equal("\\lcm(25, -30)", lcm(25, -30)) + assert_equal("\\lcm(243, -2.9543127E21)", lcm(243, Rational('-2.9543127E21'))) + + assert_equal("\\operatorname{lcm}(-12, 4)", lcm(-12, 4)) + assert_equal("\\operatorname{lcm}(219, -9)", lcm(219, -9)) + assert_equal("\\operatorname{lcm}(-8, -12)", lcm(-8, -12)) + assert_equal("\\operatorname{lcm}(-5, -5)", lcm(-5, -5)) + assert_equal("\\operatorname{lcm}(-1, 182033)", lcm(-1, 182033)) + assert_equal("\\operatorname{lcm}(25, -30)", lcm(25, -30)) + assert_equal("\\operatorname{lcm}(243, -2.9543127E21)", lcm(243, Rational('-2.9543127E21'))) + + +def test_lcm_float(): + assert_equal("\\lcm(2.4, 3.6)", lcm(Rational('2.4'), Rational('3.6'))) + assert_equal("\\lcm(3.6, 2.4)", lcm(Rational('3.6'), Rational('2.4'))) + assert_equal("\\lcm(\\pi, 3)", lcm(pi, 3)) + assert_equal("\\lcm(618, 1.5)", lcm(618, Rational('1.5'))) + assert_equal("\\lcm(-1.5, 618)", lcm(Rational('-1.5'), 618)) + assert_equal("\\lcm(0.42, 2)", lcm(Rational('0.42'), 2)) + assert_equal("\\lcm(1.43E-13, 21)", lcm(Rational('1.43E-13'), 21)) + assert_equal("\\lcm(21, -143E-13)", lcm(21, Rational('-143E-13'))) + assert_equal("\\lcm(9.80655, 9.80655)", lcm(Rational('9.80655'), Rational('9.80655'))) + assert_equal("\\lcm(0.0000923423, -8341.234802909)", lcm(Rational('0.0000923423'), Rational('-8341.234802909'))) + assert_equal("\\lcm(\\sqrt{5}, \\sqrt{2})", lcm(sqrt(5), sqrt(2))) + + assert_equal("\\operatorname{lcm}(2.4, 3.6)", lcm(Rational('2.4'), Rational('3.6'))) + assert_equal("\\operatorname{lcm}(3.6, 2.4)", lcm(Rational('3.6'), Rational('2.4'))) + assert_equal("\\operatorname{lcm}(\\pi, 3)", lcm(pi, 3)) + assert_equal("\\operatorname{lcm}(618, 1.5)", lcm(618, Rational('1.5'))) + assert_equal("\\operatorname{lcm}(-1.5, 618)", lcm(Rational('-1.5'), 618)) + assert_equal("\\operatorname{lcm}(0.42, 2)", lcm(Rational('0.42'), 2)) + assert_equal("\\operatorname{lcm}(1.43E-13, 21)", lcm(Rational('1.43E-13'), 21)) + assert_equal("\\operatorname{lcm}(21, -143E-13)", lcm(21, Rational('-143E-13'))) + assert_equal("\\operatorname{lcm}(9.80655, 9.80655)", lcm(Rational('9.80655'), Rational('9.80655'))) + assert_equal("\\operatorname{lcm}(0.0000923423, -8341.234802909)", lcm(Rational('0.0000923423'), Rational('-8341.234802909'))) + assert_equal("\\operatorname{lcm}(\\sqrt{5}, \\sqrt{2})", lcm(sqrt(5), sqrt(2))) + + +def test_lcm_fraction(): + assert_equal("\\lcm(1/2, 3)", lcm(Rational('1/2'), 3)) + assert_equal("\\lcm(3, 1/2)", lcm(3, Rational('1/2'))) + assert_equal("\\lcm(6/2, 3)", lcm(Rational('6/2'), 3)) + assert_equal("\\lcm(1/10, 1/10)", lcm(Rational('1/10'), Rational('1/10'))) + assert_equal("\\lcm(42, 42/6)", lcm(42, Rational('42/6'))) + assert_equal("\\lcm(10000000/10, 10000)", lcm(Rational('10000000/10'), 10000)) + + assert_equal("\\operatorname{lcm}(1/2, 3)", lcm(Rational('1/2'), 3)) + assert_equal("\\operatorname{lcm}(3, 1/2)", lcm(3, Rational('1/2'))) + assert_equal("\\operatorname{lcm}(6/2, 3)", lcm(Rational('6/2'), 3)) + assert_equal("\\operatorname{lcm}(1/10, 1/10)", lcm(Rational('1/10'), Rational('1/10'))) + assert_equal("\\operatorname{lcm}(42, 42/6)", lcm(42, Rational('42/6'))) + assert_equal("\\operatorname{lcm}(10000000/10, 10000)", lcm(Rational('10000000/10'), 10000)) + + +def test_lcm_expr(): + assert_equal("\\lcm(1+1, 8)", lcm(1 + 1, 8)) + assert_equal("920*\\lcm(9, 12*4/2)", 920 * lcm(9, 12 * Rational('4/2'))) + assert_equal("\\lcm(32-128, 10)*22", lcm(32 - 128, 10) * 22) + assert_equal("\\sqrt{\\lcm(1.25E24, 1E12)}", sqrt(lcm(Rational('1.25E24'), Rational('1E12')))) + assert_equal("\\lcm(92.0, 000+2)", lcm(Rational('92.0'), 000 + 2)) + + assert_equal("\\operatorname{lcm}(1+1, 8)", lcm(1 + 1, 8)) + assert_equal("920*\\operatorname{lcm}(9, 12*4/2)", 920 * lcm(9, 12 * Rational('4/2'))) + assert_equal("\\operatorname{lcm}(32-128, 10)*22", lcm(32 - 128, 10) * 22) + assert_equal("\\sqrt{\\operatorname{lcm}(1.25E24, 1E12)}", sqrt(lcm(Rational('1.25E24'), Rational('1E12')))) + assert_equal("\\operatorname{lcm}(92.0, 000+2)", lcm(Rational('92.0'), 000 + 2)) + + +def test_lcm_symbol(): + assert_equal("\\lcm(x, y)", lcm(x, y), symbolically=True) + assert_equal("\\lcm(y, -x)", lcm(y, -x), symbolically=True) + assert_equal("\\lcm(2y, x)", lcm(2 * y, x), symbolically=True) + assert_equal("\\lcm(125, 50x)", lcm(125, 50 * x), symbolically=True) + assert_equal("\\lcm(x + 76, \\sqrt{x} * 4)", lcm(x + 76, sqrt(x) * 4), symbolically=True) + assert_equal("\\lcm(y, y)", lcm(y, y), symbolically=True) + assert_equal("y + \\lcm(0.4x, 8/3) / 2", y + lcm(Rational('0.4') * x, Rational('8/3')) / 2, symbolically=True) + assert_equal("6.673E-11 * (\\lcm(8.85418782E-12, 9x) + 4) / 8y", Rational('6.673E-11') * (lcm(Rational('8.85418782E-12'), 9 * x) + 4) / (8 * y), symbolically=True) + + assert_equal("\\operatorname{lcm}(x, y)", lcm(x, y), symbolically=True) + assert_equal("\\operatorname{lcm}(y, -x)", lcm(y, -x), symbolically=True) + assert_equal("\\operatorname{lcm}(2y, x)", lcm(2 * y, x), symbolically=True) + assert_equal("\\operatorname{lcm}(125, 50x)", lcm(125, 50 * x), symbolically=True) + assert_equal("\\operatorname{lcm}(x + 76, \\sqrt{x} * 4)", lcm(x + 76, sqrt(x) * 4), symbolically=True) + assert_equal("\\operatorname{lcm}(y, y)", lcm(y, y), symbolically=True) + assert_equal("y + \\operatorname{lcm}(0.4x, 8/3) / 2", y + lcm(Rational('0.4') * x, Rational('8/3')) / 2, symbolically=True) + assert_equal("6.673E-11 * (\\operatorname{lcm}(8.85418782E-12, 9x) + 4) / 8y", Rational('6.673E-11') * (lcm(Rational('8.85418782E-12'), 9 * x) + 4) / (8 * y), symbolically=True) + + +def test_multiple_parameters(): + assert_equal("\\lcm(830,450)", lcm(830, 450)) + assert_equal("\\lcm(6,321,429)", ilcm(6, 321, 429)) + assert_equal("\\lcm(14,2324)", lcm(14, 2324)) + assert_equal("\\lcm(3, 6, 2)", ilcm(3, 6, 2)) + assert_equal("\\lcm(8, 9, 21)", ilcm(8, 9, 21)) + assert_equal("\\lcm(144, 2988, 37116)", ilcm(144, 2988, 37116)) + assert_equal("\\lcm(144,2988,37116,18,72)", ilcm(144, 2988, 37116, 18, 72)) + assert_equal("\\lcm(144, 2988, 37116, 18, 72, 12, 6)", ilcm(144, 2988, 37116, 18, 72, 12, 6)) + assert_equal("\\lcm(32)", lcm(32, 32)) + assert_equal("\\lcm(-8, 4, -2)", lcm(-8, lcm(4, -2))) + assert_equal("\\lcm(x, y, z)", lcm(x, lcm(y, z)), symbolically=True) + assert_equal("\\lcm(6*4, 48, 3)", ilcm(6 * 4, 48, 3)) + assert_equal("\\lcm(2.4, 3.6, 0.6)", lcm(Rational('2.4'), lcm(Rational('3.6'), Rational('0.6')))) + assert_equal("\\lcm(\\sqrt{3}, \\sqrt{2},\\sqrt{100})", lcm(sqrt(3), lcm(sqrt(2), sqrt(100)))) + assert_equal("\\lcm(1E12, 1E6, 1E3, 10)", ilcm(Rational('1E12'), Rational('1E6'), Rational('1E3'), 10)) + + assert_equal("\\operatorname{lcm}(830,450)", lcm(830, 450)) + assert_equal("\\operatorname{lcm}(6,321,429)", ilcm(6, 321, 429)) + assert_equal("\\operatorname{lcm}(14,2324)", lcm(14, 2324)) + assert_equal("\\operatorname{lcm}(3, 6, 2)", ilcm(3, 6, 2)) + assert_equal("\\operatorname{lcm}(8, 9, 21)", ilcm(8, 9, 21)) + assert_equal("\\operatorname{lcm}(144, 2988, 37116)", ilcm(144, 2988, 37116)) + assert_equal("\\operatorname{lcm}(144,2988,37116,18,72)", ilcm(144, 2988, 37116, 18, 72)) + assert_equal("\\operatorname{lcm}(144, 2988, 37116, 18, 72, 12, 6)", ilcm(144, 2988, 37116, 18, 72, 12, 6)) + assert_equal("\\operatorname{lcm}(32)", lcm(32, 32)) + assert_equal("\\operatorname{lcm}(-8, 4, -2)", lcm(-8, lcm(4, -2))) + assert_equal("\\operatorname{lcm}(x, y, z)", lcm(x, lcm(y, z)), symbolically=True) + assert_equal("\\operatorname{lcm}(6*4,48, 3)", ilcm(6 * 4, 48, 3)) + assert_equal("\\operatorname{lcm}(2.4, 3.6,0.6)", lcm(Rational('2.4'), lcm(Rational('3.6'), Rational('0.6')))) + assert_equal("\\operatorname{lcm}(\\sqrt{3}, \\sqrt{2},\\sqrt{100})", lcm(sqrt(3), lcm(sqrt(2), sqrt(100)))) + assert_equal("\\operatorname{lcm}(1E12,1E6, 1E3, 10)", ilcm(Rational('1E12'), Rational('1E6'), Rational('1E3'), 10)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/left_right_cdot_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/left_right_cdot_test.py new file mode 100755 index 0000000..5533b59 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/left_right_cdot_test.py @@ -0,0 +1,9 @@ +from .context import assert_equal +import pytest +from sympy import sin, Symbol + +x = Symbol('x', real=True) + + +def test_left_right_cdot(): + assert_equal("\\sin\\left(x\\right)\\cdot x", sin(x) * x) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/linalg_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/linalg_test.py new file mode 100755 index 0000000..d6dea56 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/linalg_test.py @@ -0,0 +1,15 @@ +from .context import assert_equal +import pytest +from sympy import MatMul, Matrix + + +def test_linalg_placeholder(): + assert_equal("\\begin{pmatrix}1&2\\\\3&4\\end{pmatrix}\\cdot\\variable{v}", MatMul(Matrix([[1, 2], [3, 4]]), Matrix([1, 2])), {'v': Matrix([1, 2])}) + + +def test_linalg_placeholder_multiple(): + assert_equal("\\variable{M}\\cdot\\variable{v}", MatMul(Matrix([[1, 2], [3, 4]]), Matrix([1, 2])), {'M': Matrix([[1, 2], [3, 4]]), 'v': Matrix([1, 2])}) + + +def test_linalg_placeholder_multiple_mul(): + assert_equal("\\begin{pmatrix}3&-1\\end{pmatrix}\\cdot\\variable{M}\\cdot\\variable{v}", MatMul(Matrix([[3, -1]]), Matrix([[1, 2], [3, 4]]), Matrix([1, 2])), {'M': Matrix([[1, 2], [3, 4]]), 'v': Matrix([1, 2])}) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/max_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/max_test.py new file mode 100755 index 0000000..d359c69 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/max_test.py @@ -0,0 +1,79 @@ +from .context import assert_equal +import pytest +from sympy import Symbol, Rational, Float, Max, sqrt, exp, pi, nsimplify + +x = Symbol('x', real=True) +y = Symbol('y', real=True) +z = Symbol('z', real=True) + + +def test_max_usual(): + assert_equal("\\max(1, 5)", Max(1, 5)) + assert_equal("\\max(12, 4)", Max(12, 4)) + assert_equal("\\max(109, 120)", Max(109, 120)) + assert_equal("\\max(3, 3)", Max(3, 3)) + assert_equal("\\max(0, 0)", Max(0, 0)) + assert_equal("\\max(1)", Max(1)) + assert_equal("\\max(1092198374, 290348E32)", Max(1092198374, Rational('290348E32'))) + assert_equal("\\max(5, 2, 17, 4)", Max(5, 2, 17, 4)) + + +def test_max_negative(): + assert_equal("\\max(-9, 4)", Max(-9, 4)) + assert_equal("\\max(4, -9)", Max(4, -9)) + assert_equal("\\max(-7)", Max(-7)) + assert_equal("\\max(-2, -2)", Max(-2, -2)) + assert_equal("\\max(-324E-3, -58)", Max(Rational('-324E-3'), -58)) + assert_equal("\\max(-1, 0, 1, -37, 42)", Max(-1, 0, 1, -37, 42)) + + +def test_max_float(): + assert_equal("\\max(\\pi, 3)", Max(pi, 3)) + assert_equal("\\max(1234.56789, 1234.5678901)", Max(Rational('1234.56789'), Rational('1234.5678901'))) + assert_equal("\\max(12.4, 9.5)", Max(12.4, 9.5)) + assert_equal("\\max(6, 6.2)", Max(6, 6.2)) + assert_equal("\\max(-98.7)", Max(-98.7)) + assert_equal("\\max(7.1, 9)", Max(7.1, 9)) + assert_equal("\\max(-21E-12, 0.00005)", Max(nsimplify(Rational('-21E-12')), Rational('0.00005')), symbolically=True) + assert_equal("\\max(\\sqrt{3}, 0, 1)", Max(sqrt(3), 0, 1)) + + +def test_max_fraction(): + assert_equal("\\max(1/2, 1/4)", Max(Rational('1/2'), Rational('1/4'))) + assert_equal("\\max(6/2, 3)", Max(Rational('6/2'), 3)) + assert_equal("\\max(2/4, 1/2)", Max(Rational('2/4'), Rational('1/2'))) + assert_equal("\\max(-12/5, 6.4)", Max(Rational('-12/5'), Rational('6.4'))) + assert_equal("\\max(1/10)", Max(Rational('1/10'))) + assert_equal("\\max(1.5, \\pi/2)", Max(Rational('1.5'), pi / 2, evaluate=False)) + assert_equal("\\max(-4/3, -2/1, 0/9, -3)", Max(Rational('-4/3'), Rational('-2/1'), Rational('0/9'), -3)) + + +def test_max_expr(): + assert_equal("\\max((1+6)/3, 7)", Max(Rational(1 + 6, 3), 7)) + assert_equal("\\max(58*9)", Max(58 * 9)) + assert_equal("\\max(1+6/3, -5)", Max(1 + Rational('6/3'), -5)) + assert_equal("\\max(7*4/5, 092) * 2", Max(7 * 4 / 5, 92) * 2) + assert_equal("38+\\max(13, 15-2.3)", 38 + Max(13, 15 - Rational('2.3'))) + assert_equal("\\sqrt{\\max(99.9999999999999, 100)}", sqrt(Max(Rational('99.9999999999999'), 100))) + assert_equal("\\max(274/(5+2), \\exp(12.4), 1.4E2)", Max(Rational(274, 5 + 2), exp(Rational('12.4')), Rational('1.4E2'))) + + +def test_max_symbol(): + assert_equal("\\max(x)", Max(x), symbolically=True) + assert_equal("\\max(x, y)", Max(x, y), symbolically=True) + assert_equal("\\max(y, x)", Max(y, x), symbolically=True) + assert_equal("\\max(x+y, y+x)", Max(x + y, y + x), symbolically=True) + assert_equal("\\max(9x/4, z)", Max(9 * x / 4, z), symbolically=True) + assert_equal("\\max(y\\pi, 9)", Max(y * pi, 9), symbolically=True) + assert_equal("\\max(2y-y, y + 1)", Max(2 * y - y, y + 1), symbolically=True) + assert_equal("\\max(z, y, x)", Max(z, y, x), symbolically=True) + + +def test_max_multiarg(): + assert_equal("\\max(1,2)", Max(1, 2)) + assert_equal("\\max(9,876,543)", Max(9, 876, 543)) + assert_equal("\\max(x, y,z)", Max(x, y, z), symbolically=True) + assert_equal("\\max(5.8,7.4, 2.2,-10)", Max(Rational('5.8'), Rational('7.4'), Rational('2.2'), -10)) + assert_equal("\\max(\\pi,12E2,84,\\sqrt{5},12/5)", Max(pi, Rational('12E2'), 84, sqrt(5), Rational('12/5'))) + assert_equal("\\max(823,51)", Max(823, 51)) + assert_equal("\\max(72*4,23, 9)", Max(72 * 4, 23, 9)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/min_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/min_test.py new file mode 100755 index 0000000..f60a5cd --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/min_test.py @@ -0,0 +1,79 @@ +from .context import assert_equal +import pytest +from sympy import Symbol, Rational, Float, Min, sqrt, exp, pi, nsimplify + +x = Symbol('x', real=True) +y = Symbol('y', real=True) +z = Symbol('z', real=True) + + +def test_min_usual(): + assert_equal("\\min(1, 5)", Min(1, 5)) + assert_equal("\\min(12, 4)", Min(12, 4)) + assert_equal("\\min(109, 120)", Min(109, 120)) + assert_equal("\\min(3, 3)", Min(3, 3)) + assert_equal("\\min(0, 0)", Min(0, 0)) + assert_equal("\\min(1)", Min(1)) + assert_equal("\\min(1092198374, 290348E32)", Min(1092198374, Rational('290348E32'))) + assert_equal("\\min(5, 2, 17, 4)", Min(5, 2, 17, 4)) + + +def test_min_negative(): + assert_equal("\\min(-9, 4)", Min(-9, 4)) + assert_equal("\\min(4, -9)", Min(4, -9)) + assert_equal("\\min(-7)", Min(-7)) + assert_equal("\\min(-2, -2)", Min(-2, -2)) + assert_equal("\\min(-324E-3, -58)", Min(Rational('-324E-3'), -58)) + assert_equal("\\min(-1, 0, 1, -37, 42)", Min(-1, 0, 1, -37, 42)) + + +def test_min_float(): + assert_equal("\\min(\\pi, 3)", Min(pi, 3)) + assert_equal("\\min(1234.56789, 1234.5678901)", Min(Rational('1234.56789'), Rational('1234.5678901'))) + assert_equal("\\min(12.4, 9.5)", Min(12.4, 9.5)) + assert_equal("\\min(6, 6.2)", Min(6, 6.2)) + assert_equal("\\min(-98.7)", Min(-98.7)) + assert_equal("\\min(7.1, 9)", Min(7.1, 9)) + assert_equal("\\min(-21E-12, 0.00005)", Min(nsimplify(Rational('-21E-12')), Rational('0.00005')), symbolically=True) + assert_equal("\\min(\\sqrt{3}, 0, 1)", Min(sqrt(3), 0, 1)) + + +def test_min_fraction(): + assert_equal("\\min(1/2, 1/4)", Min(Rational('1/2'), Rational('1/4'))) + assert_equal("\\min(6/2, 3)", Min(Rational('6/2'), 3)) + assert_equal("\\min(2/4, 1/2)", Min(Rational('2/4'), Rational('1/2'))) + assert_equal("\\min(-12/5, 6.4)", Min(Rational('-12/5'), Rational('6.4'))) + assert_equal("\\min(1/10)", Min(Rational('1/10'))) + assert_equal("\\min(1.5, \\pi/2)", Min(Rational('1.5'), pi / 2, evaluate=False)) + assert_equal("\\min(-4/3, -2/1, 0/9, -3)", Min(Rational('-4/3'), Rational('-2/1'), Rational('0/9'), -3)) + + +def test_min_expr(): + assert_equal("\\min((1+6)/3, 7)", Min(Rational(1 + 6, 3), 7)) + assert_equal("\\min(58*9)", Min(58 * 9)) + assert_equal("\\min(1+6/3, -5)", Min(1 + Rational('6/3'), -5)) + assert_equal("\\min(7*4/5, 092) * 2", Min(7 * 4 / 5, 92) * 2) + assert_equal("38+\\min(13, 15-2.3)", 38 + Min(13, 15 - Rational('2.3'))) + assert_equal("\\sqrt{\\min(99.9999999999999, 100)}", sqrt(Min(Rational('99.9999999999999'), 100))) + assert_equal("\\min(274/(5+2), \\exp(12.4), 1.4E2)", Min(Rational(274, 5 + 2), exp(Rational('12.4')), Rational('1.4E2'))) + + +def test_min_symbol(): + assert_equal("\\min(x)", Min(x), symbolically=True) + assert_equal("\\min(x, y)", Min(x, y), symbolically=True) + assert_equal("\\min(y, x)", Min(y, x), symbolically=True) + assert_equal("\\min(x+y, y+x)", Min(x + y, y + x), symbolically=True) + assert_equal("\\min(9x/4, z)", Min(9 * x / 4, z), symbolically=True) + assert_equal("\\min(y\\pi, 9)", Min(y * pi, 9), symbolically=True) + assert_equal("\\min(2y-y, y + 1)", Min(2 * y - y, y + 1), symbolically=True) + assert_equal("\\min(z, y, x)", Min(z, y, x), symbolically=True) + + +def test_min_multiarg(): + assert_equal("\\min(1,2)", Min(1, 2)) + assert_equal("\\min(9,876,543)", Min(9, 876, 543)) + assert_equal("\\min(x, y,z)", Min(x, y, z), symbolically=True) + assert_equal("\\min(5.8,7.4, 2.2,-10)", Min(Rational('5.8'), Rational('7.4'), Rational('2.2'), -10)) + assert_equal("\\min(\\pi,12E2,84,\\sqrt{5},12/5)", Min(pi, Rational('12E2'), 84, sqrt(5), Rational('12/5'))) + assert_equal("\\min(823,51)", Min(823, 51)) + assert_equal("\\min(72*4,23, 9)", Min(72 * 4, 23, 9)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/mod_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/mod_test.py new file mode 100755 index 0000000..972fe7a --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/mod_test.py @@ -0,0 +1,70 @@ +from .context import assert_equal +import pytest +from sympy import Symbol, Rational, Mod, sqrt, nsimplify, pi, GoldenRatio +from sympy.physics.units import hbar + +x = Symbol('x', real=True) +y = Symbol('y', real=True) + + +def test_mod_usual(): + assert_equal("128\\mod 3", Mod(128, 3)) + assert_equal("7\\mod 128", Mod(7, 128)) + assert_equal("5\\mod 10", Mod(5, 10)) + assert_equal("5\\mod 5", Mod(5, 5)) + assert_equal("3\\mod 2", Mod(3, 2)) + assert_equal("0 \\mod 6", Mod(0, 6)) + assert_equal("6109\\mod 28", Mod(6109, 28)) + assert_equal("4000000000\\mod 28791", Mod(4000000000, 28791)) + assert_equal("128*10^300\\mod 876123", Mod(Rational('128E300'), 876123)) + assert_equal("876,123\\mod 128E300)", Mod(876123, Rational('128E300'))) + + +def test_mod_negative(): + assert_equal("-1\\mod 2", Mod(-1, 2)) + assert_equal("-3\\mod 3", Mod(-3, 3)) + assert_equal("-12\\mod -12", Mod(-12, -12)) + assert_equal("-128\\mod 4", Mod(-128, 4)) + assert_equal("9\\mod -213", Mod(9, -213)) + assert_equal("123123\\mod -541", Mod(123123, -541)) + assert_equal("-123123\\mod 541", Mod(-123123, 541)) + assert_equal("-97E34\\mod 7", Mod(Rational('-97E34'), 7)) + + +def test_mod_fraction(): + assert_equal("1/2\\mod 3", Mod(Rational(1, 2), 3)) + assert_equal("6/2\\mod 3", Mod(Rational(6, 2), 3)) + assert_equal("-14/2\\mod 5", Mod(Rational(-14, 2), 5)) + assert_equal("123\\mod (42/6)", Mod(123, Rational(42, 6))) + assert_equal("431\\mod (2/123)", Mod(431, Rational(2, 123))) + assert_equal("5/5\\mod (5/5)", Mod(Rational(5, 5), Rational(5, 5))) + assert_equal("849/-21\\mod (092/2)", Mod(Rational(849, -21), Rational(92, 2))) + assert_equal("13*10^9\\mod (21/-2)", Mod(13E9, Rational(21, -2))) + + +def test_mod_float(): + assert_equal("0.41\\mod 2", Mod(Rational('0.41'), 2)) + assert_equal("143E-13\\mod 21", Mod(Rational('143E-13'), 21)) + assert_equal("-9.80665\\mod 9.80665", Mod(-9.80665, 9.80665)) + assert_equal("0.0000923423\\mod -8341.234802909", nsimplify(Mod(0.0000923423, -8341.234802909))) + assert_equal("\\sqrt{5}\\mod \\sqrt{2}", Mod(sqrt(5), sqrt(2))) + assert_equal("987\\mod \\pi", Mod(987, pi)) + assert_equal("\\pi\\mod ((1+\\sqrt{5})/2)", Mod(pi, nsimplify(GoldenRatio)), symbolically=True) + assert_equal("1234\\mod 1E-29", Mod(1234, Rational('1E-29'), evaluate=False)) + + +def test_mod_expr(): + assert_equal("1+1\\mod 2", 1 + Mod(1, 2)) + assert_equal("876123\\mod 128\\times 10^300", Mod(876123, 128) * 1E300) + assert_equal("141\\mod 9/3", Rational(Mod(141, 9) / 3)) + assert_equal("872 / (12\\mod 9 * 4) * 2", Rational(2 * 872, (Mod(12, 9) * 4))) + assert_equal("1E-32 * (1E29\\mod 74)", Rational('1E-32') * Mod(Rational('1E29'), 74)) + assert_equal("299,792,458\\mod 9.81", Mod(299792458, Rational('9.81'))) + + +def test_mod_symbol(): + assert_equal("x\\mod y", Mod(x, y)) + assert_equal("2x\\mod y", Mod(2 * x, y)) + assert_equal("y + 3\\mod 2 / 4", y + Rational(Mod(3, 2), 4), symbolically=True) + assert_equal("0.5x * 2 + \\sqrt{x}\\mod 8y", 0.5 * x * 2 + Mod(sqrt(x), 8 * y), symbolically=True) + assert_equal("6.673E-11 * ((8.85418782E-12\\mod 9x) + 4) / 2y", Rational('6.673E-11') * (Mod(Rational('8.85418782E-12'), 9 * x) + 4) / (2 * y), symbolically=True) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/overline_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/overline_test.py new file mode 100755 index 0000000..a75103e --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/overline_test.py @@ -0,0 +1,9 @@ +from .context import assert_equal +import pytest +from sympy import sin, Symbol + +x = Symbol('x', real=True) + + +def test_overline(): + assert_equal("\\frac{\\sin(x)}{\\overline{x}_n}", sin(x) / Symbol('xbar_n', real=True)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/pi_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/pi_test.py new file mode 100755 index 0000000..050190d --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/pi_test.py @@ -0,0 +1,15 @@ +from .context import assert_equal, _Mul, _Pow +import pytest +from sympy import pi, Symbol, acos, cos + + +def test_pi_frac(): + assert_equal("\\frac{\\pi}{3}", _Mul(pi, _Pow(3, -1))) + + +def test_pi_nested(): + assert_equal("\\arccos{\\cos{\\frac{\\pi}{3}}}", acos(cos(_Mul(pi, _Pow(3, -1)), evaluate=False), evaluate=False)) + + +def test_pi_arccos(): + assert_equal("\\arccos{-1}", pi, symbolically=True) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/trig_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/trig_test.py new file mode 100755 index 0000000..4689ea5 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/trig_test.py @@ -0,0 +1,21 @@ +from .context import assert_equal +import pytest +from sympy import asinh, Symbol + +# x = Symbol('x', real=True); + +# latex = "\\sinh(x)" +# math = process_sympy(latex) +# print("latex: %s to math: %s" %(latex,math)) +# +# latex = "\\arcsinh(x)" +# math = process_sympy(latex) +# print("latex: %s to math: %s" %(latex,math)) +# +# latex = "\\arsinh(x)" +# math = process_sympy(latex) +# print("latex: %s to math: %s" %(latex,math)) + + +def test_arcsinh(): + assert_equal("\\operatorname{arcsinh}\\left(1\\right)", asinh(1, evaluate=False)) diff --git a/Qwen2.5-Eval/evaluation/latex2sympy/tests/variable_test.py b/Qwen2.5-Eval/evaluation/latex2sympy/tests/variable_test.py new file mode 100755 index 0000000..9fc13c7 --- /dev/null +++ b/Qwen2.5-Eval/evaluation/latex2sympy/tests/variable_test.py @@ -0,0 +1,92 @@ +from .context import assert_equal +import pytest +import hashlib +from sympy import UnevaluatedExpr, Symbol, Mul, Pow, Max, Min, gcd, lcm, floor, ceiling + +x = Symbol('x', real=True) +y = Symbol('y', real=True) + + +def test_variable_letter(): + assert_equal("\\variable{x}", Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True)) + + +def test_variable_digit(): + assert_equal("\\variable{1}", Symbol('1' + hashlib.md5('1'.encode()).hexdigest(), real=True)) + + +def test_variable_letter_subscript(): + assert_equal("\\variable{x_y}", Symbol('x_y' + hashlib.md5('x_y'.encode()).hexdigest(), real=True)) + + +def test_variable_letter_comma_subscript(): + assert_equal("\\variable{x_{i,j}}", Symbol('x_{i,j}' + hashlib.md5('x_{i,j}'.encode()).hexdigest(), real=True)) + + +def test_variable_digit_subscript(): + assert_equal("\\variable{x_1}", Symbol('x_1' + hashlib.md5('x_1'.encode()).hexdigest(), real=True)) + + +def test_variable_after_subscript_required(): + with pytest.raises(Exception): + assert_equal("\\variable{x_}", Symbol('x_' + hashlib.md5('x_'.encode()).hexdigest(), real=True)) + + +def test_variable_before_subscript_required(): + with pytest.raises(Exception): + assert_equal("\\variable{_x}", Symbol('_x' + hashlib.md5('_x'.encode()).hexdigest(), real=True)) + + +def test_variable_bad_name(): + with pytest.raises(Exception): + assert_equal("\\variable{\\sin xy}", None) + + +def test_variable_in_expr(): + assert_equal("4\\cdot\\variable{x}", 4 * Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True)) + + +def test_variable_greek_letter(): + assert_equal("\\variable{\\alpha }\\alpha", Symbol('\\alpha ' + hashlib.md5('\\alpha '.encode()).hexdigest(), real=True) * Symbol('alpha', real=True)) + + +def test_variable_greek_letter_subscript(): + assert_equal("\\variable{\\alpha _{\\beta }}\\alpha ", Symbol('\\alpha _{\\beta }' + hashlib.md5('\\alpha _{\\beta }'.encode()).hexdigest(), real=True) * Symbol('alpha', real=True)) + + +def test_variable_bad_unbraced_long_subscript(): + with pytest.raises(Exception): + assert_equal("\\variable{x_yz}", None) + + +def test_variable_bad_unbraced_long_complex_subscript(): + with pytest.raises(Exception): + assert_equal("\\variable{x\\beta 10_y\\alpha 20}", None) + + +def test_variable_braced_subscript(): + assert_equal("\\variable{x\\beta 10_{y\\alpha 20}}", Symbol('x\\beta 10_{y\\alpha 20}' + hashlib.md5('x\\beta 10_{y\\alpha 20}'.encode()).hexdigest(), real=True)) + + +def test_variable_complex_expr(): + assert_equal("4\\cdot\\variable{value1}\\frac{\\variable{value_2}}{\\variable{a}}\\cdot x^2", 4 * Symbol('value1' + hashlib.md5('value1'.encode()).hexdigest(), real=True) * Symbol('value_2' + hashlib.md5('value_2'.encode()).hexdigest(), real=True) / Symbol('a' + hashlib.md5('a'.encode()).hexdigest(), real=True) * x**2) + + +def test_variable_dollars(): + assert_equal("\\$\\variable{x}", Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True)) + + +def test_variable_percentage(): + assert_equal("\\variable{x}\\%", Mul(Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True), Pow(100, -1, evaluate=False), evaluate=False)) + + +def test_variable_single_arg_func(): + assert_equal("\\floor(\\variable{x})", floor(Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True))) + assert_equal("\\ceil(\\variable{x})", ceiling(Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True))) + + +def test_variable_multi_arg_func(): + assert_equal("\\gcd(\\variable{x}, \\variable{y})", UnevaluatedExpr(gcd(Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True), Symbol('y' + hashlib.md5('y'.encode()).hexdigest(), real=True)))) + assert_equal("\\lcm(\\variable{x}, \\variable{y})", UnevaluatedExpr(lcm(Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True), Symbol('y' + hashlib.md5('y'.encode()).hexdigest(), real=True)))) + assert_equal("\\max(\\variable{x}, \\variable{y})", Max(Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True), Symbol('y' + hashlib.md5('y'.encode()).hexdigest(), real=True), evaluate=False)) + assert_equal("\\min(\\variable{x}, \\variable{y})", Min(Symbol('x' + hashlib.md5('x'.encode()).hexdigest(), real=True), Symbol('y' + hashlib.md5('y'.encode()).hexdigest(), real=True), evaluate=False)) |
